原文信息

https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=7192717

Reducing Snapshots to Points: A Visual Analytics Approach to Dynamic Network Exploration
Stef van den Elzen, Danny Holten, Jorik Blaas, Jarke J. van Wijk
IEEE TRANSACTIONS ON VISUALIZATION AND COMPUTER GRAPHICS, VOL. 22, NO. 1, JANUARY 2016

获得 IEEE VIS 2015 VAST 最佳论文

概述

文章提出了一种动态时序网络的可视交互分析方法。把每个时间点或时间区间的网络快照作为一个在高维空间中的节点，将这些节点投影到二维空间当中，并同时提供单个快照的视图和网络变革的视图来进行交互。通过这种方法，用户可以发现网络变革过程中的稳定状态，循环状态，离群状态，并得到状态转换和网络的全局演变等。此方法主要通过离散化，向量化，正则化，降维，可视化和交互这几个部分进行。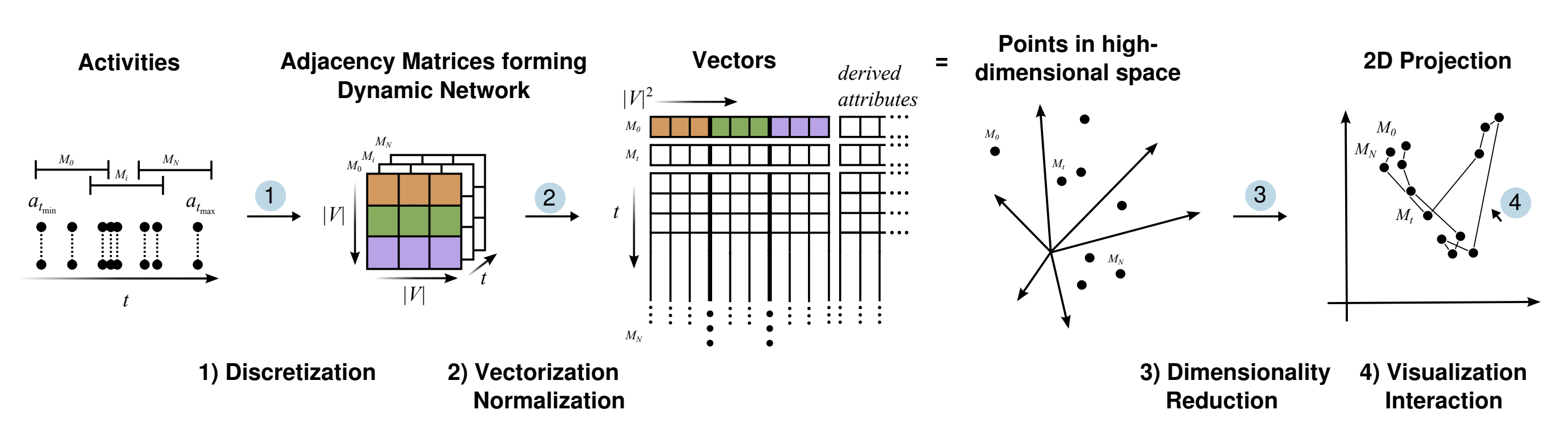

算法

将网络快照降维成节点

可视分析方法

首先设一个动态网络模型 Γ，它有 N 个快照：

每个快照是一个有向图 ，所有快照中的边形成的并集是 E :

动态网络离散化

动态网络的快照是指动态网络在某个序列点（或一小阶段）的网络图结构。
在实际生活中，存在时间序列的事件组成的数据集是十分普遍的。这类数据的活动日志可以被模拟成：
，
每个 是一个活动，它由边 和时间戳 组成。假设 代表一个时间点，并且 是等距的，代表了一天，一小时，或者是一分钟等。每个时间窗口 的宽度为 。这个时间窗中的边集合为：

每条边 e 具有权重 ，是 Aj 中所含边的数量。

快照向量化和正则化

每一个快照可以被表达成 |V|*|V| 的邻接矩阵，将每个矩阵拼接成一个 的行向量。总共有 N 个快照，将 N 个 的行向量组成一个 的矩阵。这个矩阵的每一列表示一条边在动态网络中的变化情况，而每一行则表示了一个快照。将每一列看作一个特征向量，表达了一条边随时间变化的行为。
为了在下一步数据降维中得到更好的降维结果，首先将矩阵进行正则化。文中使用了三种方法：binarization, min-max, 和 z-score 。

高维数据降维

将所有快照进行高维数据将为并投影到二维空间当中。文中使用了几个线性和非线性的降维方法。例如 PCA ， MDS ，t-SNE 等。

可视化及交互

所有快照的投影视图和一个被选中的快照的详细网络可视化。

应用场景

高校内部联络模式分析

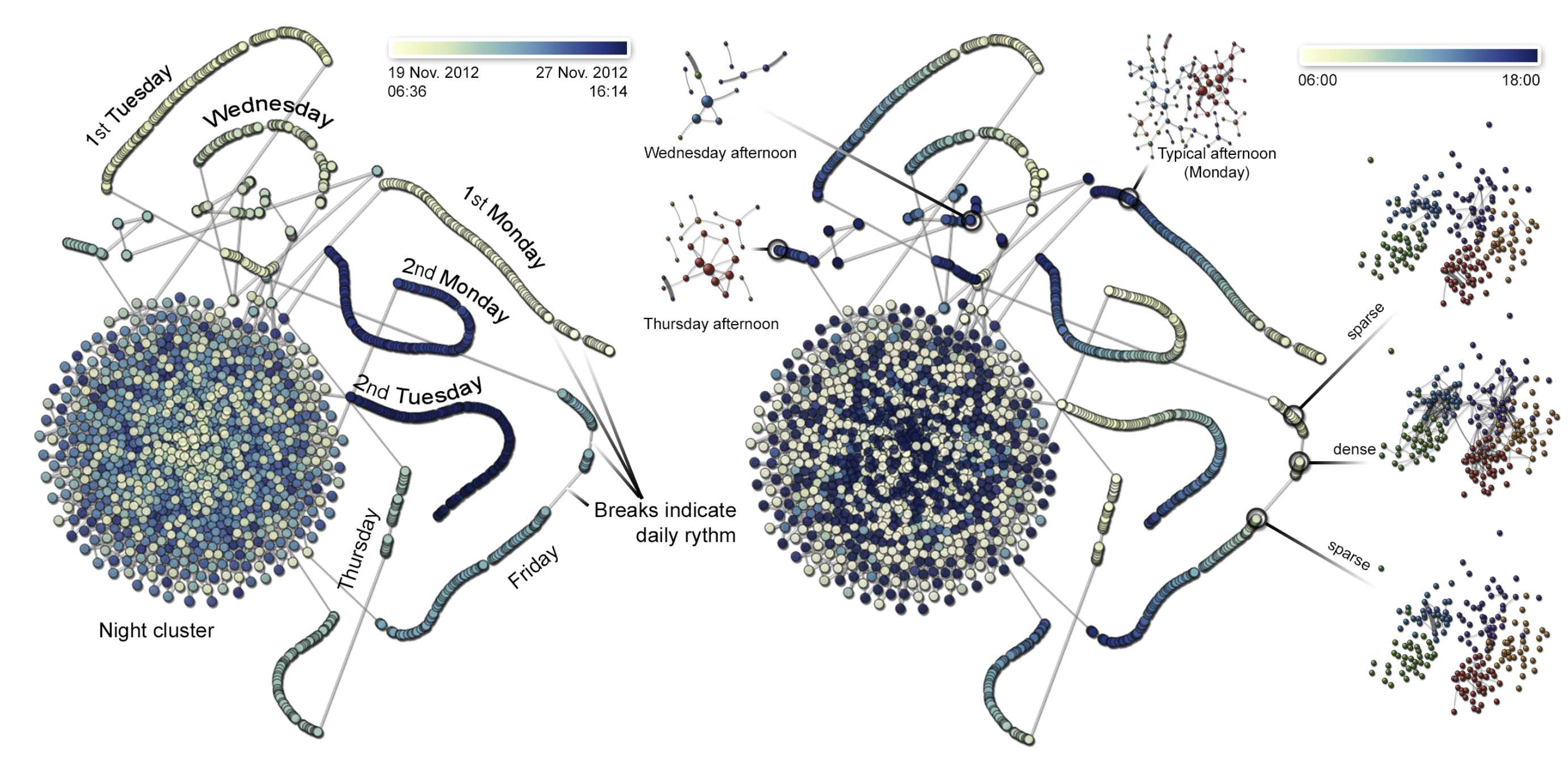
在每一个快照中，节点代表学生（180人），边代表两个学生之间的面对面接触。一个快照代表了每 60 分钟的学生接触情况。在下图的结果中，颜色代表了日期。左右两个结果是使用了不同的正则化方法。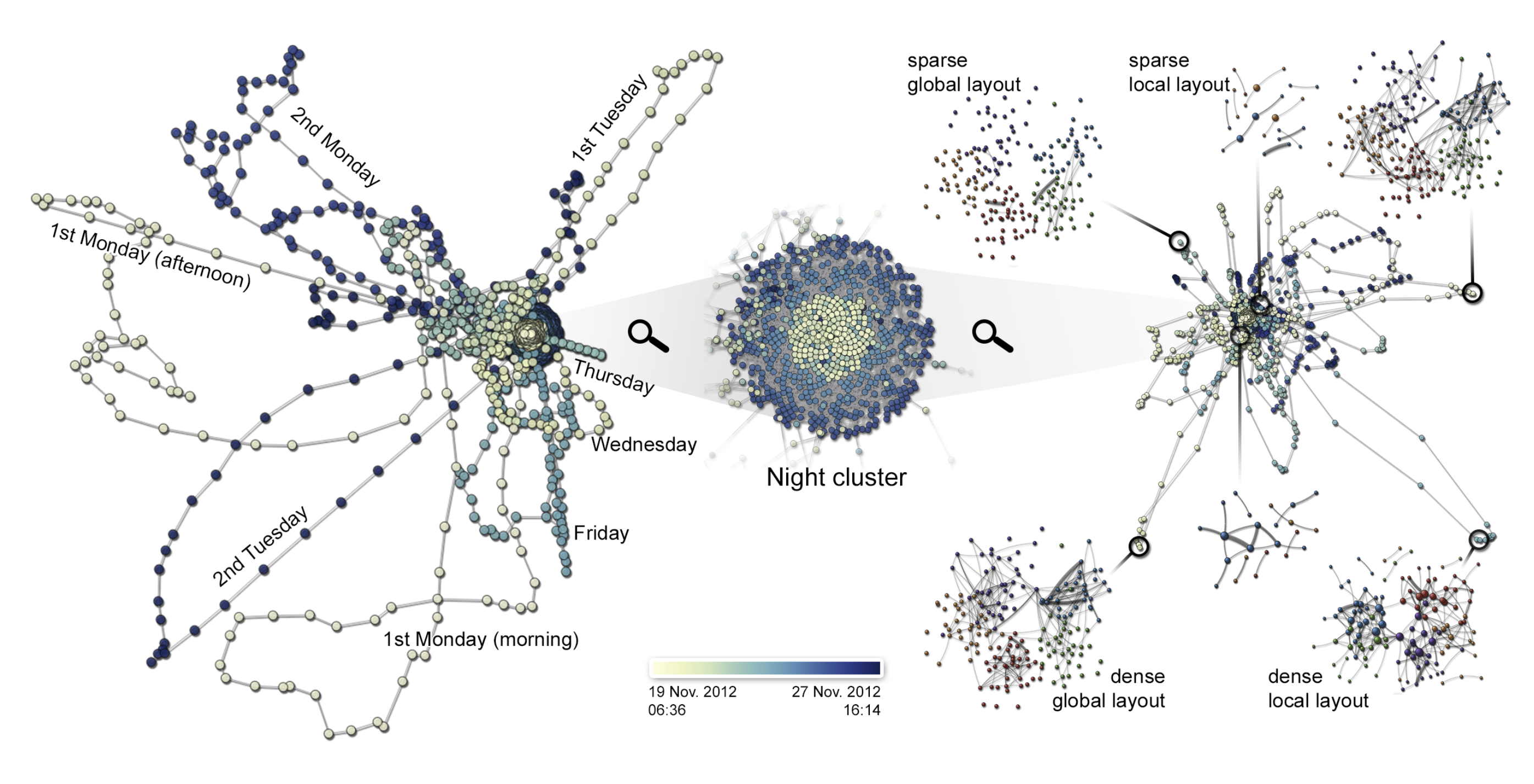

颜色代表了日期（左）和小时（右）：