内含各种论文和算法，阅读起来较为费力。

适读人群：对Dagre内部实现原理有兴趣的同学，或者有基于Dagre二次开发的需求。 阅读时长：1小时。

一、前言

常见的图可视化布局算法有：Dagre布局、Sankey布局、力导布局、随机布局等。
由于近期业务中需要，几种布局算法中，Dagre布局最能贴近业务需求，但同时也需要有一些定制能力。所以花时间研究了下Dagre布局的源码部分，以及其中涉及到的论文部分。
有部分算法的理解可能不是很透彻，欢迎大家交流。

二、核心步骤

源码地址：https://github.com/dagrejs/dagre
算法核心：布局算法的核心函数如下。
建议：在直接看源码之前，建议大家可以先大概看一下《A Technique for Drawing Directed Graphs》这篇论文，论文中讲述的是有向图的一种布局算法。Dagre的大体思路和步骤和论文中讲述的差不多，只是在每一步的具体实现上会有些差异点。

  1. function runLayout(g, time) {
  2.   // 优化边上label的位置
  3.   time("    makeSpaceForEdgeLabels", function() { makeSpaceForEdgeLabels(g); });
  4.   // 去除自环
  5.   time("    removeSelfEdges",        function() { removeSelfEdges(g); });
  6.   // 去环
  7.   time("    acyclic",                function() { acyclic.run(g); });
  8.   // 复合图布局，复合图生成虚拟节点，并排序成nesting graph
  9.   time("    nestingGraph.run",       function() { nestingGraph.run(g); });
  10.   // 层级分配
  11.   time("    rank",                   function() { rank(util.asNonCompoundGraph(g)); });
  12.   // 边lable的处理。在边的中间位置生成虚拟节点，代表lable的位置
  13.   time("    injectEdgeLabelProxies", function() { injectEdgeLabelProxies(g); });
  14.   // 移除空的层级，并将rank都调整为正数
  15.   time("    removeEmptyRanks",       function() { removeEmptyRanks(g); });
  16.   // 移除虚拟边和虚拟根节点
  17.   time("    nestingGraph.cleanup",   function() { nestingGraph.cleanup(g); });
  18.   // 调整rank为>=0的数
  19.   time("    normalizeRanks",         function() { normalizeRanks(g); });
  20.   // 找到节点组的最大和最小层级
  21.   time("    assignRankMinMax",       function() { assignRankMinMax(g); });
  22.   // 移除边的label虚节点，将虚节点的层级记录到label对象中
  23.   time("    removeEdgeLabelProxies", function() { removeEdgeLabelProxies(g); });
  24.   // 将长度大于1的边，分割成长度为1的n条边，并在边中插入虚拟节点
  25.   time("    normalize.run",          function() { normalize.run(g); });
  26.   time("    parentDummyChains",      function() { parentDummyChains(g); });
  27.   // 给组添加边框，增加左侧虚节点和右侧虚节点
  28.   time("    addBorderSegments",      function() { addBorderSegments(g); });
  29.   // 节点排序
  30.   time("    order",                  function() { order(g); });
  31.   // 回填自环路
  32.   time("    insertSelfEdges",        function() { insertSelfEdges(g); });
  33.   // 调整坐标系，默认是按照上下布局来算的，如果是左右布局，就对调节点和图的width和height
  34.   time("    adjustCoordinateSystem", function() { coordinateSystem.adjust(g); });
  35.   // 布局，计算位置
  36.   time("    position",               function() { position(g); });
  37.   time("    positionSelfEdges",      function() { positionSelfEdges(g); });
  38.   // 根据group的虚节点，计算group的位置，然后移除虚节点
  39.   time("    removeBorderNodes",      function() { removeBorderNodes(g); });
  40.   // 移除前面长边切割中插入的虚拟节点
  41.   time("    normalize.undo",         function() { normalize.undo(g); });
  42.   // 边的label
  43.   time("    fixupEdgeLabelCoords",   function() { fixupEdgeLabelCoords(g); });
  44.   // 根据布局方向，调整节点和边的宽度、高度，以及xy坐标
  45.   time("    undoCoordinateSystem",   function() { coordinateSystem.undo(g); });
  46.   // 算出x，y坐标
  47.   time("    translateGraph",         function() { translateGraph(g); });
  48.   // 计算边的point坐标轴
  49.   time("    assignNodeIntersects",   function() { assignNodeIntersects(g); });
  50.   // 反转反转边
  51.   time("    reversePoints",          function() { reversePointsForReversedEdges(g); });
  52.   time("    acyclic.undo",           function() { acyclic.undo(g); });
  53. }

总共是23步，其中有很多数据转换和处理的部分。
布局最核心的是四个阶段：
第一阶段：去环。
第二阶段：层级划分。
第三阶段：同层级内节点排序。
第四阶段：绘图
下面分别描述四个阶段的具体算法和细节。

三、去环算法

由于环路的存在，会影响层级分配的稳定性，所以在层级分配之前，需要先去环。
Dagre中提供了两种去环算法：DFS去环算法、贪心算法

1. DFS去环算法

算法核心

每个节点从自己的每条出边开始深度优先遍历，如果出边e1的遍历路径中不存在当前节点，说明当前链路不存在环路。如果出边e1的遍历路径中存在当前节点，则说明存在环。通过去掉最后环路的最后一条边，达到去环的效果。

时间复杂度

深入解读Dagre布局算法 - 图1

2. 贪心算法

参考论文

Dagre中贪心算法的实现参考了论文《A FAST & EFFECTIVE HEURISTIC FOR THE FEEDBACK ARC SET PROBLEM》。

算法核心

优先反转那些同时存在于多个环路中的边，尽可能的少反转边。
对于给定的一张图，按照一定顺序从左到右排列节点，使得边的方向尽量是从左到右的，那么从右到左的边则成为可能形成环路的边，即为需要反转的边。从而将求最少反转环的问题，转换成求一个节点序列。
以下为求节点序列的算法伪代码。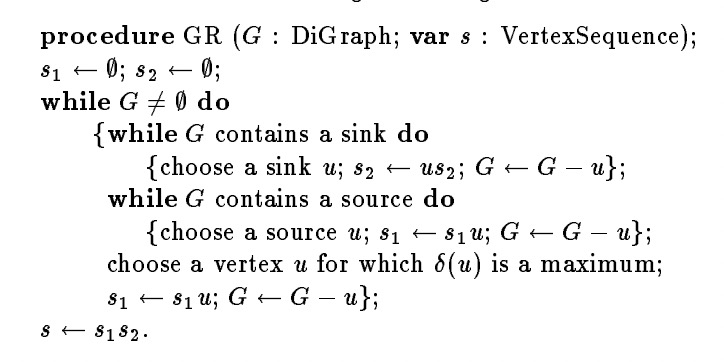
image.png

时间复杂度

深入解读Dagre布局算法 - 图3, m为边的个数

示例

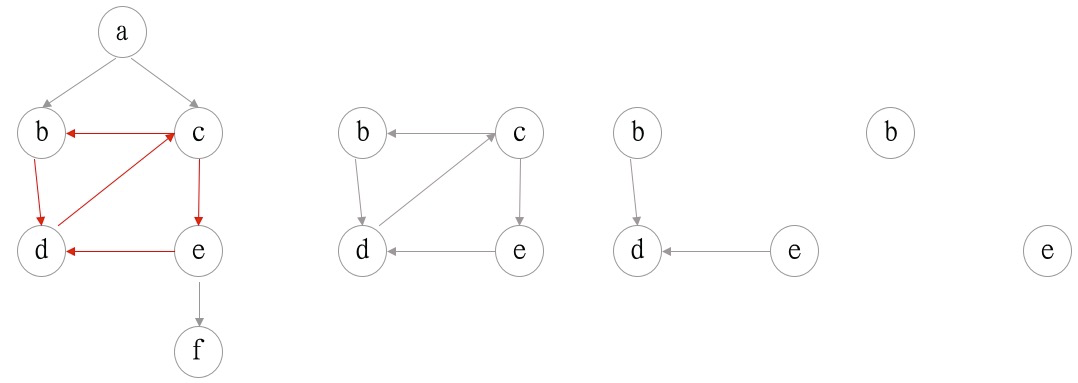
image.png
图中存在两个环，分别为b->d->c, d->c->e。按照上述算法思路，对节点进行排序

  1. 初始状态：s1=[], s2=[], s=[], G=a,b,c,d,e,f
  2. 叶子节点f，放入s2，并从图中移除。 s2=[f]
  3. 根节点a，放入s1，并从图中移除，s1=[a],并从图中移除，如图2
  4. 选取一个节点（出度-入度）最大的，即节点c。
  5. 将节点c加入到s1的末尾，并从图中移除，此时s1=[a,c]，如图3
  6. 将叶子节点d放入s2，s2=[d,f]，图中移除d。
  7. 将根节点b,e放入s1，s1=[a,c,b,e]。
  8. 图为空，结束。
  9. s=[a,c,b,e,d,f].

根据得到的序列，重新从左到右绘制图。如下图：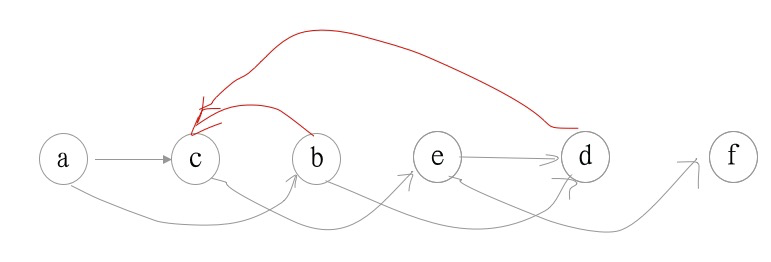
image.png

Dagre的做法：逆转第一个出度-入度 max节点的入边。即在上述步骤3的时候，就移除了d->c.

四、层级分配

输入条件：图必须是一个连通图、边均含有minlen和weight两个属性。（其中minlen表示边的长度，weight表示边的权重。）
返回结果：图中的节点都会有一个rank属性表示其所在层级。
Dagre中实现了三种层级分配算法：最长路径、紧致树、network-simplex三种。

1. 最长路径算法

算法核心

前提条件：图必须是一个有向无环图
返回结果：每一个节点都有rank属性。
尽可能多的把节点置于最底层。

时间复杂度

深入解读Dagre布局算法 - 图6，n为图中节点个数。

最长路径算法是最快最简单的，但其效果不好，会导致很多长边的存在。但是因为这种算法速度快，所以也通常会用来当做其他算法的预处理步骤，计算一个初始的层级。

示例

image.png

2. 紧致树算法

算法核心

先用最长路径算出初始层级，然后调整松弛边的长度，松弛度的定义是相对于边的minlen。
松弛边定义：边的长度大于其实际所需长度。即松弛度 > minlen。
用最长路径算法舒适分层后，紧接着进行去松弛边，伪代码：
image.png

  1. 定义边的松弛度为（边长-边的minlen）。
  2. 把目前已经紧致的节点添加到tightTree中，然后从松弛度最小的边开始逐步处理。
  3. 如果松弛边的源节点在tightTree，将边的目标节点层级向上移动delta；
  4. 如果松弛边的源节点不在tightTree，将边的源节点层级向下移动delta；
  5. 直至所有的节点都被加到tightTree中。

    时间复杂度

    深入解读Dagre布局算法 - 图9，n为图中节点个数。

    示例

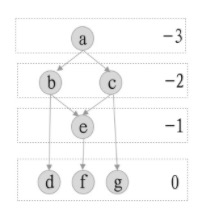
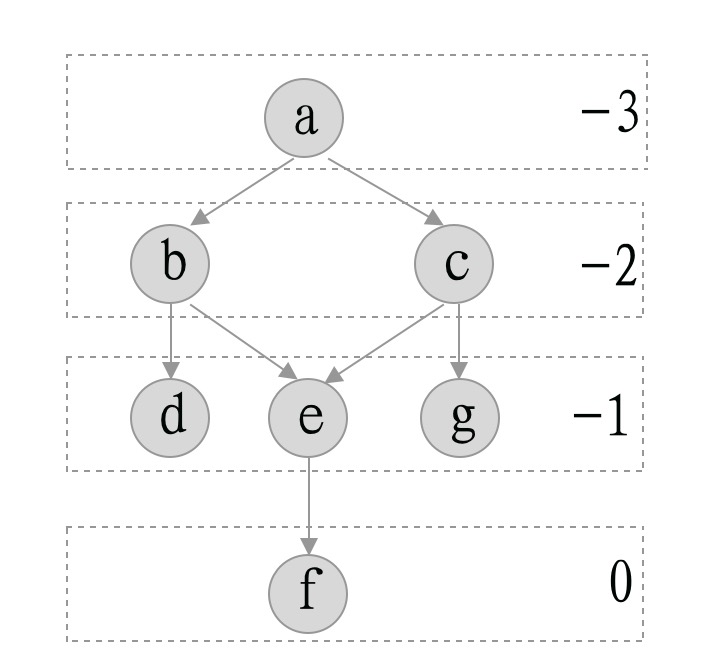
    image.png image.png

3. networks simplex算法

参考论文

《A Technique for Drawing Directed Graphs》

核心思想

迭代修改节点的层级，缩小松弛边。

  1. 先将图中紧致的边及其相关的节点加入到树中，构建一颗紧致生成树。（生成紧致树的算法使用上面的紧致树算法）
  2. 分配给起始节点一个层级，然后从起始节点出发，找到邻近的节点，然后根据其与起始节点的上下游关系，计算连通边的最小长度。
  3. 直到所有的节点都有一个默认层级。
  4. 计算每条边的切割值。切割值的计算：移除该边，将生成树分为两个区域，根据边的方向，分为头部区域v和尾部区域w，那么该边的切割值就等于，尾部区域w到 头部区域v的所有连接边的weight之和（注如果边的方向是从头部到尾部的，那么该边的weight即为负值）。

如针对下图，其最小紧致生成树为去掉虚线边的部分。
则边e的其切割值为：从v到w的边为1条，从w到v的边为2条。因此其切割值为-1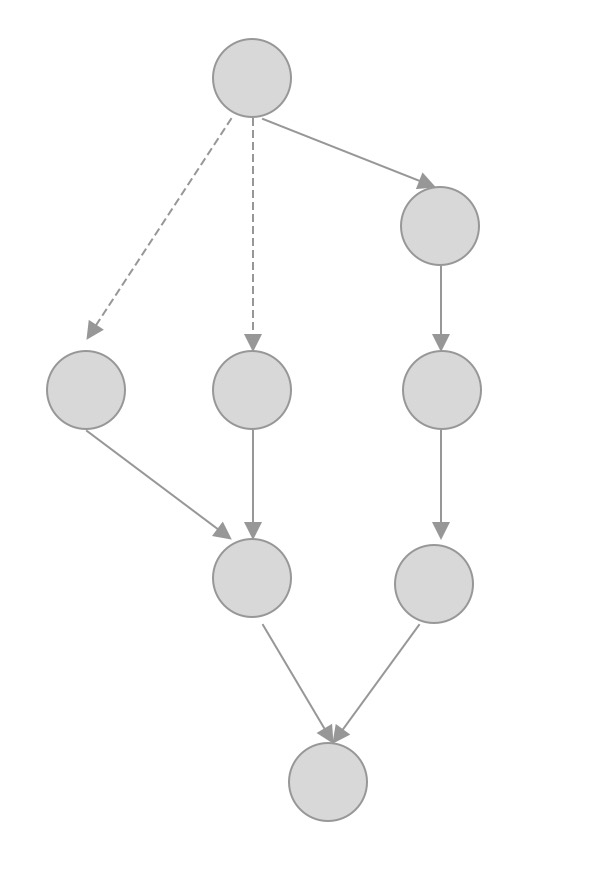
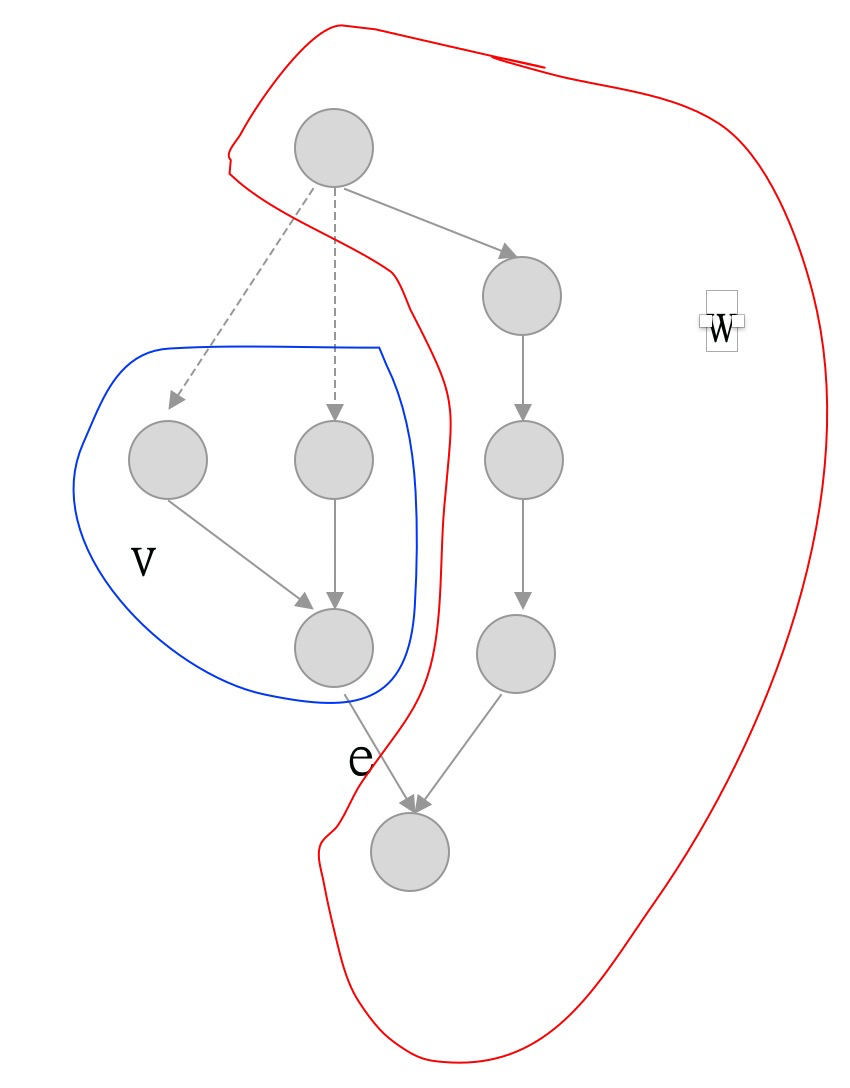
image.pngimage.png

  1. 切割值为负的边，即为需要调整的边。调整方式：加长该边的长度。
  2. 替换生成树的边，构成新的生成树。
  3. 根据新的生成树，重新调整层级。
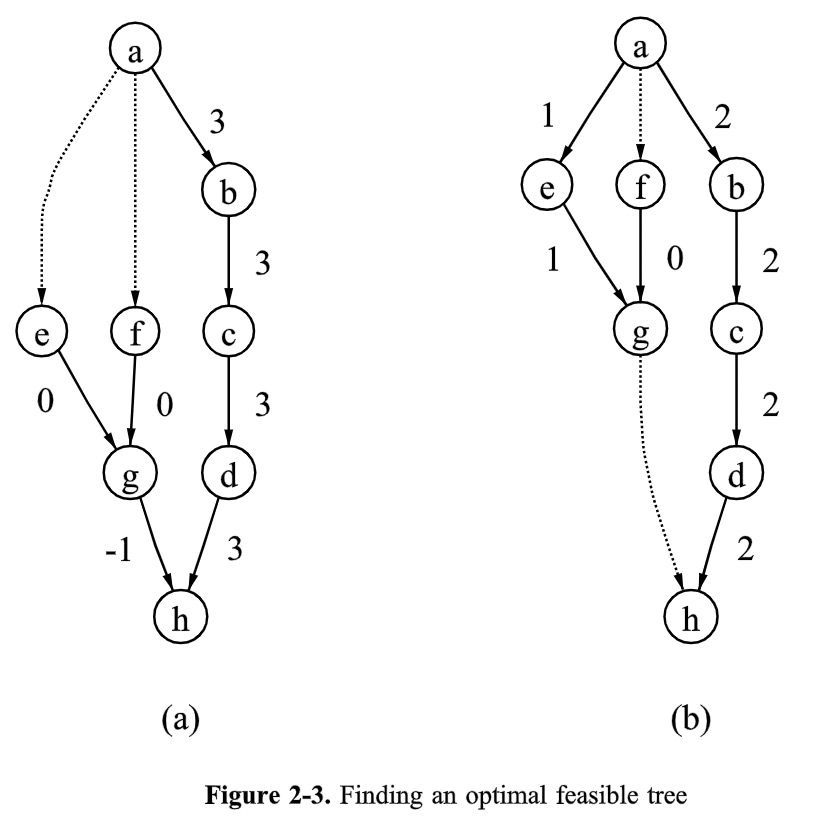
    1. procedure rank（）
    2.  feasible_tree();
    3.  while (e=leave_edge(e)) != nil do
    4.      f = enter_edge(e);
    5.      exchange(e,f);
    6.  end;
    7.  normalize();
    8.  balance();
    9. end

    示例

    image.png

    算法优化

    上述算法步骤中其中生成紧致生成树和初始的切割值耗时较大，复杂度深入解读Dagre布局算法 - 图15。论文中针对这两个步骤又分别提出了优化的解法。
    1）生成初始切割值优化
    思路：选取生成树的叶子节点，计算该节点的边的切割值。对于非叶子节点的切割值，可以根据已有边的切割值算出。
    验证：下图中，u,v,w,x四个节点之间有三条边，三条边的切割值深入解读Dagre布局算法 - 图16满足下面的计算公式
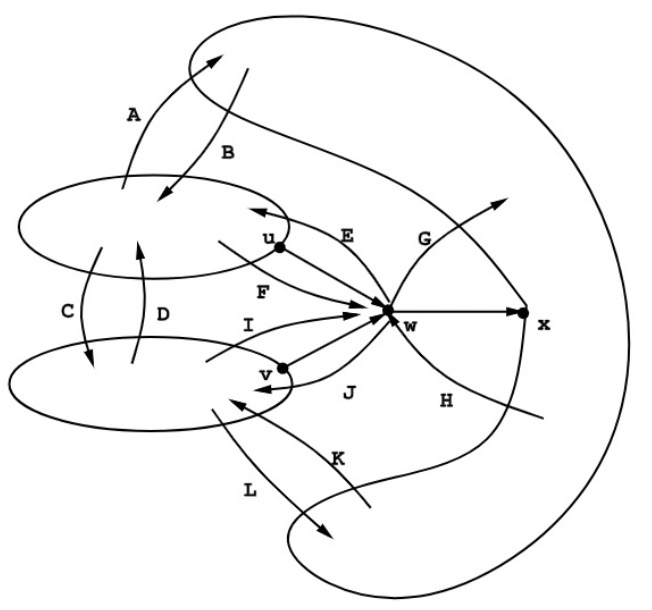
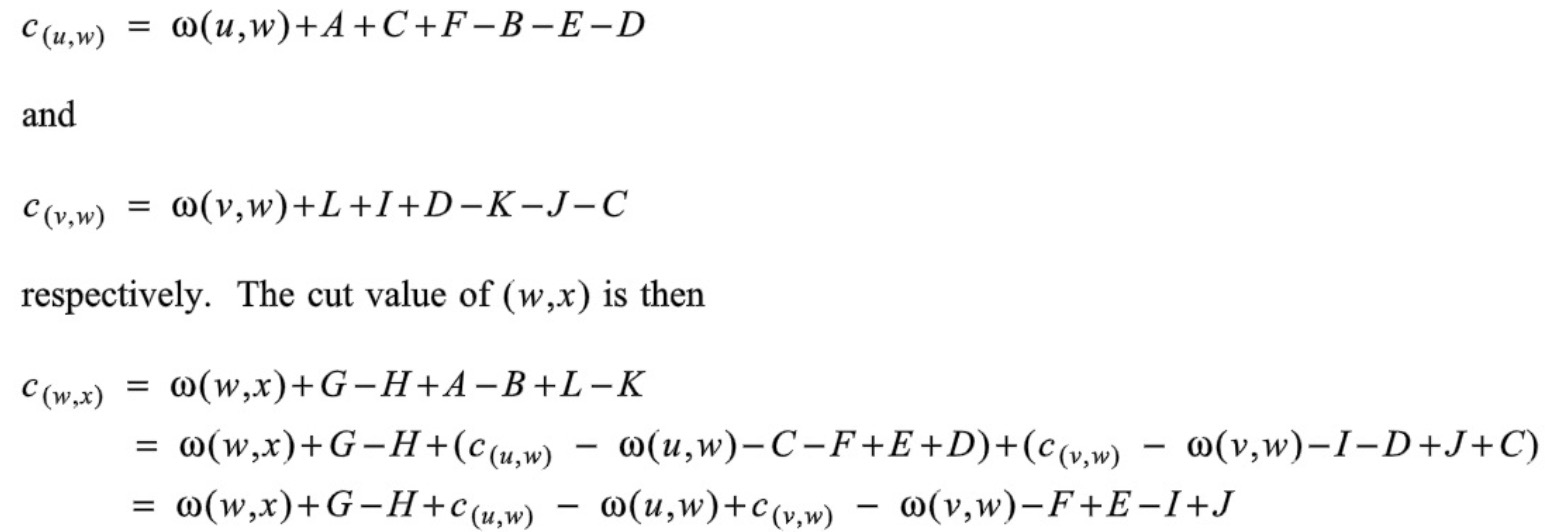
    image.png
    image.png
    从数学公式中，可以看到边的切割值可以通过其相关联边的切割值计算出来。
    对应到场景中，即叶子节点边的切割值直接算出、非叶子节点相关的边的切割值计算公式如下:
    切割值 = 边的weight + 节点其他边切割值之和 + 节点的出边weight - 节点的入边weight。
    整个算法复杂度从原先的深入解读Dagre布局算法 - 图19降到了深入解读Dagre布局算法 - 图20。
    2）将树划分为头部和尾部的优化。
    默认需要遍历所有节点，复杂度深入解读Dagre布局算法 - 图21。
    定义深入解读Dagre布局算法 - 图22和深入解读Dagre布局算法 - 图23，对树做后序遍历，节点在序列中的位置作为深入解读Dagre布局算法 - 图24。计算叶子节点的low = lim，非叶子节点的low等于其子节点low的最小值。
    则在划分区域时，在尾部区域的节点满足以下条件： 源节点的low <= 节点的lim <= 源节点的lim。

五、同层内节点排序

核心思想

返回结果：图中每一个节点都有一个order属性，表示其在同层内的次序
算法步骤：

  1. 针对每一个层级，分别生成两个图，downlayer和uplayer。（见单层级图构建）
  2. 给图中所有节点一个初始的order。
  3. 返回一个层级矩阵，每一个层级对应一个数组，每一层按照节点的顺序进行排序。
  4. 按照节点在所在层级数组中的位置，赋予其初始order。
  5. 遍历downlayer和uplayer，计算每一层级中节点的barycenter和weight（见barycenter的计算）
  6. 根据barycenter的值，调整节点顺序。（见Resolve Conflict）
  7. 根据调整后的结果，重新计算出层级矩阵。
  8. 根据层级矩阵，算出交叉边的个数。
  9. 与上一次计算出的交叉边数作比较，交叉少的排序方案。
  10. 5-8迭代执行4次。（为什么是4次？）
  11. 根据最终得到的order结果，修改图中节点的order属性。

单层级图构建

核心思想：构建一个图，图中包含某层级内所有的节点，以及指向这些节点的边（或从这些节点的边指出）。层级内没有父节点的节点会被当做返回图的根节点，这样更便于移动节点的层次位置。
前置条件：

  1. DAG
  2. 实体节点都有rank属性
  3. 子图节点有minrank和maxrank属性
  4. 边有weight属性

返回结果：

  1. 输出的图中所有的节点都有可移动的层级
  2. 可移动层的根节点，是根据graph的root节点指向的子节点决定的。
  3. 指向可移动节点的不可移动节点（与relationship有关），也包含在图中（无层次结构）
  4. 指向可移动节点的边（与relationship有关），也包含在图中

  5. 如果有相同的边，合并权重成一条边。

    算法步骤

  6. 找到图的根节点，作为返回图的根节点。

  7. 筛选中指定层级内的子图和节点，放到图中。如果不存在parent，就设置根节点为该节点的parent。
  8. 获取节点的入边（与relationship有关），放入到图中。
  9. 如果是子图，将子图的左右边框的同层虚节点也加入到图中。

    示例

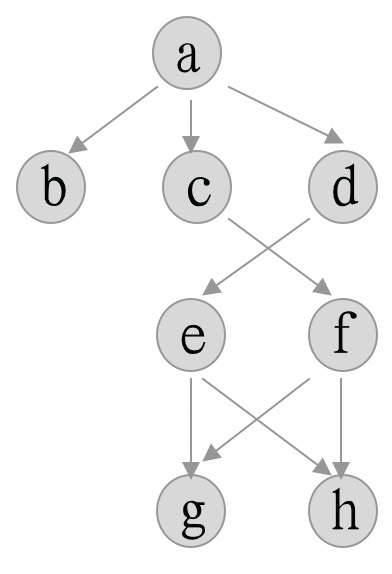
    image.png
    结果：
    downLayerGraph
rank 节点 边
0 a
1 b,c,d a->b, a->c, a->d
2 e,f c->f, d->e
3 g,h e->h, e->g, f->h

upLayerGraph

rank 节点 边
0 a a->b, a->c, a->d
1 b,c,d c->f, d->e
2 e,f c->f, d->e
3 g,h

BaryCenter计算过程

核心思想

计算每个节点的重心值。
简单情况：不考虑边的权重，rank层的节点v1，v2，v1的上游节点u1和v2的上游节点u2位于rank-1层。如果u1的order大于u2的order，那么必须满足v1的order大于v2的order。否则将出现交叉，如下图: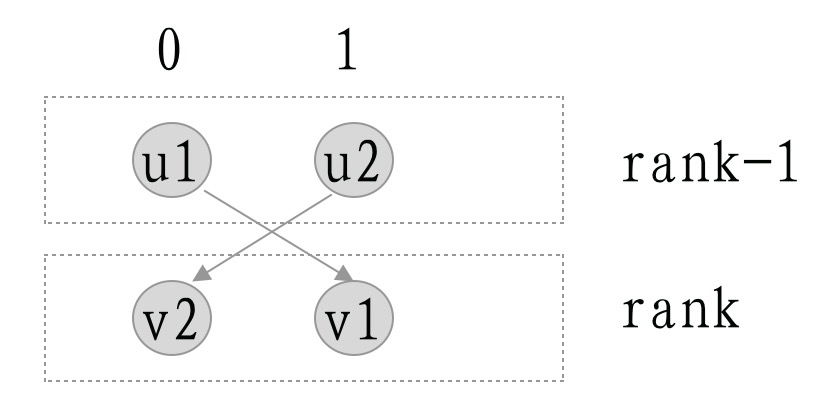
image.png
复杂情况：考虑边的权重，以及节点可能存在多个上游节点。节点上增加属性weight和barycenter。
深入解读Dagre布局算法 - 图27
深入解读Dagre布局算法 - 图28
深入解读Dagre布局算法 - 图29
其中深入解读Dagre布局算法 - 图30表示v节点的order。深入解读Dagre布局算法 - 图31表示边e的weight。
则针对上面例子downLayerGraph[2]，得出如下结果：

节点 weight sum barycenter
e 1 2 2
f 1 1 1

Resolve Conflict

参考论文

A Fast and Simple Hueristic for Constrained Two-Level Crossing Reduction

核心思想

根据上一步计算出来的节点中心值，解决图和节点重心不一致的地方。如果节点的重心值违反了图的约束条件，就合并冲突的节点，使其符合约束条件。
前置条件：输入的数组中，每一个元素都包含{v， barycenter，weight} 或者{v}
返回结果：新的数组，元素 {vs, i, barycenter, weight} 。vs是一个节点列表，里面可能只有一个节点，也有可能是多个节点，这多个节点是需要合并的节点顺序。属性“ i”是“ vs”中任何元素的最低原始索引。
image.png
统一层级中两个节点，如果存在深入解读Dagre布局算法 - 图33，则必须存在深入解读Dagre布局算法 - 图34。否则将肯定存在交叉，这种情况下对换v1和v2即可。

六、布局

节点Y轴

y轴坐标就根据层级来分配，每一层级都是基于上一层级的Y 加上 本层级maxHeight的一半。x,y的坐标是中心点。rankSep是配置项，由使用者配置层级之间的间隔。

  1. function positionY(g) {
  2.   var layering = util.buildLayerMatrix(g);
  3.   var rankSep = g.graph().ranksep;
  4.   var prevY = 0;
  5.   _.forEach(layering, function(layer) {
  6.     var maxHeight = _.max(_.map(layer, function(v) { return g.node(v).height; }));
  7.     _.forEach(layer, function(v) {
  8.       g.node(v).y = prevY + maxHeight / 2;
  9.     });
  10.     prevY += maxHeight + rankSep;
  11.   });
  12. }

节点X轴

参考论文

《Fast and Simple Horizontal Coordinate Assignment》
术语：

  1. 深入解读Dagre布局算法 - 图35表示层级，深入解读Dagre布局算法 - 图36表示节点深入解读Dagre布局算法 - 图37所在的层级。如果有一条边从深入解读Dagre布局算法 - 图38，则深入解读Dagre布局算法 - 图39
  2. 如果边深入解读Dagre布局算法 - 图40存在深入解读Dagre布局算法 - 图41,那么就称这条边为短边，否则，称其为长边。
  3. 定义深入解读Dagre布局算法 - 图42,即节点深入解读Dagre布局算法 - 图43的上游节点；定义深入解读Dagre布局算法 - 图44,即节点深入解读Dagre布局算法 - 图45的下游节点；
  4. 定义深入解读Dagre布局算法 - 图46,即节点深入解读Dagre布局算法 - 图47的入度；定义深入解读Dagre布局算法 - 图48,即节点深入解读Dagre布局算法 - 图49的出度。
  5. 定义图的表达式深入解读Dagre布局算法 - 图50。表示图中的节点由实体节点深入解读Dagre布局算法 - 图51和虚拟节点深入解读Dagre布局算法 - 图52组成，深入解读Dagre布局算法 - 图53表示所有的边，深入解读Dagre布局算法 - 图54表示层级。
  6. 定义图的大小深入解读Dagre布局算法 - 图55
  7. 同层级内节点的顺序关系用<表示，例如深入解读Dagre布局算法 - 图56, 存在关系深入解读Dagre布局算法 - 图57.
  8. 节点在同层内的位置定义为深入解读Dagre布局算法 - 图58
  9. 定义交叉边。
  10. 内部线段：两个虚节点之间的连线

问题定义：
水平坐标分配问题：对于一个给定的分层图，深入解读Dagre布局算法 - 图59，找到深入解读Dagre布局算法 - 图60, 深入解读Dagre布局算法 - 图61，满足深入解读Dagre布局算法 - 图62。其中深入解读Dagre布局算法 - 图63表示最小分割约束。

一个可读性较高的图应该满足：

  1. 边尽量的短
  2. 上下层的节点位置要平衡，长边尽量不要出现拐点。

核心思想

该算法包括三个基本步骤。 前两个步骤执行了四次。

  1. 垂直对齐。尝试将每个顶点与其中上邻或中下邻对齐，然后以最左或最右的方式解决对齐冲突（类型0）。 因此，对于具有最左和最右冲突解决方案的向上和向下对齐的每种组合，我们都获得一个垂直对齐。
  2. 水平压缩。将对齐的顶点约束为获得相同的水平坐标，并且将所有顶点放置在对齐的首选水平方向上，使其尽可能靠近下一个顶点。
  3. 将由此获得的四个分配，即左上、右上、左下、右下四个组合起来以平衡其坐标偏差。

下面以左上这个方面的对齐为示例，说明算法。 其他三种情况是类似的。
1）垂直对齐
在垂直对齐的部分，需要尽可能的将每个层级的顶点与上一个层级相连的顶点对齐。
如果两个对齐方式的对应边线段相交或共享一个顶点，则称这两种对齐方式是冲突的。 我们根据包含的内部线段的数量来对冲突进行分类。
类型2：两个内部线段发生交叉，并且两端线段中都不垂直。
类型1：非内部线段和内部线段有交叉。
类型0：两个非内部线段交叉，或者共用一个节点的非内部线段

三种类型的解决方法~~
类型1：非内部线段和内部线段有交叉。 其次，因为垂直的内部线段是可取的，所以它们被解析为有利于内部线段。我们在Alg1给定的预处理步骤中标记类型1冲突。该算法从左到右遍历各层级（索引l），同时记录两个最接近的内部线段的上邻深入解读Dagre布局算法 - 图64和深入解读Dagre布局算法 - 图65。 算法复杂度为深入解读Dagre布局算法 - 图66。同时算法中还标记了类型1冲突的非内部线段，便于在确定对齐方式时忽略它们。
可以很容易地修改这个预处理算法，用来标记类型2冲突，或通过交换交叉内部线段的较低顶点来即时消除它们。
image.png
类型0：两个非内部线段交叉，或者共用一个节点的非内部线段。我们定义如果节点v在v’的左边，u在u’的左边，那么线段（u，v）一定在线段（u’,v’）的左边。类型0冲突以最左端的方式贪婪地解决，即在每一层，从左到右遍历顶点，考虑其中上邻节点（如果有两个，就按照左右顺序）。 如果没有冲突的对齐，则该对将对齐。 所产生的偏差是由以下事实引起的：将对称偏差应用于其他三个分配之一。
通过下面的算法，我们就得到了一个左侧向上对齐方式。垂直对齐最多的节点，我们称之为block，定义最顶部的节点为这个block的root节点。请注意，block用循环链接列表表示，其中每个顶点都引用了其下对齐的邻居，而最低的顶点又引用了最上层的邻居。 此外，每个顶点还具有对其root节点的附加引用。 这些数据结构足以满足下一节中描述的实际放置。
image.png
【水平压缩】
分配水平坐标。一个block共享root节点的水平坐标。如左图对应的block划分为右图所示。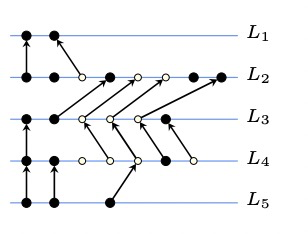
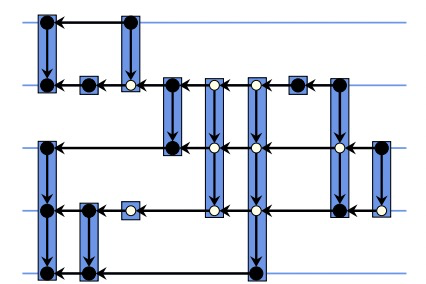
image.pngimage.png
观察图，每个block的root节点就是这个无环图的sink，通过在层间的左上角，同时同一层级最多有一个这样的节点
我们将框图划分为多个类。块所属的类由其最高根节点决定。在每个类中，我们应用最长路径分层算法，即，block相对于sink的相对坐标，递归的计算为相同类别中的上一个block的最大坐标加上最小间隔。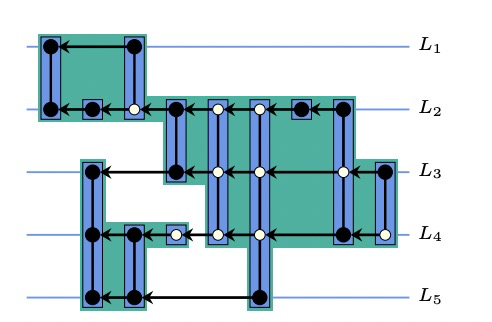
image.png
image.png
然后，对于每个类，从上到下，我们通过将类与先前放置的类之间的距离最小化，来计算其成员的绝对坐标。
整个压缩算法如alg3所示。
第一次迭代使用了最长路径分层算法的递归版本，计算出相对于类接收器的所有根的相对坐标。 然后，计算每个接收器类中的一个顶点，与具有更高接收器的类中其相邻顶点之间的最小距离。 第二次迭代将这些信息从根部分发到所有顶点以获得绝对坐标。
image.png
以上即为迭代四次后，分别得到的左上、左下、右上、右下的四个图。下面根据四个图做平衡
【平衡】
最简单的平衡，横坐标根据左右两个图中节点的横坐标取平均值。

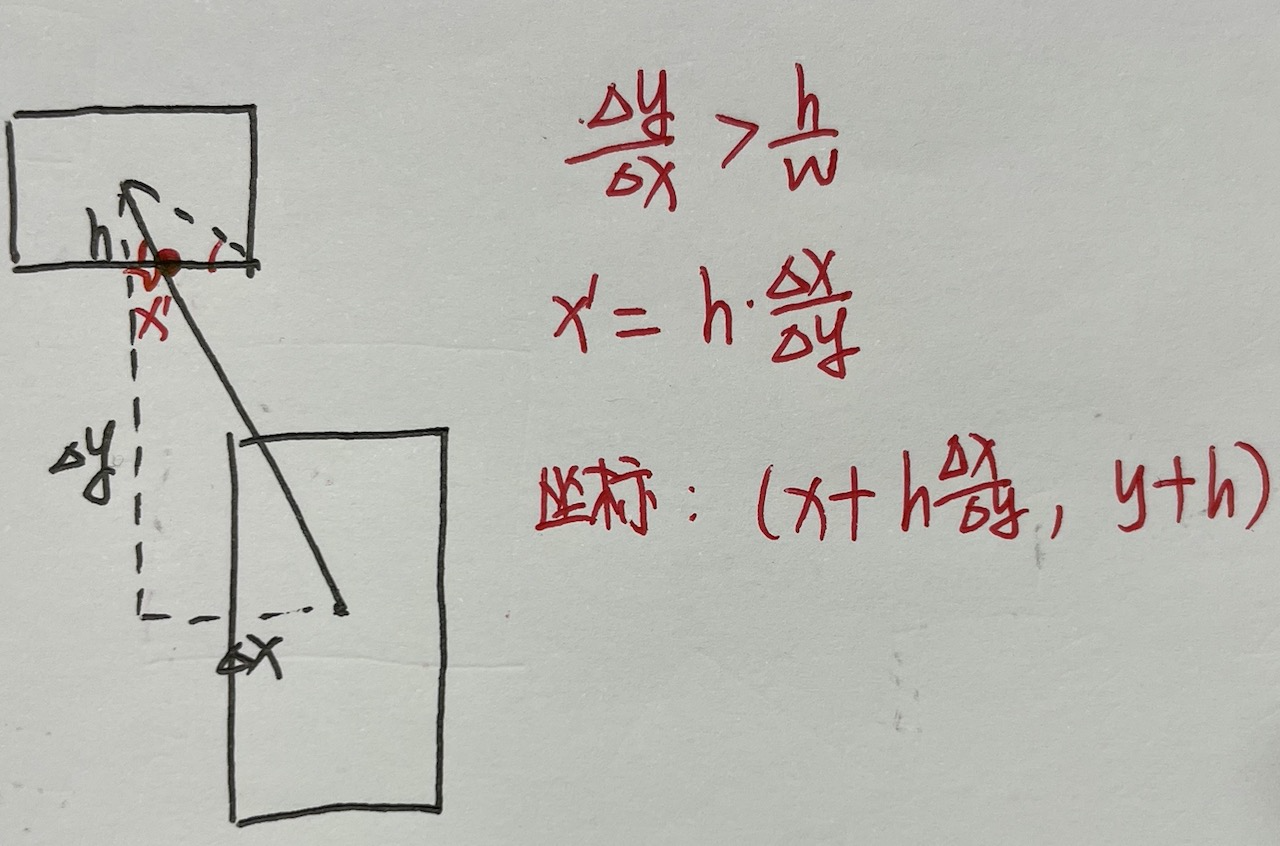
边的路径计算

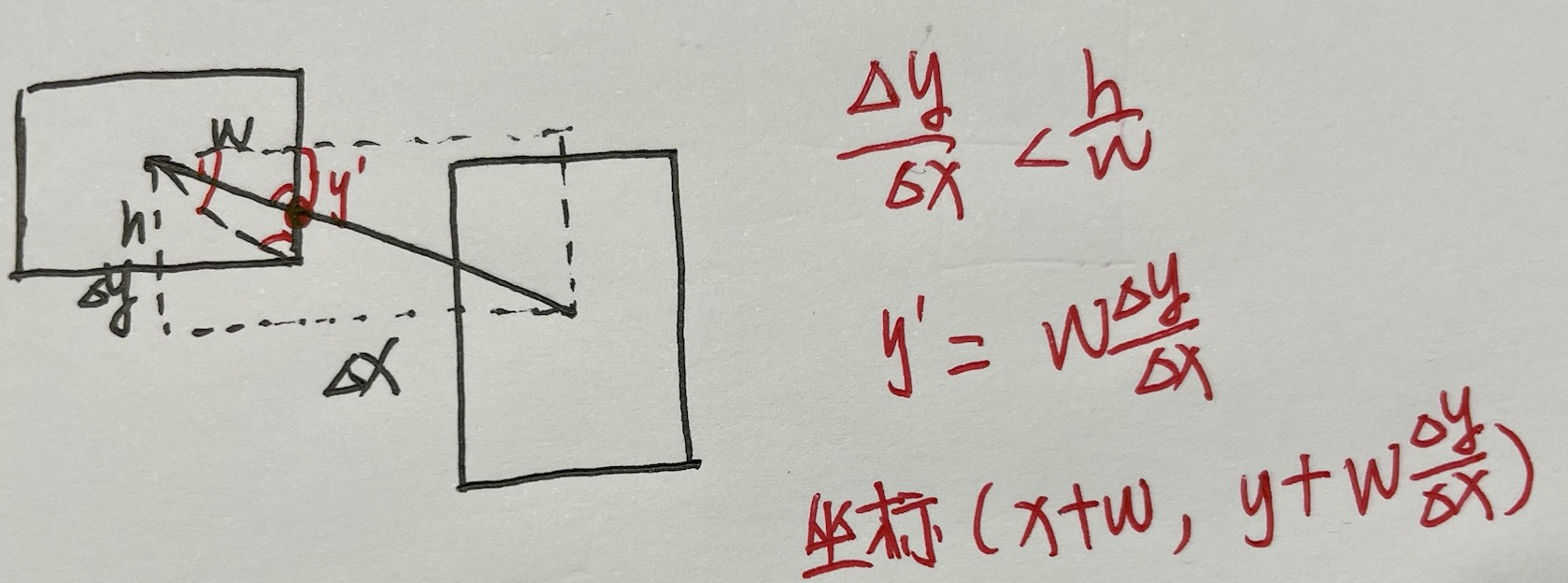
计算出边的point坐标，是的边不传过box，同时边指向box的中心。
即如何算出a和b的坐标。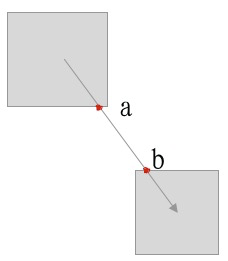
image.png
image.png
image.png

七、嵌套子图的处理

参考论文

Layout of Compound Directed Graphs

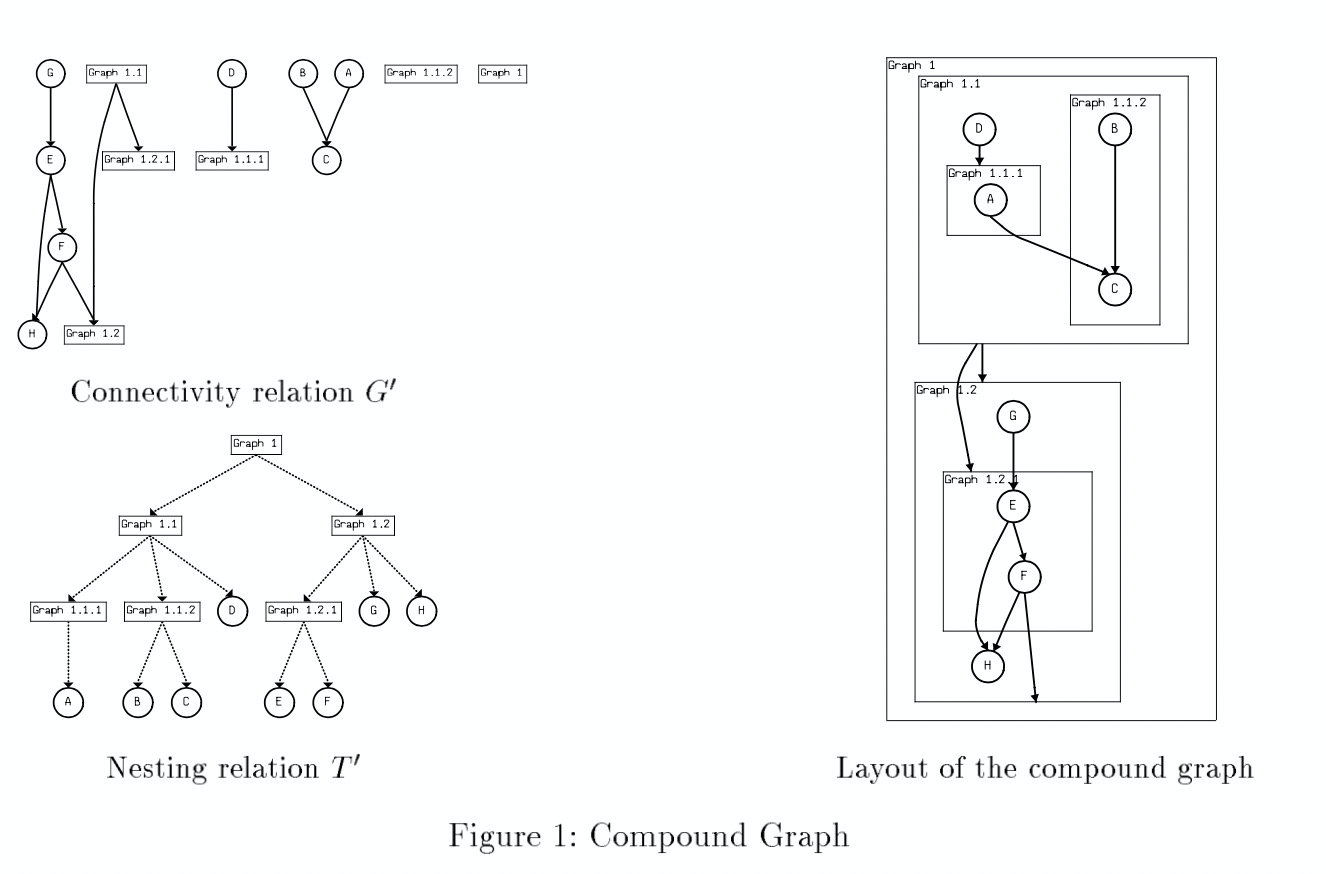
核心思想

基于分层布局，把一个子图当做虚拟节点，然后全局划分所有节点到不同的层级，再调整统一层级内节点的顺序，避免产生交叉线。论文中定义，所有的嵌套图都可以用一个连通关系图深入解读Dagre布局算法 - 图77和一个嵌套关系图深入解读Dagre布局算法 - 图78表示。如下图
image.png

层级划分

层级分配规则：
a. 所有的节点都需要划分到不同的层级，同一层级的节点，y轴坐标一致。
b. 节点之间，节点与线之间不能有重叠交叉
c. 线之间可能有拐点和交叉，要尽量避免
d. 边应该尽可能保持方向一致，比如从上到下。
e. 矩形边框内应该包含所有在子图内的节点。
f. 两个子图之间的矩形边框，不能有重叠
g. 线可能会与子图的边框有交叉，应该尽量避免。
h. 减少跨级的边，如果有，就通过产生虚拟节点的方式来消除跨级边**
划分定义：
a. 对于每一个子图，都有两个虚拟节点，虚拟节点深入解读Dagre布局算法 - 图80 表示图顶部，虚拟节点深入解读Dagre布局算法 - 图81表示图底部。
b. 同时虚拟节点和真实节点不能处于同一层级。
c. 两个不同层级的节点之间，至少有2k个层级，其中k是嵌套关系树的深度。如下图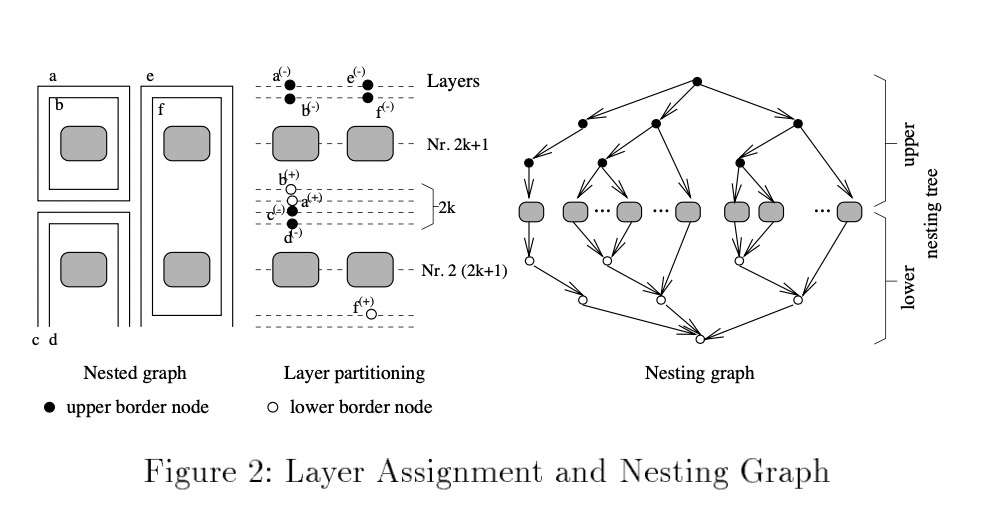
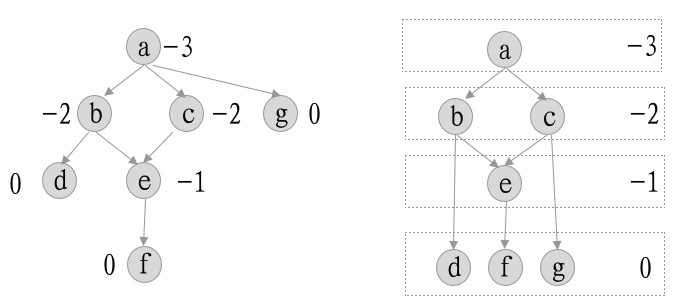
image.png
可以看出最终得到嵌套图中upper和lower是对称的。所以问题可以转换为求所有实体节点v和虚节点u-的层级。

公式一： 节点来说，其层级就是它的所有父节点中层级最大值+1，即
深入解读Dagre布局算法 - 图83
我们可以根据上面的计算，得出所有节点的层级如右图。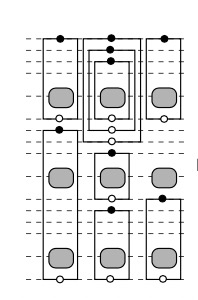
image.png
但是看得出这个图的问题，就是子图内的布局很空旷，因为子图的虚拟节点深入解读Dagre布局算法 - 图85 离内部的实体节点很远。所以需要进一步的优化
公式二：虚拟节点的顶部应该离内部的实例节点越近越好，即
深入解读Dagre布局算法 - 图86
优化后的层级图如下图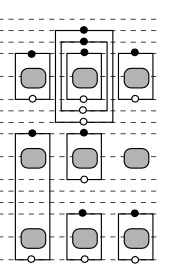
image.png

生成虚拟节点

找到子图中合适的点，作为连通线的端点。对于子图深入解读Dagre布局算法 - 图88和深入解读Dagre布局算法 - 图89来说，（深入解读Dagre布局算法 - 图90）,（深入解读Dagre布局算法 - 图91）,（深入解读Dagre布局算法 - 图92）都是一样的，代表同一条线。
在这个过程中，同样要避免产生环，如果过程中产生了反向的边（如从下到上的边），就把边做标记并反转过来，布局结束后再把边恢复。
把跨多个层级的长边，通过生成中间虚拟节点的方式，将其分割为多条边。从而使得图中所有的边的长度均为1。
在一个嵌套图中，所有的节点必须都是在一个图中，所以生成一个虚拟根节点。
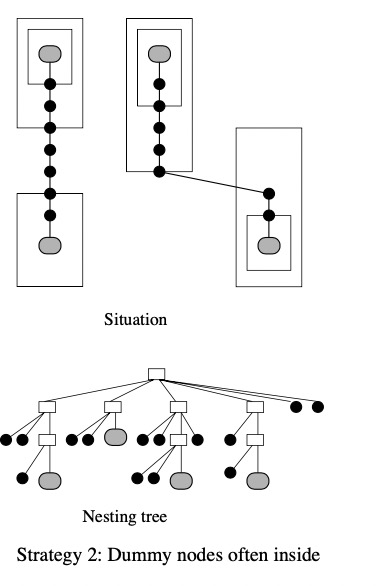
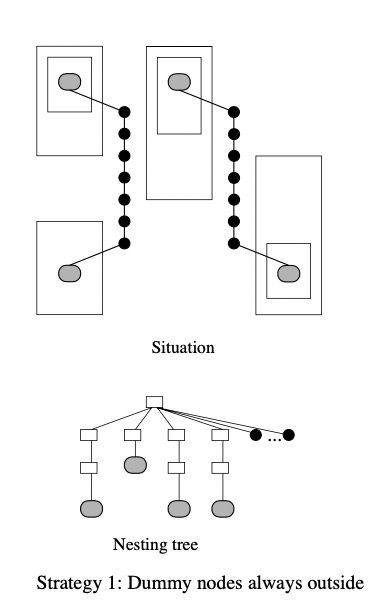
虚拟节点生成过程有以下两个策略：

  1. 将边深入解读Dagre布局算法 - 图93尽可能的布局在子图边框外。如果节点深入解读Dagre布局算法 - 图94不在同一个子图内，就穿过各自的子图，将它们的边全部都布局到子图外部。在嵌套树中，我们找到这两个节点的第一个父节点，然后把生成的虚节点放到树的边缘。如下图

image.png

  1. 将边深入解读Dagre布局算法 - 图96尽可能的布局在子图边框内。如果节点深入解读Dagre布局算法 - 图97不在同一个子图内，通过调整它们所在子图的区域，将边尽量的放到子图内。对于嵌套树来说，需要找到对应的子图，然后把图内的虚拟节点添加到子图中。如下图所示：

image.png