引言 —— 你知道能源是如何流转的吗？人类是如何掌控能源的来源、中间环节、最终去向的？如何生成一张清晰表达能源流转的图？数以百计的图布局算法，究竟哪个适合展示能源流转？本文将分析各种布局，最终以最佳方式展现能源的流转。如果你想直接查看能量图最终结果及其分析，请直接滑至本文结尾处。

本文中的图可视化由 G6 提供支持。 G6 —— 专业的图可视化引擎。让关系数据变得简单透明，让用户获得 Insight。 G6 官网：antv.alipay.com/zh-cn/g…。欢迎关注。 GitHub：github.com/antvis/g6。欢迎 Star。

前言

从古至今，能源都是人类生存的基础。古时候，人们利用如动物粪便、草木柴薪等生物能源为之提供光和热。现代社会，能源的来源更丰富了：石油、核能、风力……人类更加离不开能源，它也是社会发展和经济发展的推动力。能源的来源和节约是人们关注的问题。那么，当今人类又是如何掌控和利用能源的呢，又有多少能源是被人类白白浪费的？为了分析上述能源数据，本文将与您一起探索如何制作能量图可视化。如果您（不想看啰里八嗦的布局选择）想直接查看能量图的最终可视化及其分析，请直接滑至本文结尾处。

在上一篇 Graph Visualization · 知多少：《Hello World 图可视化》 一文中，我们已经知道了图的可视化方法主要有三种：弧线图、邻接矩阵、点线图。其中，点线图（如下图，点线图是由节点和线/边构成的图，节点是实体/对象，边是对象间关系）是最为流行的一种。本文将围绕点线图，设计一个适合展示能源流转的图可视化。

能源数据 -> 图

本文使用的能源数据是各个能源环节之间的能源输入、输出关系。例如从太阳能到电能的能量流转、电能到家用电的能量流转等。

图特别适用于展现实体/对象之间的关系。而能量数据的重要信息也在于各环节之间的能量流转关系。每个能源流转/转换是存在于两个相关环节之间的。因此每个环节可以被视作点线图中的节点，能源流转则是连接两个环节节点的边。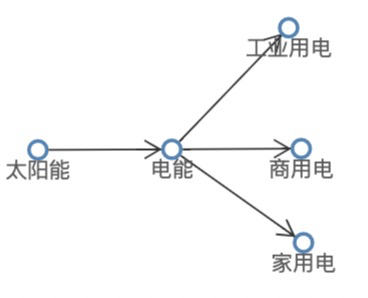

能源图 VS 布局

什么是布局？
布局是用于点线图中的节点位置的放置方式。相对应地，布局算法是用于自动计算节点位置的算法。举个栗子，上图中太阳能节点在左侧，电能节点在中间，其他节点在右侧，这样的安排就算是一种布局。在节点较多、关系复杂的图上，无法手动指定每个节点位置。此时可以借助布局算法，依据关系自动计算节点位置。有了合理的布局，才能可视化出清晰的关系。

为什么要用布局算法？
以能源数据为例，如果要将能源数据呈现成为屏幕中的一张图，就需要为每一个节点指定它在屏幕中的位置。然而能源数据中的对象和关系非常复杂，手动指定位置不现实（不信你手动摆一摆节点试试，能拖出一个合理美观的图算我输），只能依靠强大的布局算法。

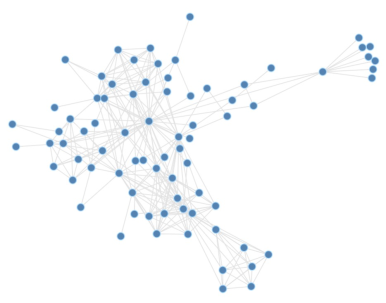
-PD：布局算法这么厉害，那我用一下就完事儿了呗？ -我：NoNo，布局算法有好多好多呢，下图随便列举了几个，你随意感受一下，你知道哪种更好吗？- PD：as#%9jafsk31#!!!…

布局方法千千万，究竟哪种最好？我们认为，布局没有好坏之分，只有适合与否之分。根据不同的数据结构、使用场景、分析需求，选定一个合适的布局是一个图可视化是否成功的关键。下文将分析各类布局中较为常见的算法，最终选取适合能源图的布局。

在图可视化中，根据其数据的结构中是否存在环，可以归类为一般图和树图（Tree Graph）。一般图允许存在环，而树图中不存在环。下面，我们将分析多种树图布局、一般图布局，以选择和适用于能源流转的图可视化布局。

树图布局

离散数学告诉我们，树是一种数据结构。相比于一般图的数据结构，树图不存在环，除根节点外，每个节点只有一个先继（父）节点。树更简单、更易理解。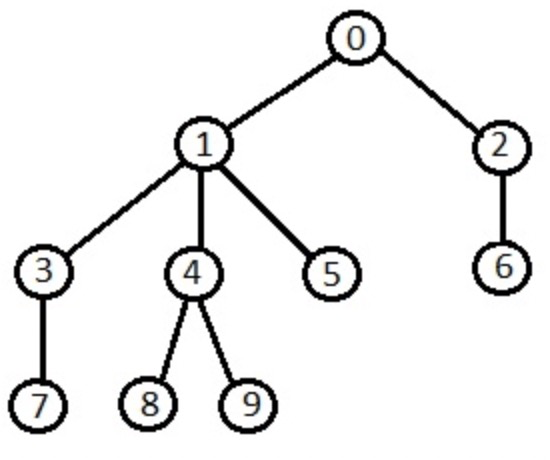

树图常被应用在家谱、生物进化等表达中，从根到叶子的一条路径代表了从源头到最终形态的过程（我是 7 号，我爸爸的爸爸的爸爸是谁？）。

对于树图，研究者们提出了不少树图的布局。这些布局各有优劣，图 3（左）最为直观，但它对屏幕空间的利用率不高。图 3（中）将树根据节点的深度布局成辐射状，以更好地利用空间。图 3（右）显示的气球布局将子树布局到父节点周围。但后两种方法不如图 3 （左）图清晰，用户常常在探索过程中感到困惑。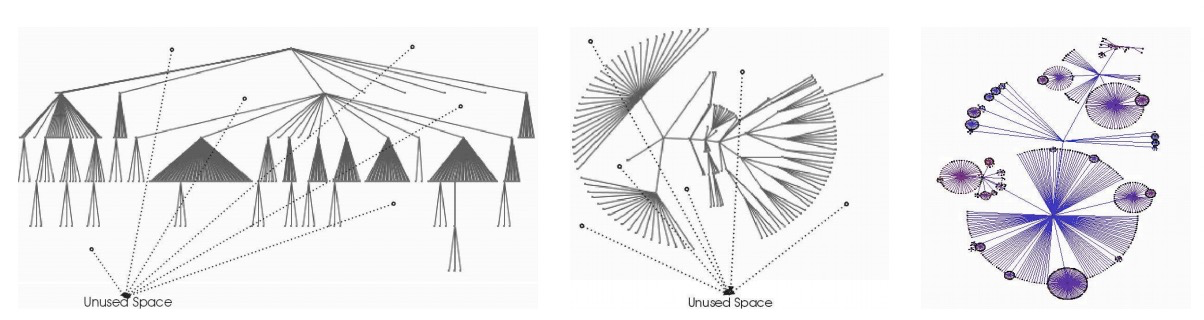

图 3. 点线图布局策略：（左）大规模图的经典层次视图。（中）辐射状视图。（右）气球视图。

对于经典的层次视图，根据层级之间的放置规律，已有一些成熟的算法，图 4 使用 G6 提供的几种树图布局：

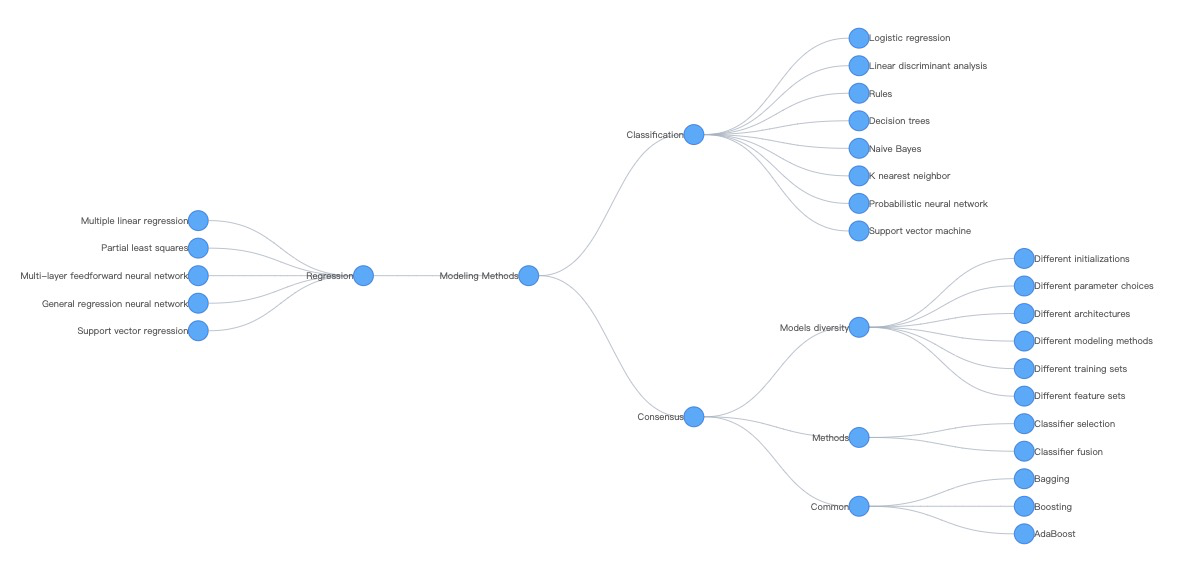
图 4. 使用 G6 绘制的树图：（左）紧凑树布局 CompactBox 将深度相同的节点放置在同一视觉层级上。（中）脑图树布局 Mindmap 可以将分支分离到根节点的左右两侧。（右）辐射树布局。

与树图相似，能源图希望表达从能源的来源到最终去向的路径。但别忽略了其中的环结构：如下图，由于能源的流失也算是一个去向节点，电力的来源可能来自于核能、风能等，电力的去向也可能是工业或流失等，而核能也可能直接流失了。显然，由于数据结构的问题，能源图应该被划分到一般图。上述树图布局都不适用。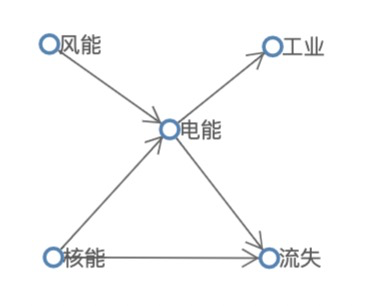

树 + 回溯边（非树边）布局

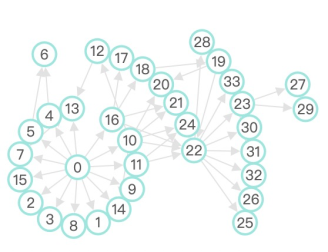
既然能源图数据不是一个树结构，那么，我们是否能借助树图的层次和简明性，降低其复杂性呢？一些图可视化研究者从一般图的抽取一棵生成树进行展示，不展示回溯边（非树边）。例如 图 5 展示了从灰色的原图计算了其最小生成树（红色）：

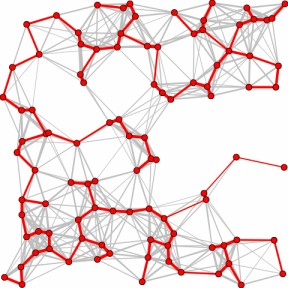
图 5. 原图是灰色及红色所有元素组成的图，所有节点及红色边构成的图是原图的最小生成树（Minimum Spanning Tree）。

但直接展示最小生成树必然丢失一些重要的关系信息（非树边）。因此，一般图还可以被可视化为树 + 非树边。在绘制完生成树后，将剩余的非树边绘制回图上（见图 6（左））。例如经典的树图，辐射状视图，以及 treemap 视图[5, 6]许多可视化系统，例如，都使用了这种方法。

图 6. 树+边布局：（左）经典树布局增加了其他非树边。（中）辐射状视图增加了其他非树边。（右）Treemaps 视图增加了其他非树边。

现在，我们尝试使用树图 + 回溯边的方式布局能源流转图。树图虽然易于观察和探索，但选取的根节点合适与否将会影响整个图的表达，根节点一般是一个能够代表图的起源或开端的节点（爸爸的爸爸的爸爸是不能乱选的！）。图 7 所示的能源图树布局选取的根节点并不是所有能源环节的源头，这是因为能源图中的起源点可能不只一个，核能、石油、风能、潮汐能一类能源的最初形态都是能源流转的起源。也就是说在该图上，选取任何一个节点作为根节点都不合适。另外，图 7（右）将非树边绘制回图上后，产生了一些很长的边，跨越整个图，造成了众多边交叉，这些是不符合图布局的美学原则[12]的。（啊喂，那几条竖直的边，你到底是要连到谁呀。）

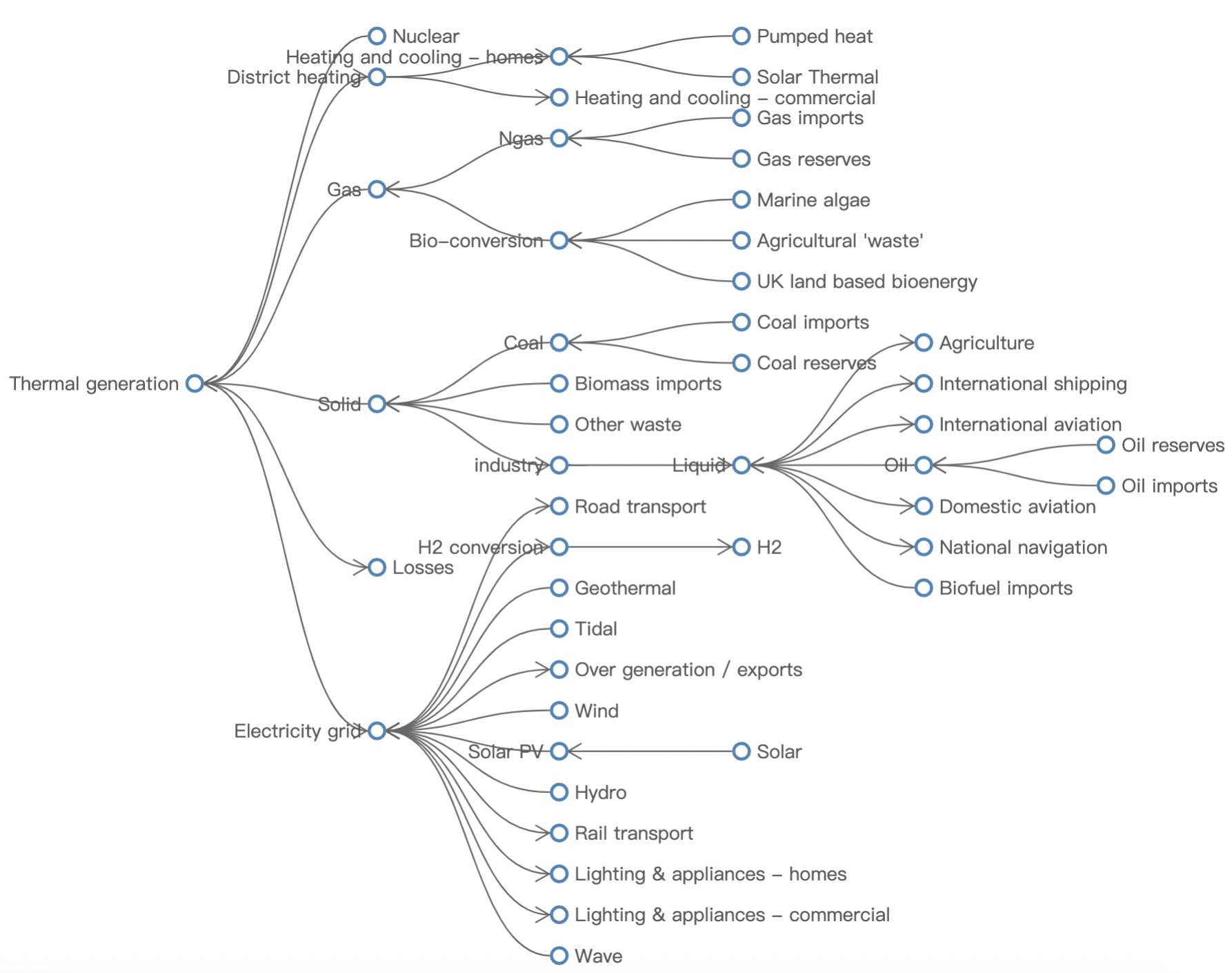
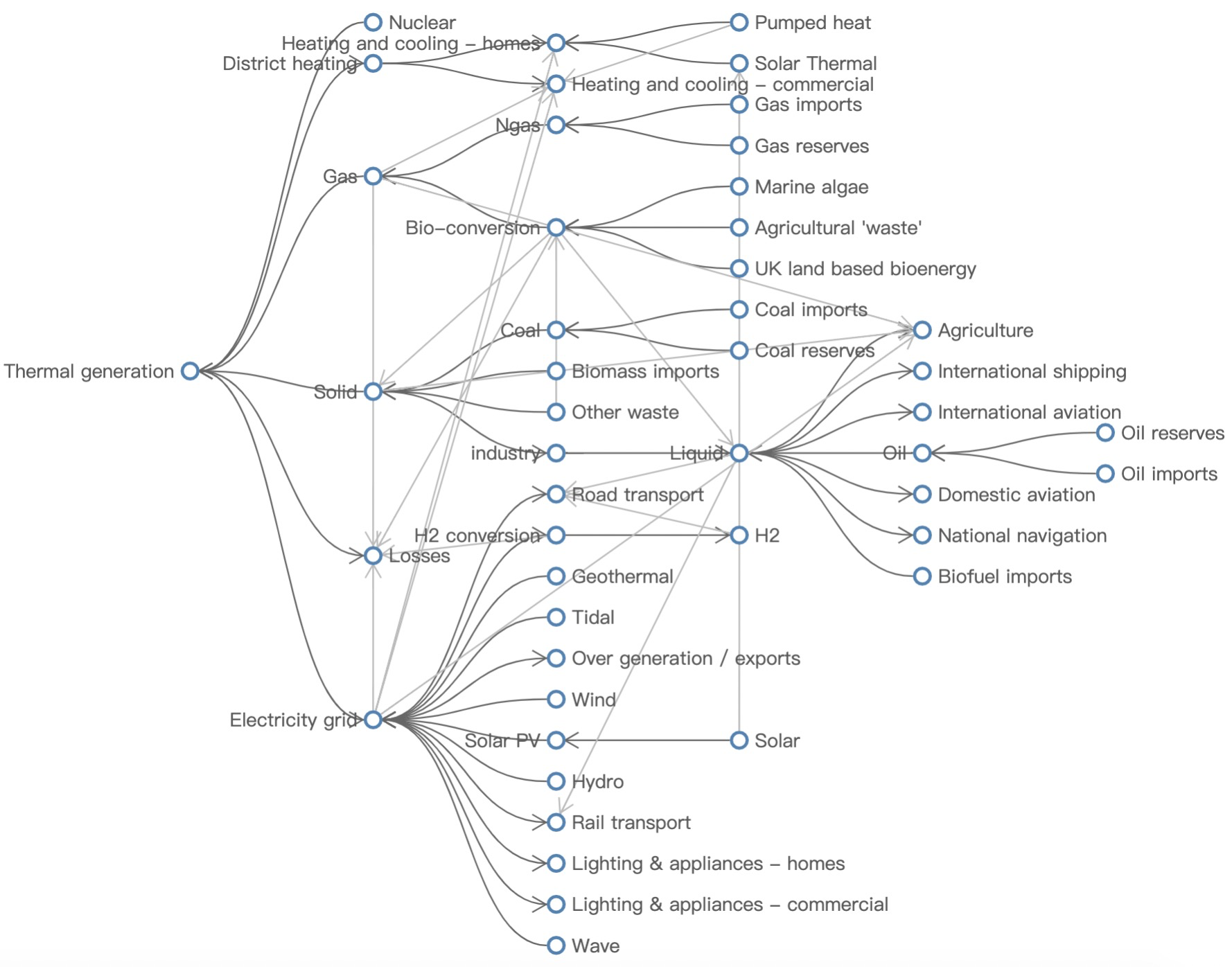
图 7. （左）从能源图抽取的树，使用紧凑树布局。（右）将非树边（浅灰色边）绘制到左图的树布局中。

虽然在这种布局方式在能源图上不适用，但若数据的边是包含层次关系类型的多种类型的边，树+边布局则非常适用。例如，WebMap[8]一文设计了用户网页浏览器浏览历史记录的可视化。如果网页 A 被第一次访问，一个代表该网页的新节点将会被添加在它的先继节点（即代表上一个网页的节点）之后。如果网页 A 曾经被浏览过，当其再次被浏览时，一个穿过树结构的非树边将会被创建以连接节点 A 和它的先继节点。

其他布局方法

既然使用树布局的方法展示非树结构的能源图不合适，下文将尝试其他一般图布局方法。（不要为了一棵树放弃一片森林啊。）

弹簧布局 / 力导向布局

弹簧布局，即被熟知的力导向布局，是另一种流行的一般图布局策略。在弹簧布局中，一般图被建模成具有环和弹簧的物理系统。作为绘制一般图的最早实际算法之一，弹簧布局最早在 1984 年被 Eades 提出后，被许多研究重新定义和改进。

图 7. 力导向布局。

扩展：研究人员还尝试使用弹簧的原理减少节点的重叠11, 19[]。完全解决一个小空间范围内的图中所有节点的重叠问题，已被证明是 NP 难的__。（PD：能不能把这个边交叉、点重叠搞少一点，好丑好乱。我：优化优化可以，全部消除是莫得办法的呀，NP 难的世界难题，你给我搞比科研经费我给你研究一辈子试试。）

图 8 尝试使用力导向布局展示能源图，节点大小映射了该能源环节点的总能量值；边的箭头代表能源流转的方向，粗细代表沿该流转的能量值。可以发现与电力网（Electricity grid）节点相关的边数量最多，但它的总能量值不如 热能生成（Thermal generation）节点，这是个有趣的发现，原来人们对电能的产生和使用渠道比较多，但对热能的需求量更高。同样，从节点大小和相关边数量还可以看出，人类对太阳能（Solar）、氢气能（H2）、风能（Wind）等清洁能源的利用还比较小。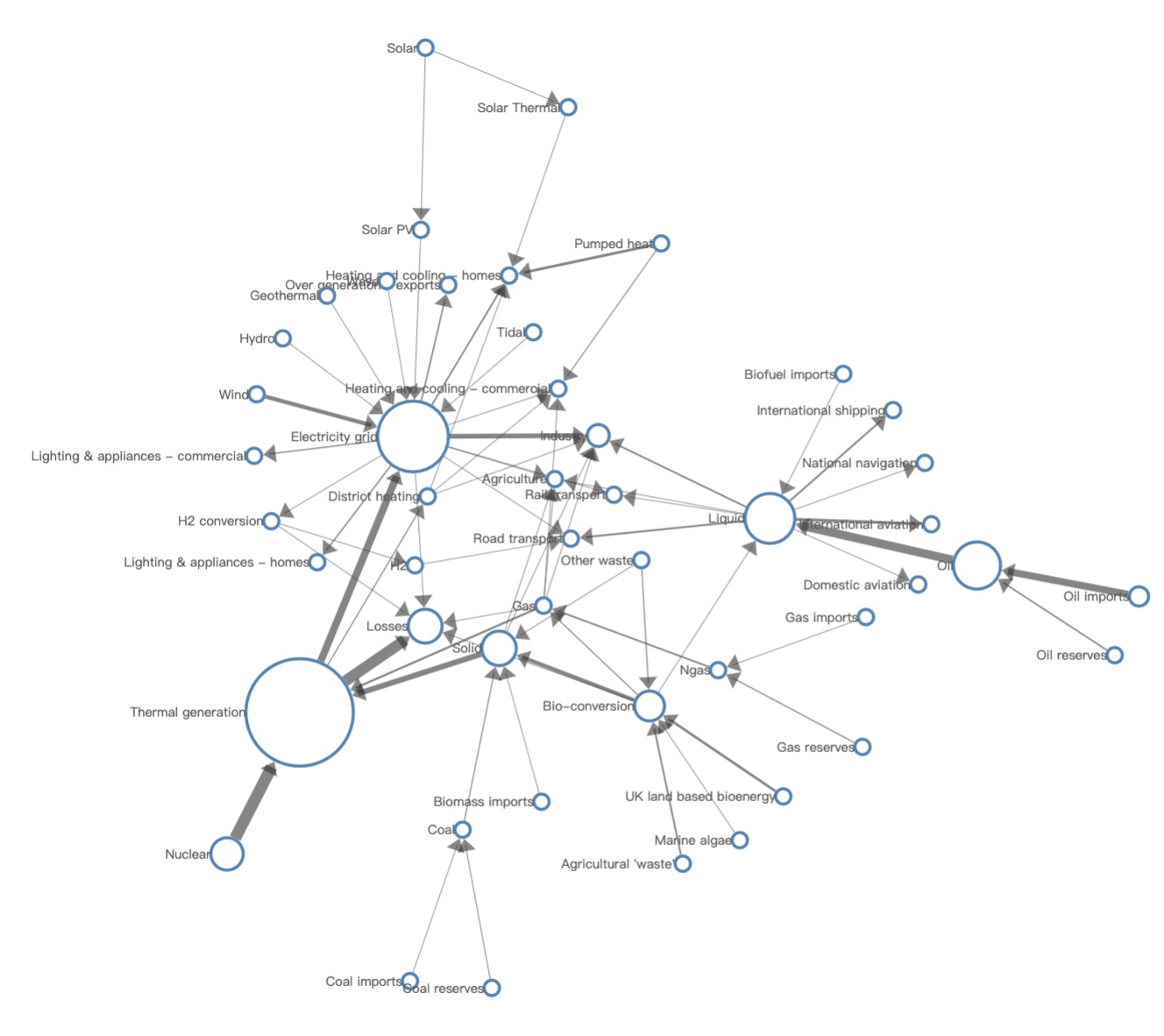

图 8. 使用力导向图布局展示能源图。

虽然力导向图能够带给我们一些有趣的信息，但我们还是难以清晰了解能源从产生到使用的各环节流转情况。力导向图的另外一个弊端在于，它的计算量庞大（需要 甚至 的时间复杂度），一遇到大规模图算法就要宕机了。而且，力导向算法在可预测性方面存在缺陷 —— 相同算法在同样的输入下，每次运行的结果可能完全不同。由于用户的导航探索重度依赖于图的视觉表现，这种不可预测性在某些场景中导致了一些严重的问题。如 图 9 所示，力导向算法在能量图数据上又运行了 3 次，均产生了不同的布局结果，这将导致用户在探索、对比时的心理地图遭到破坏。（PD：喂喂，这几张真的是同一幅图吗？你的代码是不是有问题，改了我的数据！？我：冤枉啊。）

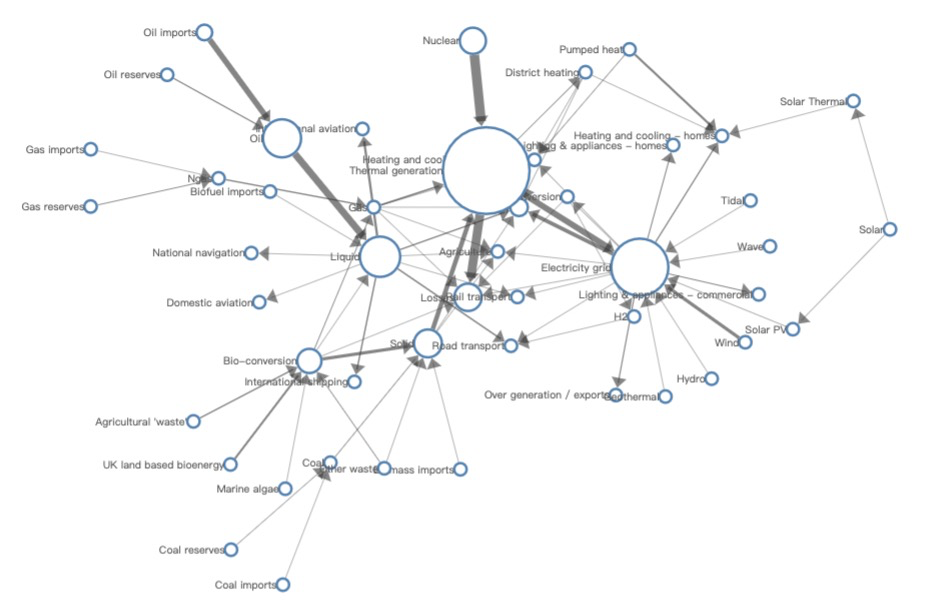
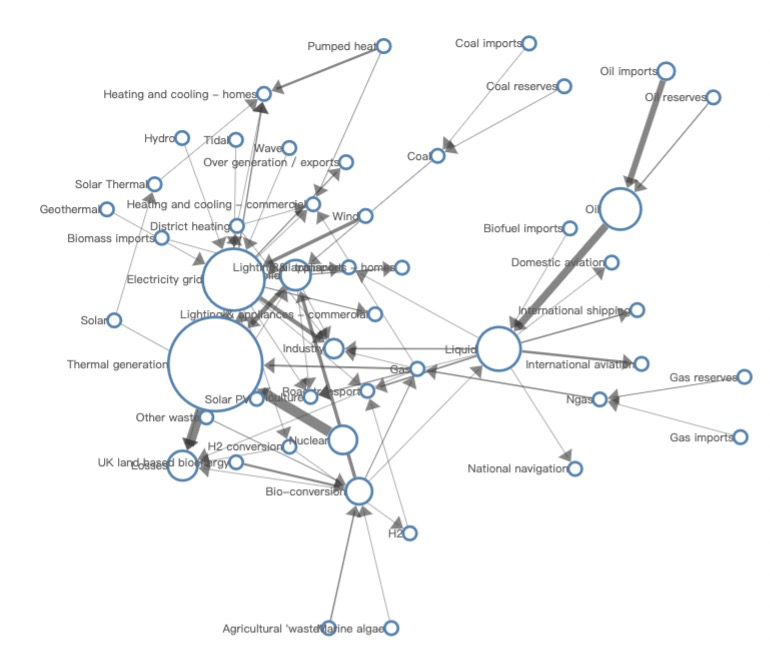
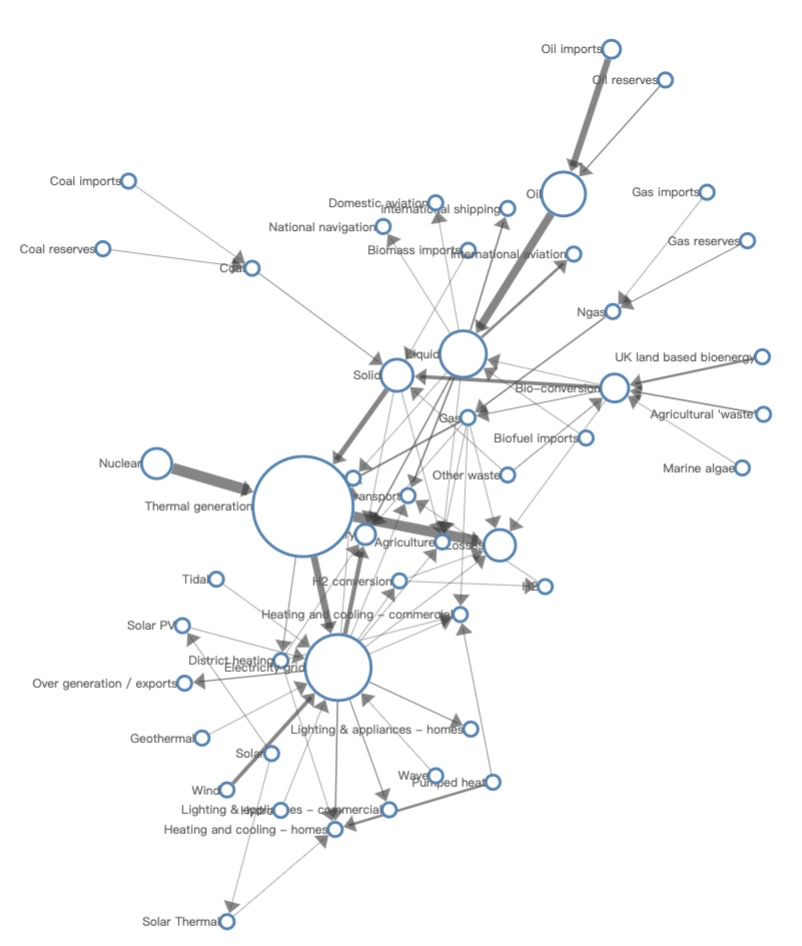
图 9. 使用同样的数据，每次运行经典力导向算法的布局结果都不同。

形状导向的点线布局

为突出某些信息或达到某些视觉需求，一些形状导向的点线布局被提出。例如环状布局（Circular Layout）可用于突出数据结构中的环，但如 图 10（左）将之应用到非环结构的图上时，节点的排列顺序将会影响边的交叉数量；再如图 10（中）的格子布局（Grid Layout）可以让简单图看起来十分规整，但在关系复杂的图上将会出现大量长边和边交叉。显然，这两种布局对于分析能源图没有太大的帮助，只能满足一种“整齐”的视觉需求。（PD：嗯嗯，一家人整整齐齐，真不错。我：这…你能分析出啥？）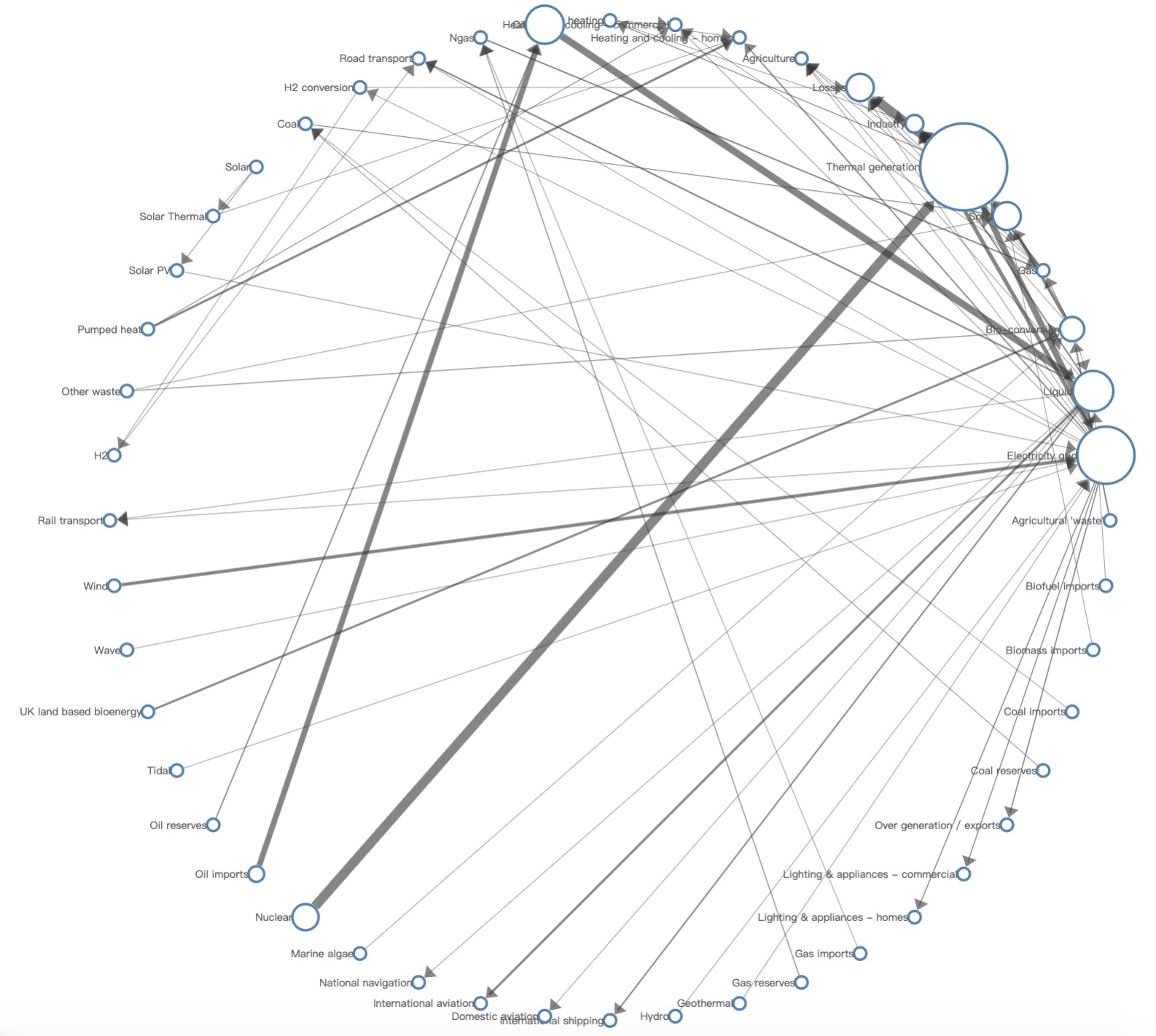

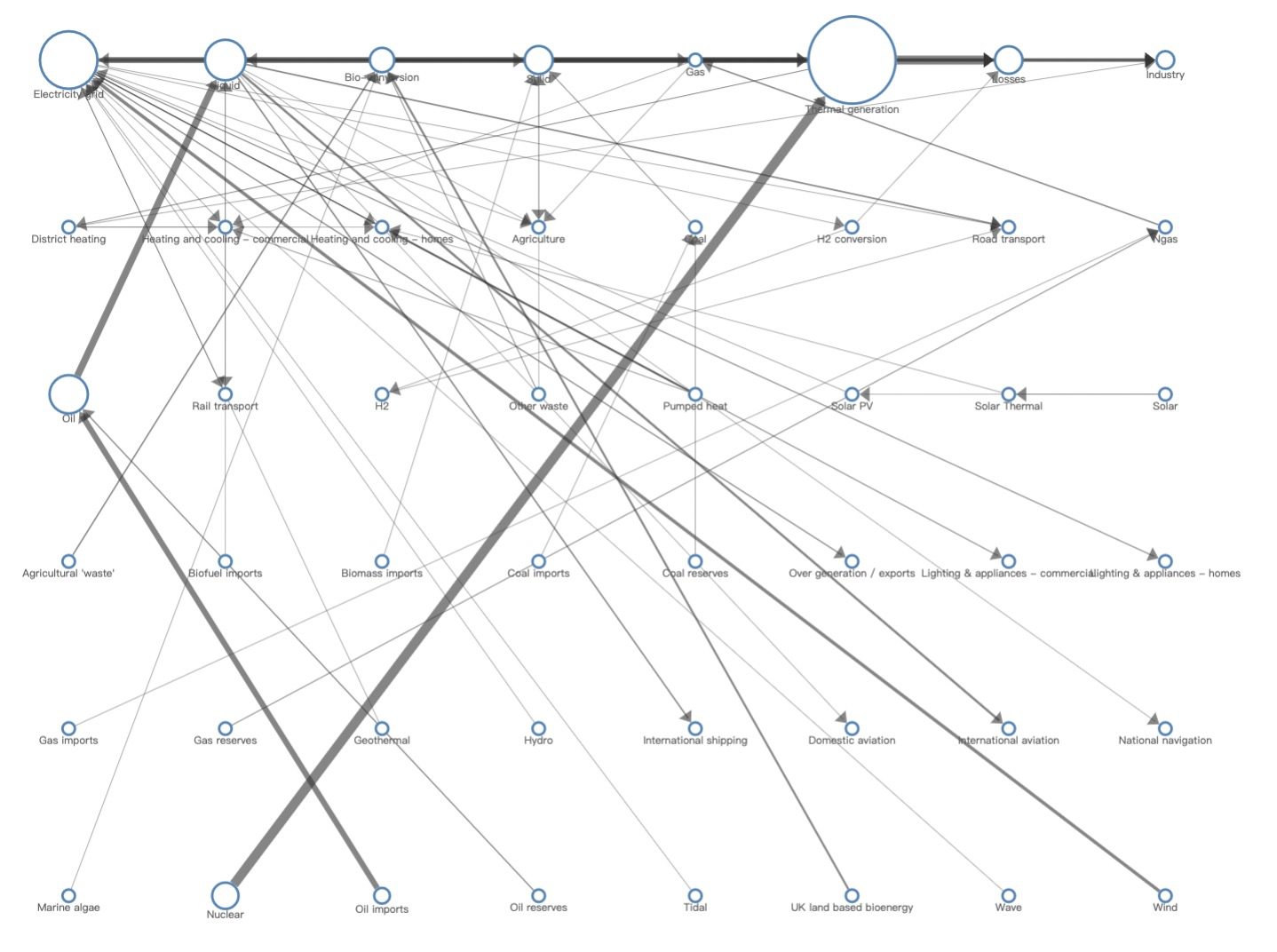
图 10. 使用 G6 制作的形状导向布局：（左）环状布局。（中）格子布局。（右）辐射状布局。

辐射状布局（Radial Layout）是辐射状树布局[1]的扩展，可突出关注点与其他节点的最短路径关系。图 11 使用 G6 展示了能量图的辐射状布局，其关注点是核能（Nuclear）。作为能源起源点之一，根据其输出可以发现核能（Nuclear）的能量全部用于热转换（Thermal generation）。根据关系边的粗细可以发现，热转换后大部分流失了（Losses）（心疼 1 秒钟），还有一部分被转换为电力（Electricity grid）和供暖（Distrct heating），接下去用户可以探索电力网的直接输入与输出环节。辐射状布局适用于探索关注点的一度关系、二度关系、…等，但在能源图上，我们更希望从多个能源起源点出发，关注能源流转。因此，辐射状布局并不完全适用。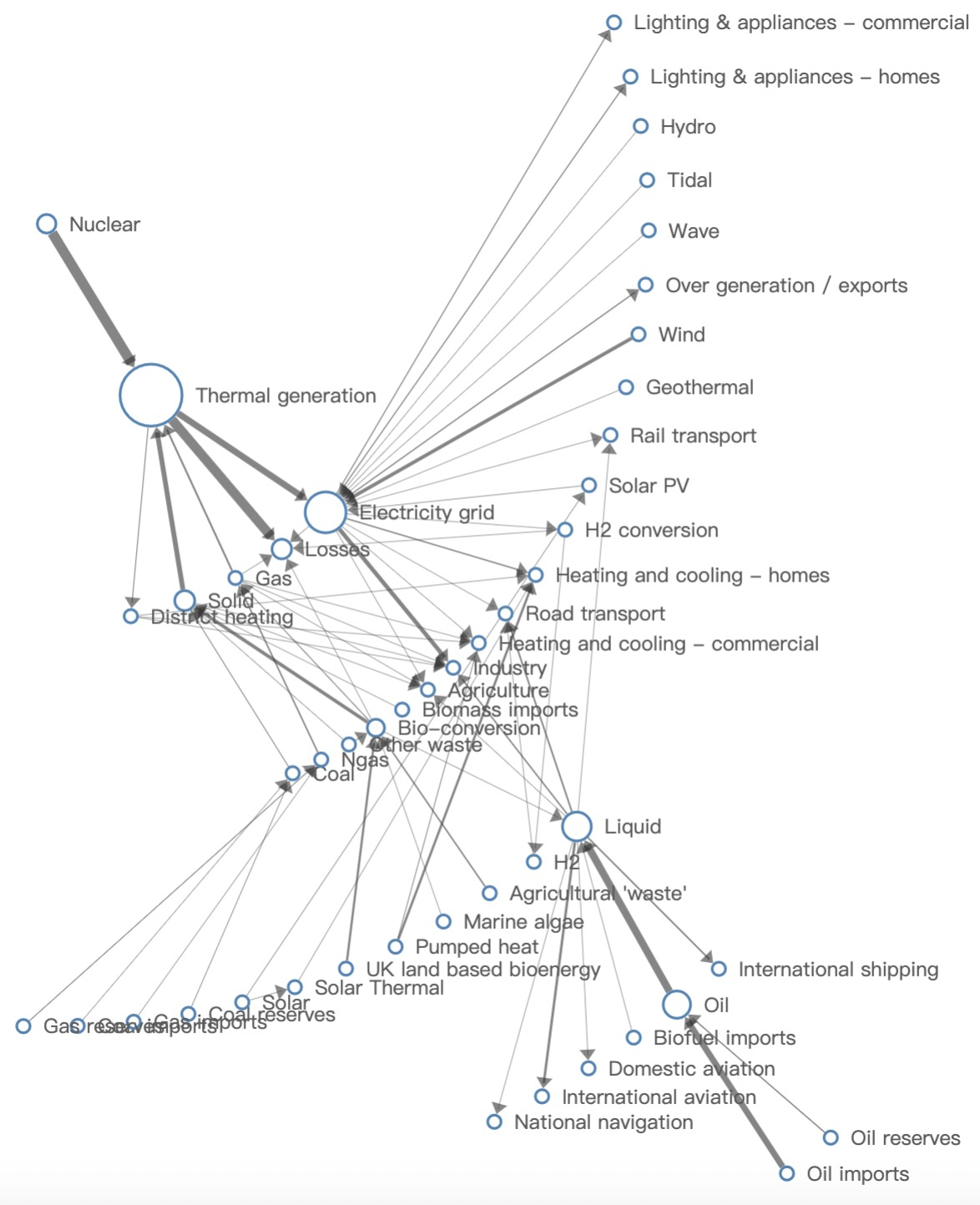

图 11. 使用 G6 展示辐射状布局的能量图。

层次 / 流程图布局

为了展示能量图中各环节的流转，流程图似乎比较适合。我们尝试使用层次布局算法 Dagre 进行布局，它根据有向图数据中边的方向将节点进行分层。如 图 12 所示，能源的起源点（只有输出边，没有输入边的节点）大部分被放置在了第一层（最左侧），把源头放在开始观察的位置比较符合能源图的观测需求，但如核能（Nuclear）、风能（Wind）等部分起源节点并没有被放置在第一层，这是 Dagre 的计算机制导致的。因此，层次布局仍然不能完美地符合“源头 -> 中间环节 -> 最终输出”的观察过程。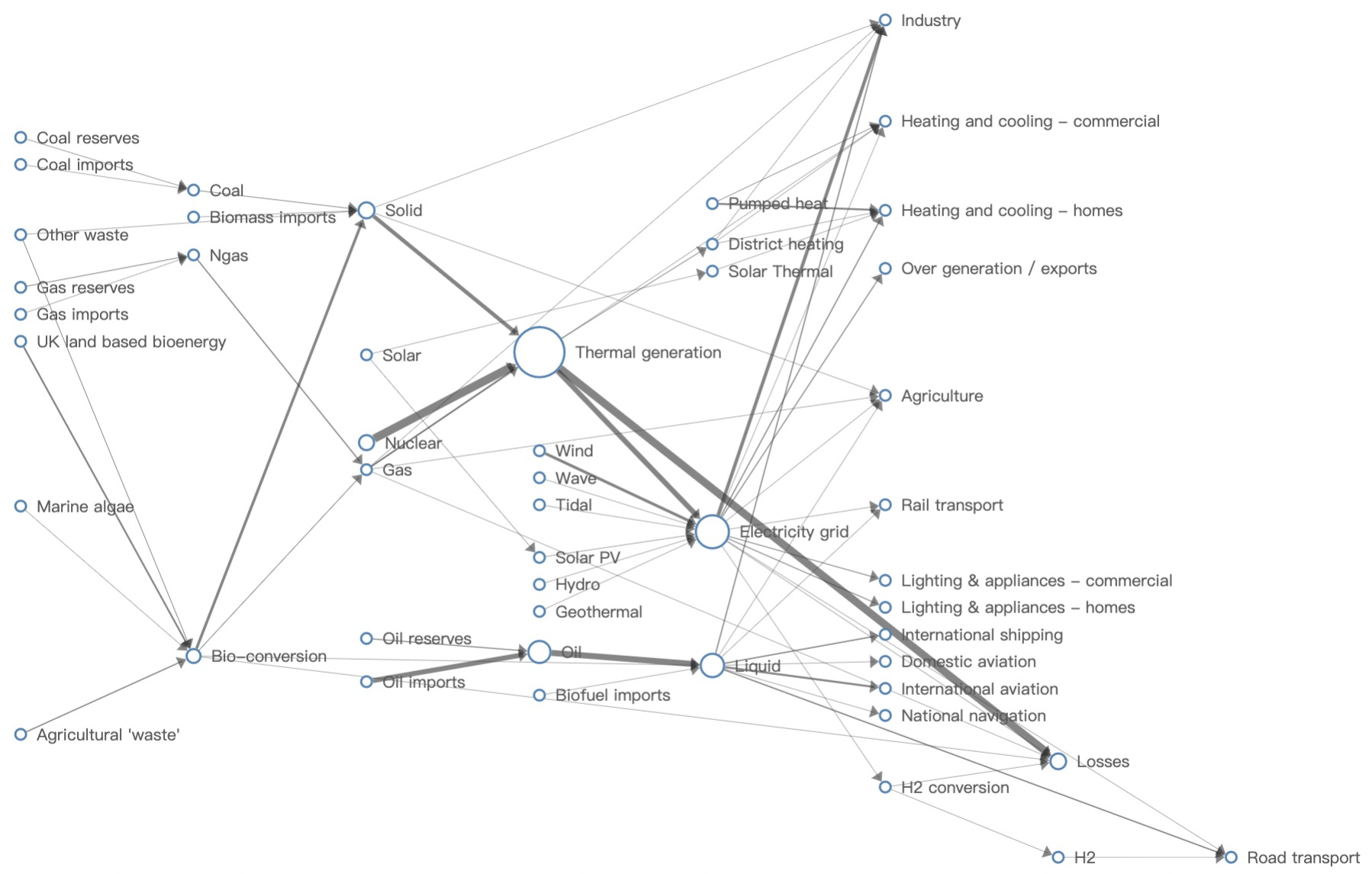

图 12. 使用 G6 内置的 Dagre 层次布局算法展示能源图。

流图 / 桑基图 —— 最终选择

（PD：有完没完了，快给我个痛快！我：喳，瞧好了您呐。）严格来说，桑基图不算是完全意义上的点线图。与流程图类似，它将自动根据边的走向对节点进行分层以表达流向（一般是从左到右），并使用高度不同的矩形代表节点，带有宽度的边代表两端点间流量，一个节点输入边宽之和或输出边宽之和等于节点的高度，从而可以映射每种流量的占比。（说起来有点抽象，看 图 13 就明白啦。）

由上文中的流程图得到启发，我们重新审视能量图可视化的需求：

• 满足“源头 -> 中间环节 -> 最终输出”的层次观测观测需求；
• 能够展示出节点、边的流量（能量值）及其占比；
• 能量的流转方向。

总而言之，能量图最重要的是表达“流”、“层次”信息。那么，流图或桑基图应该特别适用。如 图 13 所示，节点高度表示该环节总能量值，边的粗细代表其两端点之间的能量传输值。所有的起源节点被放置在第一层（最左侧），最终输出节点在最后一层（最右侧）。可以清晰探索每一条能源流的走向、环节。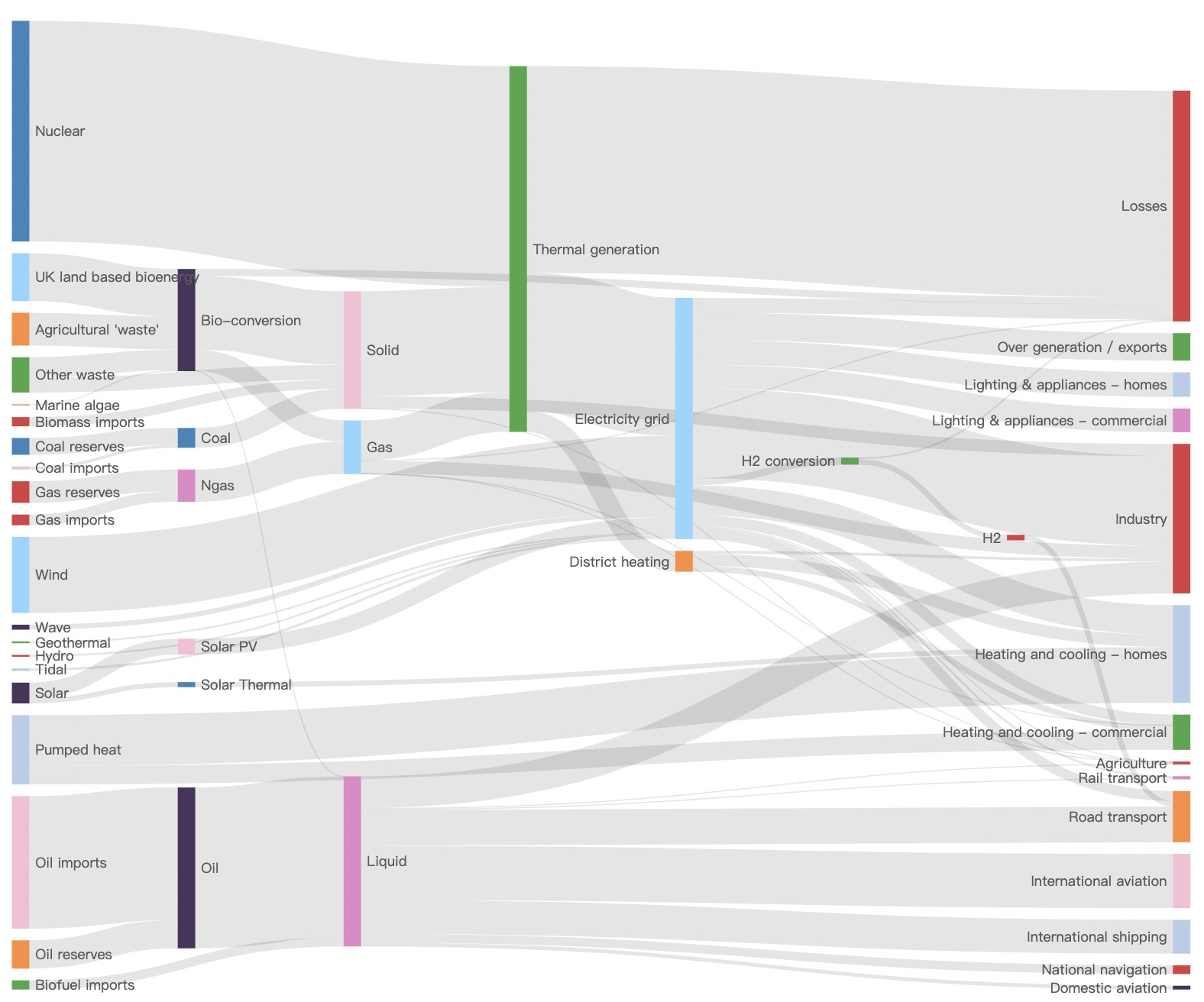

图 13. 使用 G6 绘制的能量流转桑基图。

（我：PD 大大，来分析一波吧）基于 图 13 的能量流转桑基图，可以分析：

• 根据节点大小可以发现核能（Nuclear）的能量值是所有能源源头中能量值最高的，其次是石油（Oil imports）、风能（Wind）；

• 能源最终输出中，最大的一部分竟然是被流失了（Losses）（人类真该好好思考如何提高能量转换率呢），其次是工业（Industry）、家庭采冷暖（Heating and cooling -homes）；

• 在中间环节里，热能转换（Thermal generation）的能量值最高，其次是电力网（Electricity grid）；

• 还可以发现能源可以被划分为固体（Solid）、气体（Gas）、液体（Liquid）三类，其中包含石油在内的液体占比最高，它的主要使用场景是运输（公路运输 Road transport，海运 International shipping、航运 International aviation）及工业，而气体、固体则主要用于产热与产电；

• 人类对清洁能源的使用量不高，代表潮汐能（Tidal）、太阳能（Solar）、氢气能（H2）、水电（Hydro）的节点都非常小；

• 有一种少见的能源 —— 海藻能（Marine algae）出现在了起源节点中，查阅相关资料发现这是一种绿色能源，可以用于制作海草燃料和海草油；

• …… 更多信息由您来探索啦。

结束语

点线图可视化依赖于图布局算法，应当根据数据特性、分析需求、结合终端用户的心智，在茫茫算法中选择合适的一种。图可视化不是只有力导向一种，力导向图并不能解决所有需求鸭。

两个点，一条边，就是一幅图：图可视化就是这么简单。但它又变化无穷，姿态万千：图可视化又是这样复杂。时而极简，时而繁华，时而文艺，时而张扬，这就是图可视化的魅力所在吧。

想要看到更多图可视化小知识，持续关注《Graph Visualization · 知多少》哦！

本文中的图可视化由 G6 提供支持。 G6 —— 专业的图可视化引擎。让关系数据变得简单透明，让用户获得 Insight。 G6 官网：antv.alipay.com/zh-cn/g…。欢迎关注。 GitHub：github.com/antvis/g6。欢迎 Star。

参考文献

[1] Nguyen, Quang Vinh, and Mao Lin Huang. “A space-optimized tree visualization.” IEEE Symposium on Information Visualization, 2002. INFOVIS 2002.. IEEE, 2002.
[2] Carriere, Jeromy, and Rick Kazman. “Interacting with huge hierarchies: Beyond cone trees.” Proceedings of Visualization 1995 Conference. IEEE, 1995.
[3] Herman, Ivan, et al. “Latour—a tree visualisation system.” International Symposium on Graph Drawing. Springer, Berlin, Heidelberg, 1999.
[4] Jankun-Kelly, T. J., and Kwan-Liu Ma. “MoireGraphs: Radial focus+ context visualization and interaction for graphs with visual nodes.” IEEE Symposium on Information Visualization 2003 (IEEE Cat. No. 03TH8714). IEEE, 2003.
[5] Fekete, J., et al. “Interactive poster: Overlaying graph links on treemaps.” Proceedings of the IEEE Symposium on Information Visualization Conference Compendium (InfoVis 03). 2003.
[6] Holten, Danny. “Hierarchical edge bundles: Visualization of adjacency relations in hierarchical data.” IEEE Transactions on visualization and computer graphics 12.5 (2006): 741-748.
[7] Cui, Qingguang, et al. “Measuring data abstraction quality in multiresolution visualizations.” IEEE Transactions on Visualization and Computer Graphics 12.5 (2006): 709-716.
[8] Doemel, Peter. “WebMap: a graphical hypertext navigation tool.” Computer Networks and ISDN Systems 28.1-2 (1995): 85-97.
[9] Hao, Ming C., et al. “Web-based visualization of large hierarchical graphs using invisible links in a hyperbolic space.” Working Conference on Visual Database Systems. Springer, Boston, MA, 2000.
[10] Boutin, Francois, Jérôme Thievre, and Mountaz Hascoët. “Focus-based filtering+ clustering technique for power-law networks with small world phenomenon.” Visualization and Data Analysis 2006. Vol. 6060. International Society for Optics and Photonics, 2006.
[11] Boutin, François, Jérôme Thièvre, and Mountaz Hascoët. “Multilevel compound tree–construction visualization and interaction.” IFIP Conference on Human-Computer Interaction. Springer, Berlin, Heidelberg, 2005.
[12] Purchase, Helen C., Robert F. Cohen, and Murray James. “Validating graph drawing aesthetics.” International Symposium on Graph Drawing. Springer, Berlin, Heidelberg, 1995.
[13] Eades, Peter. “A heuristic for graph drawing.” Congressus numerantium 42 (1984): 149-160.
[14] Fruchterman, Thomas MJ, and Edward M. Reingold. “Graph drawing by force‐directed placement.” Software: Practice and experience 21.11 (1991): 1129-1164.
[15] Gansner, Emden R., and Stephen C. North. “Improved force-directed layouts.” International Symposium on Graph Drawing. Springer, Berlin, Heidelberg, 1998.
[16] Eades, Peter, and Mao Lin Huang. “Navigating clustered graphs using force-directed methods.” Graph Algorithms And Applications 2. 2004. 191-215.
[17] Gajer, Pawel, Michael T. Goodrich, and Stephen G. Kobourov. “A multi-dimensional approach to force-directed layouts of large graphs.” International Symposium on Graph Drawing. Springer, Berlin, Heidelberg, 2000.
[18] Dwyer, Tim, Kim Marriott, and Michael Wybrow. “Integrating edge routing into force-directed layout.” International Symposium on Graph Drawing. Springer, Berlin, Heidelberg, 2006.
[19] Misue, Kazuo, et al. “Layout adjustment and the mental map.” Journal of Visual Languages & Computing 6.2 (1995): 183-210.
[20] Harel, David, and Yehuda Koren. “Graph drawing by high-dimensional embedding.” International symposium on graph drawing. Springer, Berlin, Heidelberg, 2002.