核心思想

通过定义图的能量，并不断迭代获取能量最小的布局。

源码

源码地址：https://github.com/mysql/mysql-workbench/blob/f7a0175471d773ddbac671d9176b13d0c6243637/modules/wb.model/src/wb_model.cpp
MySql Workbench 布局源码解读 - 图1
核心步骤：

  1. int Layouter::do_layout() {
  2.     prepare_layout_stages();
  4.     _min_energy = calc_energy();
  5.     int de0_count = 10; // de=0 count
  6.     double de = 1;      // energy delta
  7.     double prev_energy = 0;
  8.     while (de0_count > 0) {
  9.         shuffle();
  10.         de = prev_energy - _min_energy;
  11.         prev_energy = _min_energy;
  12.         if (de == 0)
  13.             --de0_count;
  14.         else
  15.             de0_count = 10;
  16.     }
  18.     // update actual figures with new coords
  19.     for (std::size_t i = 0; i < _figures.size(); ++i) {
  20.         Node &n = _figures[i];
  21.         model_FigureRef &f = n.fig;
  23.         f->left(n.x1);
  24.         f->top(n.y1);
  25.     }
  26. }
  1. 图数据初始化。
  2. 计算图能量。
  3. 移动节点位置，迭代直到找到能量最小的布局。

  4. 根据计算结果，更新节点位置。

    核心步骤

    1. 初始化

    1. void Layouter::prepare_layout_stages() {
    2.  double total_w = 0;
    3.  double total_h = 0;
    4.  // 根据节点的连接数进行排序
    5.  std::sort(_figures.begin(), _figures.end(), compare_node_links);
    7.  // reset layout
    8.  for (size_t i = 0; i < _figures.size(); ++i) {
    9.    Node &n = _figures[i];
    10.    // place all tables in some initial position
    11.    // 节点初始位置
    12.    n.move((long)_w / 4, (long)_h / 4);
    14.    // Calculate total dimensions and find max cell size.
    15.    // 计算图最小的面积。cell为节点最大的宽度和高度
    16.    total_w += n.w;
    17.    total_h += n.h;
    18.    if (_cell_w < n.w)
    19.      _cell_w = (int)n.w;
    20.    if (_cell_h < n.h)
    21.      _cell_h = (int)n.h;
    22.  }
    23.  // 单元格放大1.1倍
    24.  _cell_w = (int)(1.1 * _cell_w);
    25. }

  5. 将节点按照其边的连接数从小到大排序。

  6. 根据节点的面积叠加计算图的面积。
  7. 计算单元格的宽度和高度。（节点的最大高度和宽度）
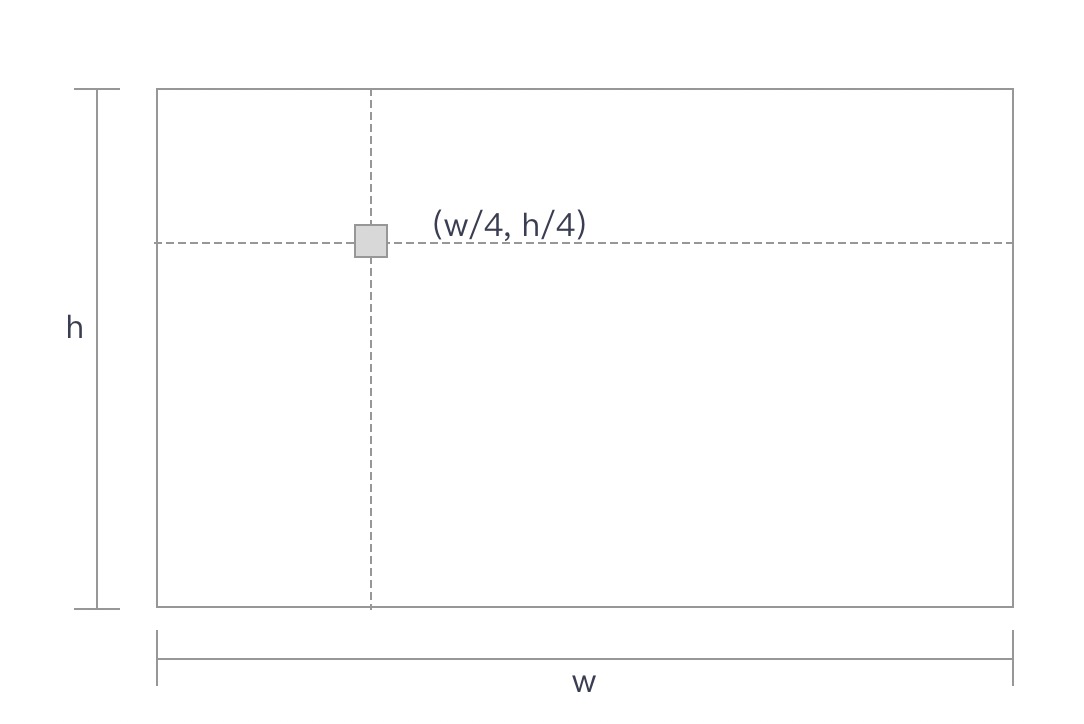
  8. 节点位置初始化，初始化位置在画布的左上角四分之一处。

MySql Workbench 布局源码解读 - 图2

2. 计算图能量

  1. double Layouter::calc_energy() {
  2.     double e = 0.0;
  4.     std::size_t size = _figures.size();
  5.     for (std::size_t i = 0; i < size; ++i) {
  6.       const Node &node = _figures[i];
  7.       // 位置在可视区之外的节点，能量加很大的一个值
  8.       if ((node.x1 < 0) || (node.y1 < 0) || (node.x2 + 20 > _w) || (node.y2 + 20 > _h))
  9.         e += 1000000000000.0;
  11.       // 计算任意两个节点之间的能量
  12.       for (std::size_t j = i + 1; j < size; ++j) {
  13.         if (j >= size)
  14.           break;
  15.         e += calc_node_pair(i, j);
  16.       }
  17.     }
  19.     return e;
  20. }

计算图整体的能量。

  1. 遍历位置在可视区之外的节点，能量增加 1,000,000,000,000。

  2. 遍历计算节点两两之间的能量，叠加到图能量中。

    3. 计算节点之间能量

    1. double Layouter::calc_node_pair(const std::size_t i1, const std::size_t i2) {
    2.  const Node *n1 = &(_figures[i1]);
    3.  const Node *n2 = &(_figures[i2]);
    4.  const bool is_linked = n1->is_linked_to(i2) || n2->is_linked_to(i1);
    6.  // 计算节点的面积，节点面积从小到大
    7.  long S1 = n1->w * n1->h;
    8.  long S2 = n2->w * n2->h;
    9.  if (S1 > S2) {
    10.    std::swap(n1, n2);
    11.    std::swap(S1, S2);
    12.  }
    14.  const long x11 = n1->x1;
    15.  const long y11 = n1->y1;
    16.  const long x12 = n1->x2;
    17.  const long y12 = n1->y2;
    19.  const long x21 = n2->x1;
    20.  const long y21 = n2->y1;
    21.  const long x22 = n2->x2;
    22.  const long y22 = n2->y2;
    24.  const long cx1 = x11 + (x12 - x11) / 2;
    25.  const long cy1 = y11 + (y12 - y11) / 2;
    26.  const long cx2 = x21 + (x22 - x21) / 2;
    27.  const long cy2 = y21 + (y22 - y21) / 2;
    29.  // Detect if nodes overlap  检查节点之间是否存在覆盖问题
    30.  const bool is_overlap = ((x12 >= x21) && (x22 >= x11) && (y12 >= y21) && (y22 >= y11));
    32.  static const double overlap_quot = 1000.0;
    34.  double e = 0.0;
    35.  double distance = 0;
    36.  if (is_overlap) {
    37.    distance = line_len2(cx1, cy1, cx2, cy2);
    39.    // calc area of overlap 计算重复区域的坐标和面积
    40.    const long sx1 = x11 > x21 ? x11 : x21;
    41.    const long sy1 = y11 > y21 ? y11 : y21;
    42.    const long sx2 = x12 < x22 ? x12 : x22;
    43.    const long sy2 = y12 < y22 ? y12 : y22;
    44.    const long dsx = sx2 - sx1;
    45.    const long dsy = sy2 - sy1;
    47.    const long Sov = dsx * dsy;
    49.    if (distance == 0.0)
    50.      distance = 0.0000001;
    52.    e = _min_dist * 1 / distance * 100 + Sov;
    53.    e *= overlap_quot;
    54.  } else {
    55.    bool is_horiz = false;
    56.    distance = distance_to_node(i1, i2, &is_horiz);
    58.    if (distance <= _min_dist) {
    59.      if (distance != 0) {
    60.        if (is_linked)
    61.          e += _min_dist + overlap_quot * 1 / distance;
    62.        else
    63.          e += _min_dist + overlap_quot * _min_dist / distance;
    64.      } else {
    65.        e += overlap_quot;
    66.      }
    67.    } else {
    68.      e += distance;
    69.      if (is_linked)
    70.        e += distance * distance;
    71.    }
    72.  }
    74.  return e;
    75. }

  3. 按照节点面积排序，节点面积小的是n1，节点面积大的是n2.

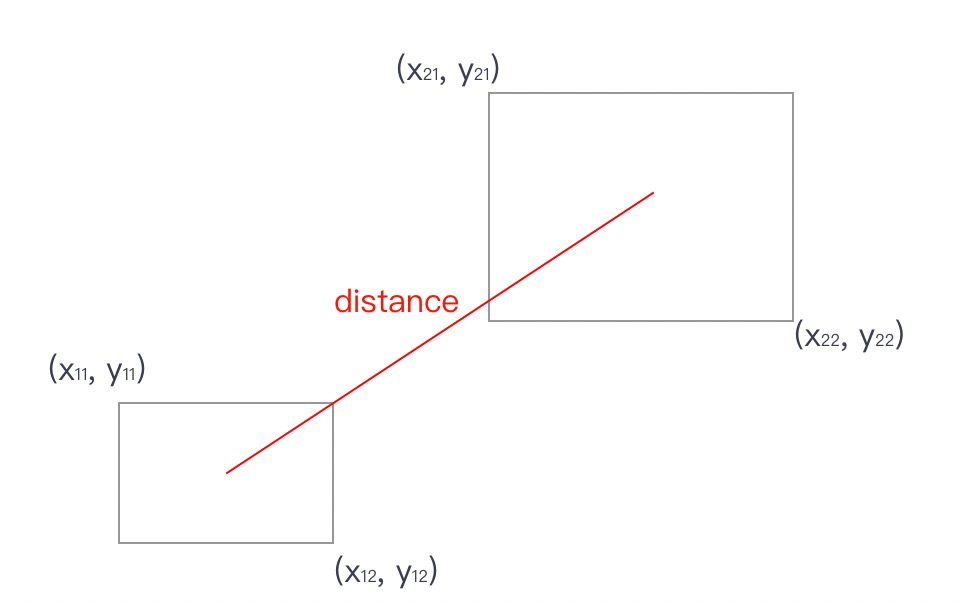
  4. 判断两个节点是否存在覆盖问题。如存在，能量增加重叠区域面积的指定倍数。并乘以固定值重叠能量1000

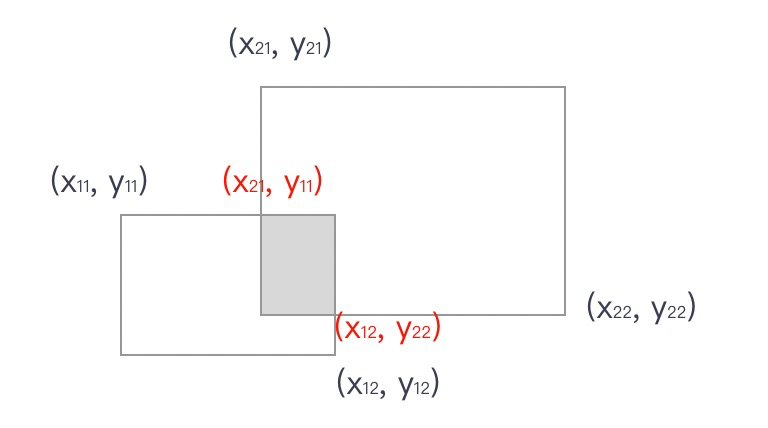
MySql Workbench 布局源码解读 - 图3

  1. 计算两个节点之间的距离 distance_to_node。
  2. 判断两个节点之间的距离是否小于指定的最小间距。如果小于，增加固定值能量除以distance。

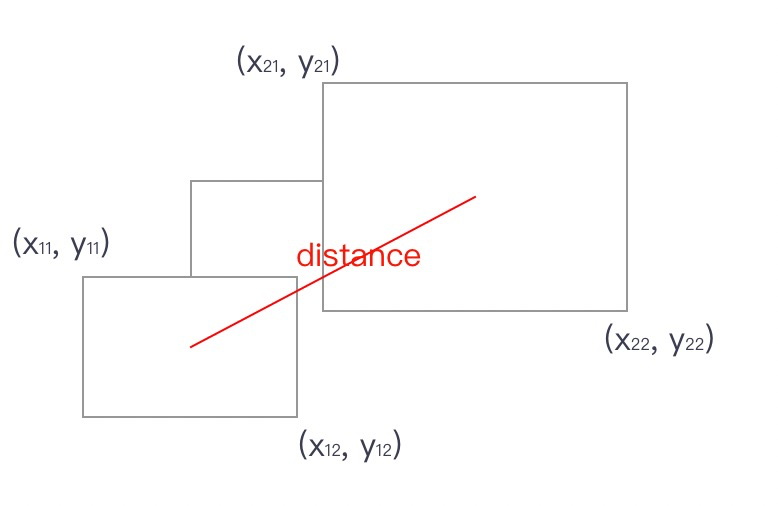
MySql Workbench 布局源码解读 - 图4

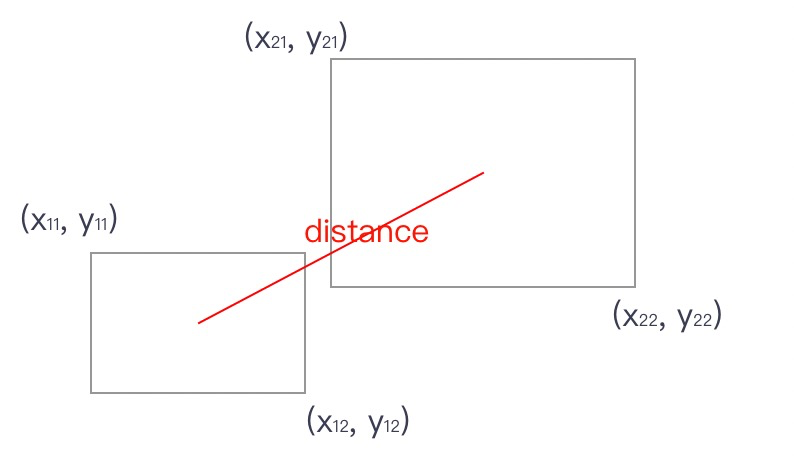
MySql Workbench 布局源码解读 - 图5

  1. 如果两个节点之间有边链接，能量值叠加节点间距离的平方。

MySql Workbench 布局源码解读 - 图6

  1. 其他情况，能量值叠加节点间距。

    4. 节点距离计算

    1. long Layouter::distance_to_node(const std::size_t i1, const std::size_t i2, bool *is_horiz) {
    2.  const Node &n1 = _figures[i1];
    3.  const Node &n2 = _figures[i2];
    4.  const long x11 = n1.x1;
    5.  const long y11 = n1.y1;
    6.  const long x12 = n1.x2;
    7.  const long y12 = n1.y2;
    9.  const long x21 = n2.x1;
    10.  const long y21 = n2.y1;
    11.  const long x22 = n2.x2;
    12.  const long y22 = n2.y2;
    14.  const long cx1 = x11 + (x12 - x11) / 2;
    15.  const long cy1 = y11 + (y12 - y11) / 2;
    16.  const long cx2 = x21 + (x22 - x21) / 2;
    17.  const long cy2 = y21 + (y22 - y21) / 2;
    18.  const long dcx = cx2 - cx1;
    19.  // 两个节点间的方位角  
    20.  const double qr = atan2((double)dcx, (double)(cy2 - cy1));
    22.  double dx = 0;
    23.  double dy = 0;
    24.  double l1 = 0;
    25.  double l2 = 0;
    26.  // 如果大于90度。l1 l2 为欧式距离
    27.  if (qr > M_PI_2) {
    28.    dy = y11 - y22;
    29.    dx = x21 - x12;
    30.    l1 = dy ? ::fabs(dy / cos(qr)) : ::fabs(dx); 
    31.    l2 = dx ? ::fabs(dx / sin(qr)) : ::fabs(dy); 
    32.  } else if (0.0 < qr && qr <= M_PI_2) {
    33.    dy = y21 - y12;
    34.    dx = x21 - x12;
    35.    if (dy > dx)
    36.      l1 = l2 = dy ? ::fabs(dy / cos(qr)) : ::fabs(dx);
    37.    else
    38.      l1 = l2 = dx ? ::fabs(dx / sin(qr)) : ::fabs(dy);
    39.  } else if (qr < -M_PI_2) {
    40.    dy = y11 - y22;
    41.    dx = -(x22 - x11);
    42.    if (dy > dx)
    43.      l1 = l2 = dy ? ::fabs(dy / cos(qr)) : ::fabs(dx);
    44.    else
    45.      l1 = l2 = dx ? ::fabs(dx / sin(qr)) : ::fabs(dy);
    46.  } else {
    47.    dy = y21 - y12;
    48.    if (abs(dcx) > (x12 - x11) / 2)
    49.      dx = x11 - x22;
    50.    else
    51.      dx = dcx;
    52.    if (dy > dx)
    53.      l1 = l2 = dy ? ::fabs(dy / cos(qr)) : ::fabs(dx);
    54.    else
    55.      l1 = l2 = (dx && qr != 0.0) ? ::fabs(dx / sin(qr)) : ::fabs(dy);
    56.  }
    58.  // printf("qr %f (cos(qr) = %f, sin(rq) = %f), l1 %li, l2 %li, dy %li, dx %li\n", qr, cos(qr), sin(qr), l1, l2, dy,
    59.  // dx);
    61.  const double aqr = ::fabs(qr);
    62.  // 判断是否水平，角度
    63.  if (is_horiz)
    64.    *is_horiz = PI_38 < aqr && aqr < PI_58;
    65.  return l1 < l2 ? (long)l1 : (long)l2;
    66. }

    在解读代码之前，先来回顾一下三角函数的计算。
    MySql Workbench 布局源码解读 - 图7
    c++中 atan2 求方位角。 其计算公式如下，其中arctan(a/b) = A ，arctan是tan的反函数。
    MySql Workbench 布局源码解读 - 图8
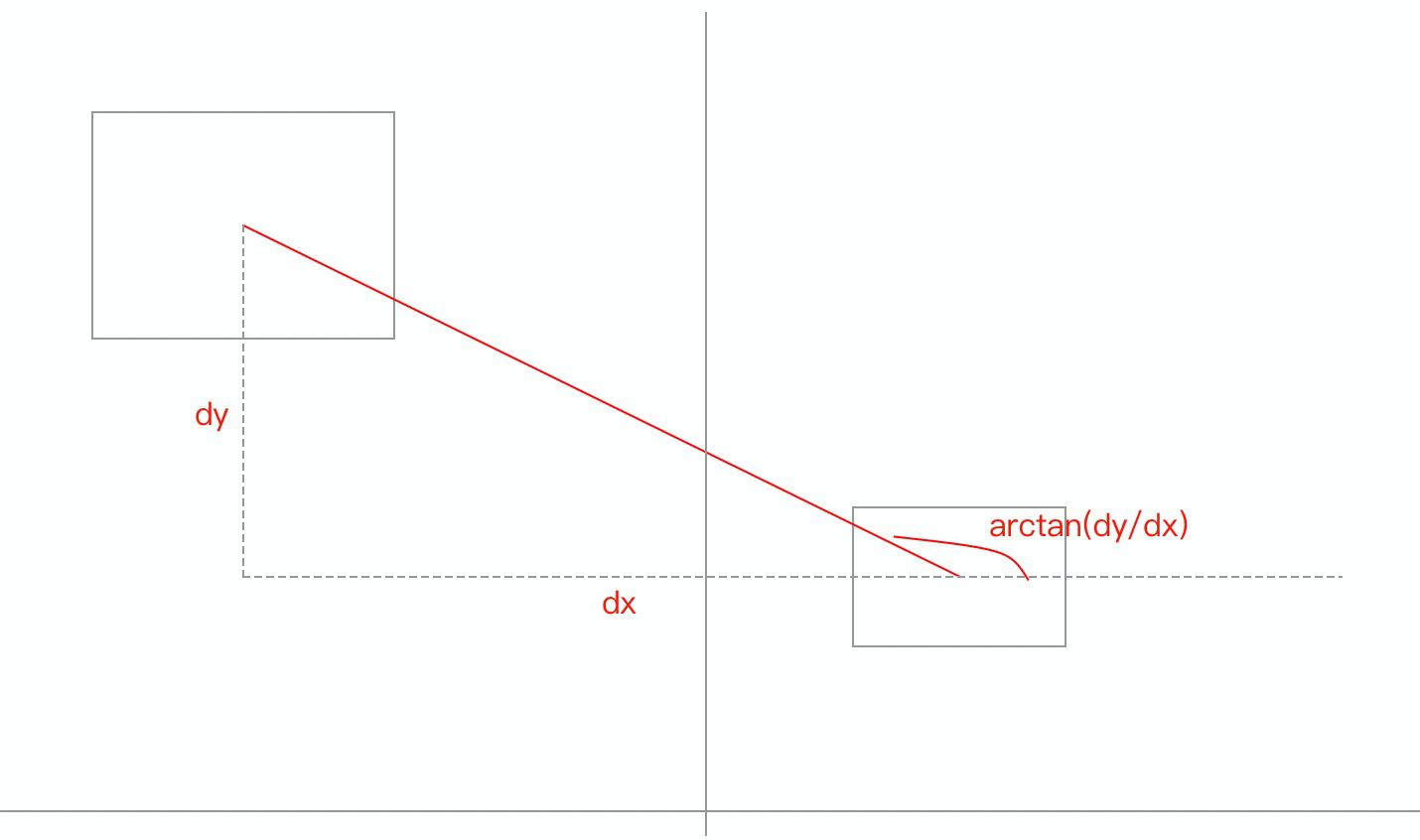
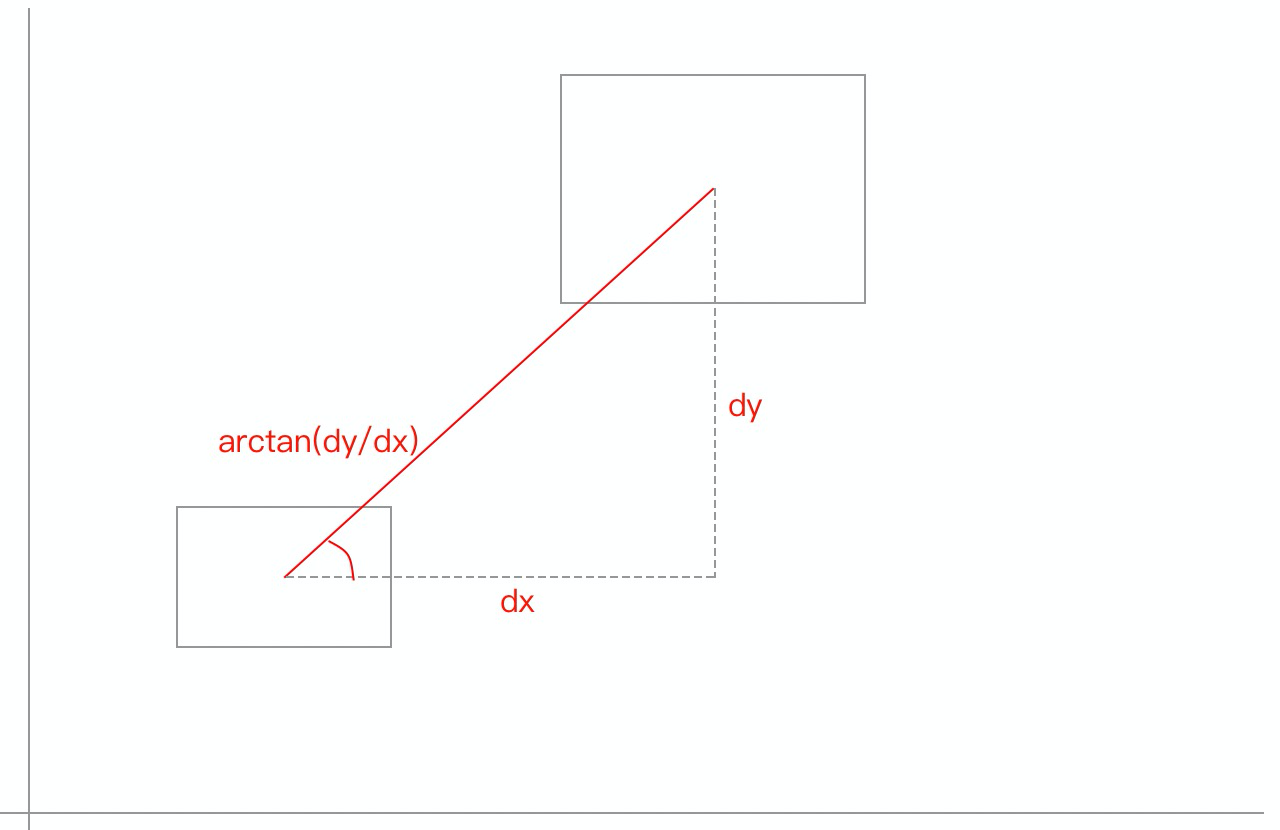
    MySql Workbench 布局源码解读 - 图9 MySql Workbench 布局源码解读 - 图10
    然后我们再回归到源码实现部分。
    情况1：角度>90。
    , 又因为

=>

=>
=>
MySql Workbench 布局源码解读 - 图11
和直接用欧拉距离对比，增加dy/dx的斜率比，可以更好的考虑整个图的长宽比。

5. 移动节点

移动节点找到可以使图能量最小的布局。

  1. bool Layouter::shuffle() {
  2.     bool found_smaller_energy = false;
  3.     // 0-5的随机数
  4.     const int step = (rand() % 5) + 1;
  6.     for (std::size_t i = 0; i < _figures.size(); ++i) {
  7.       Node &n = _figures[i];
  8.       const int wstep = _cell_w * step;
  9.       const int hstep = _cell_w * step;
  10.       double node_energy = calc_node_energy(i, n);
  12.       const int wsteps[] = {wstep, -wstep, 0, 0};
  13.       const int hsteps[] = {0, 0, hstep, -hstep};
  14.       for (int ns = sizeof(wsteps) / sizeof(int) - 1; ns >= 0; --ns) {
  15.         // 节点朝上下左右四个方向移动，找到能量最小的那个位置
  16.         n.move_by(wsteps[ns], hsteps[ns]);
  17.         // 计算移动后节点的能量
  18.         const double energy = calc_node_energy(i, n);
  19.         if (energy < node_energy) {
  20.           node_energy = energy;
  21.           found_smaller_energy = true;
  22.         } else          
  23.           n.move_by(-wsteps[ns], -hsteps[ns]);  // 回归原位
  24.       }
  25.     }
  27.     // 重新计算图整体的能量
  28.     if (found_smaller_energy)
  29.       _min_energy = calc_energy();
  31.     return found_smaller_energy;
  32. }
  1. 生成随机移动步数step。
  2. 遍历节点。计算节点的能量值
  3. 分别将节点从上下左右四个方向，分别移动wstep和hstep位置。
  4. 然后重新计算节点的能量。
  5. 如果节点能量有变小，则标记found_smaller_energy 为true，表示找到了更合适的布局。否则，节点位置进行回退。
  6. 返回found_smaller_energy。

节点能量计算方法：和剩余的节点的能量之和。

  1. double Layouter::calc_node_energy(const std::size_t node_i, const Node &node) {
  2.     double e = 0.0;
  4.     if ((node.x1 < 0) || (node.y1 < 0) || (node.x2 + 20 > _w) || (node.y2 + 20 > _h))
  5.       e += 1000000000000.0;
  7.     for (std::size_t i = 0; i < _figures.size(); ++i) {
  8.       if (node_i != i)
  9.         e += calc_node_pair(node_i, i);
  10.     }
  11.     return e;
  12. }

思考

和之前看的正交布局相关论文相比，这个算法的实现还是比较简单的。存在问题：

  1. 在判断是否最优值的时候，仅仅判断了此次计算结果和上次计算结果是否一致，容易导致产生局部最优解。
  2. 一次迭代的时间复杂度过高，nnn。
  3. 节点重叠的问题，只在能量计算中考虑，所以并不能完全避免结果中没有重叠的问题。
  4. 节点移动距离，单元格是按照最大的节点来定的。这样会产生稀疏图。