原文链接：https://github.com/phenomLi/Blog/issues/29

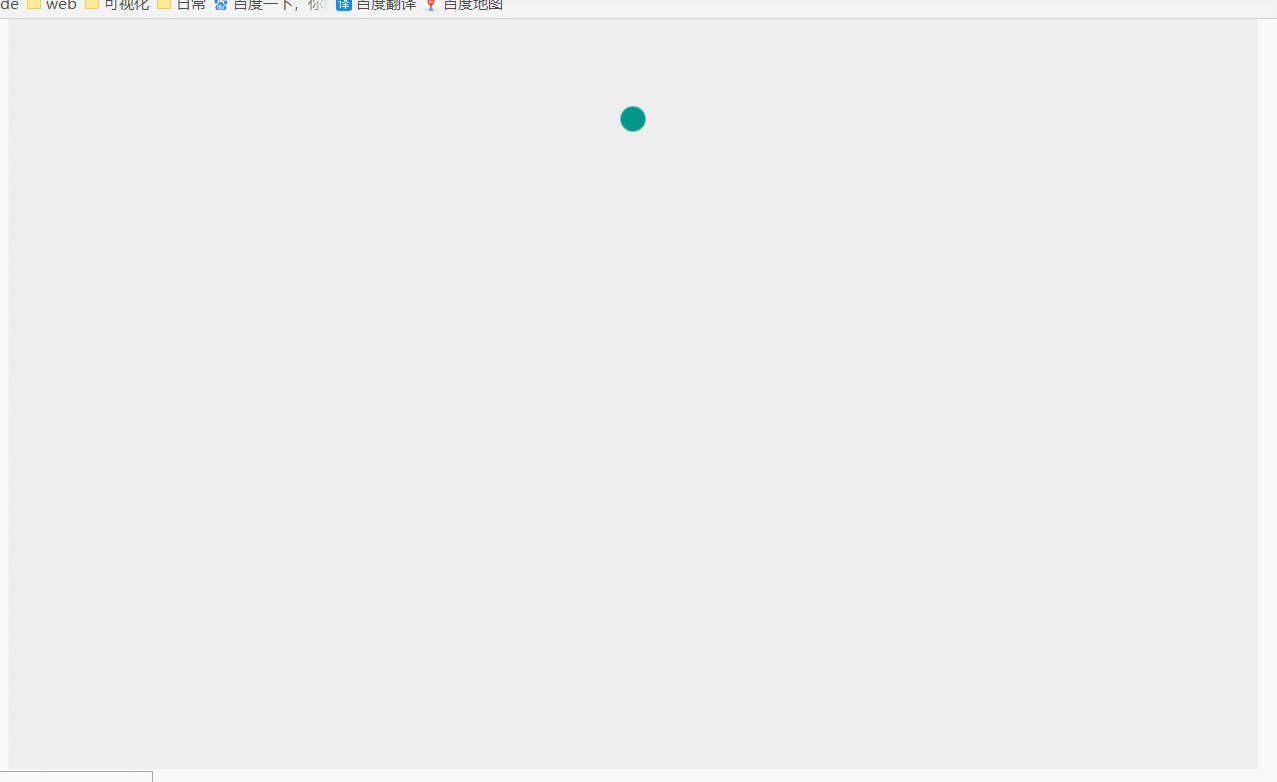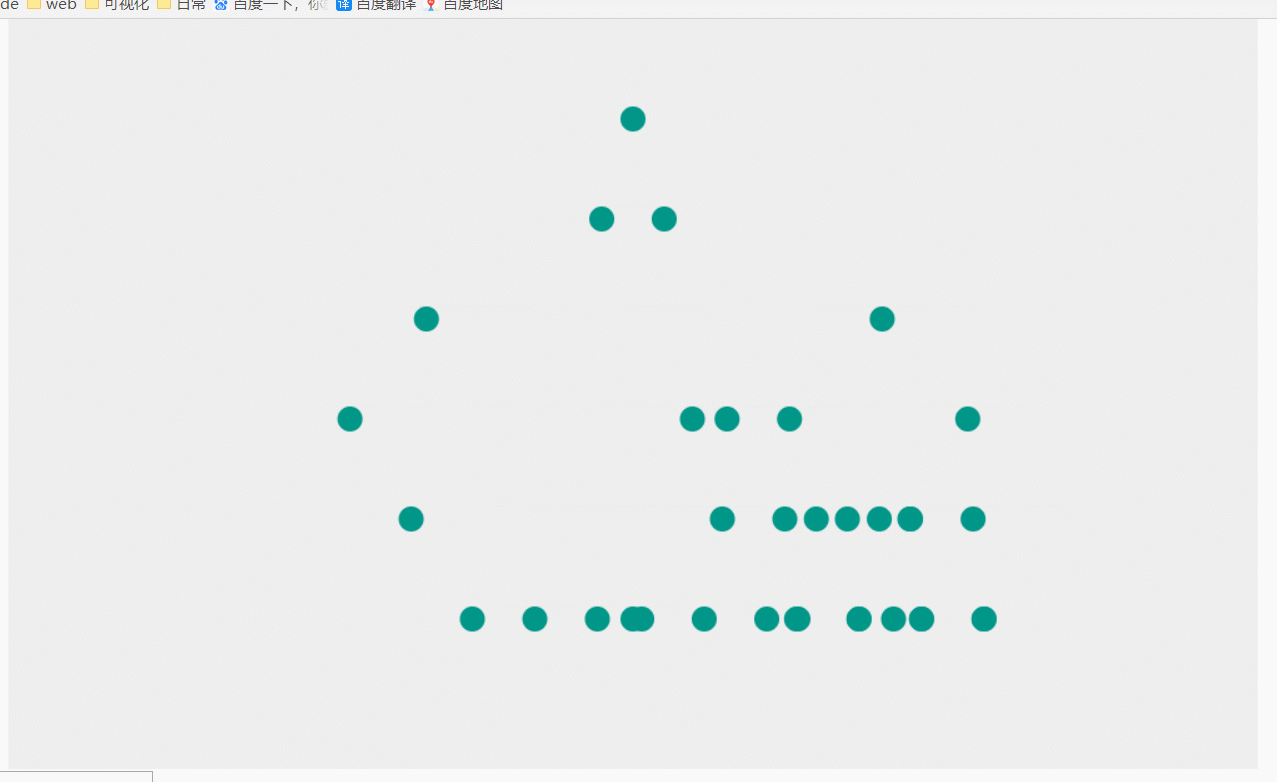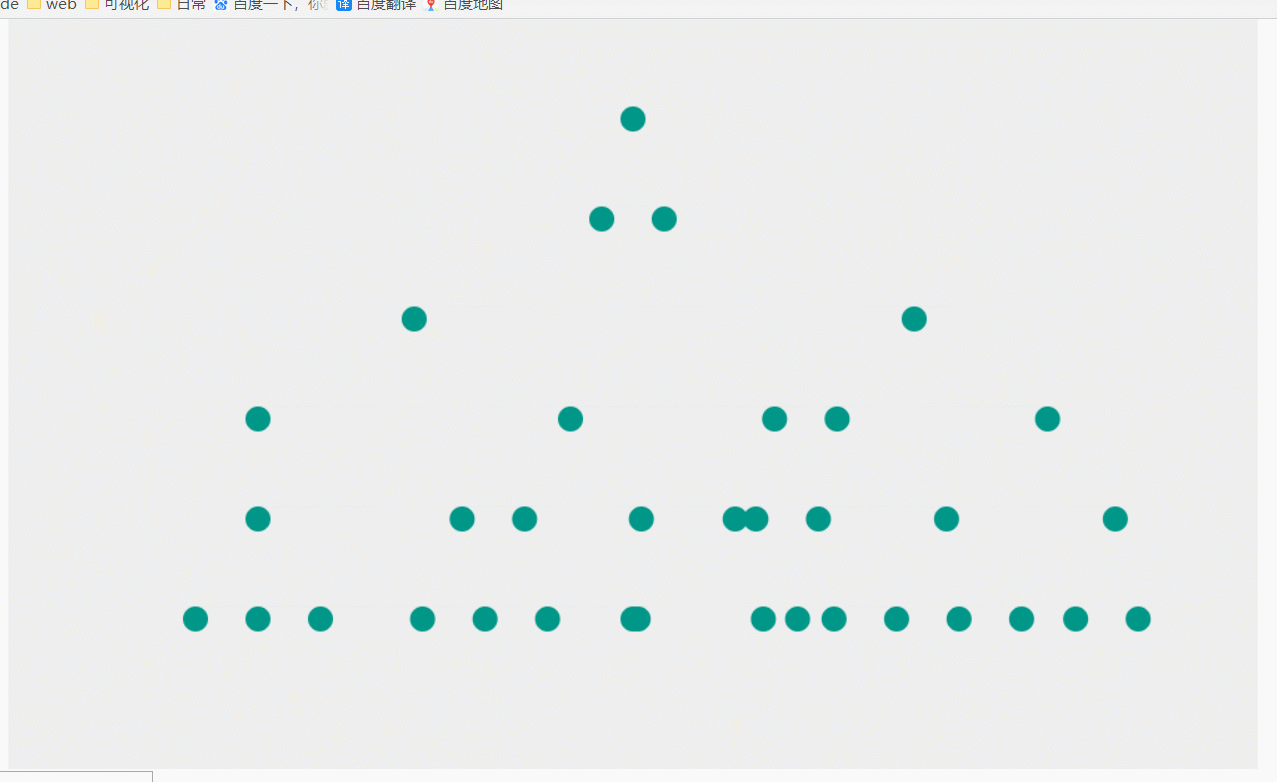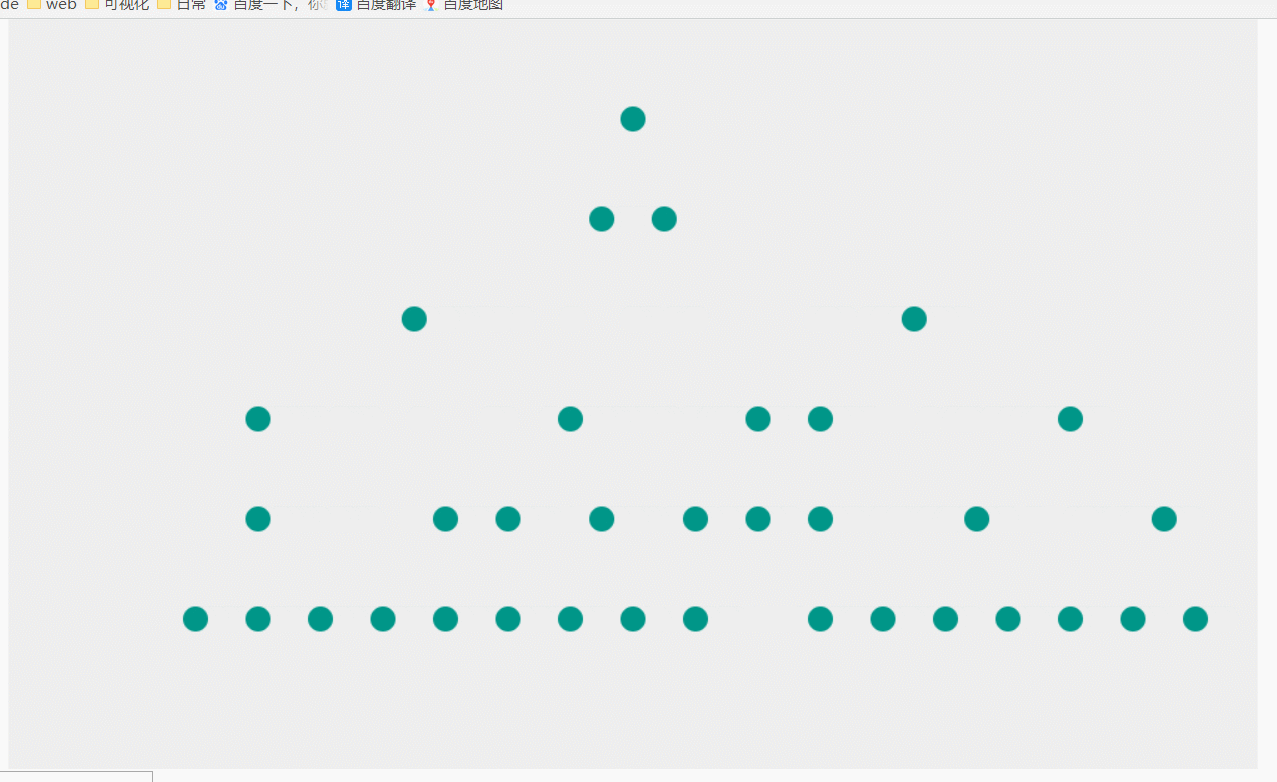
上个星期看可视化相关的论文，看到一篇介绍了一种树形结构布局算法的论文，算法效果图是这样子的：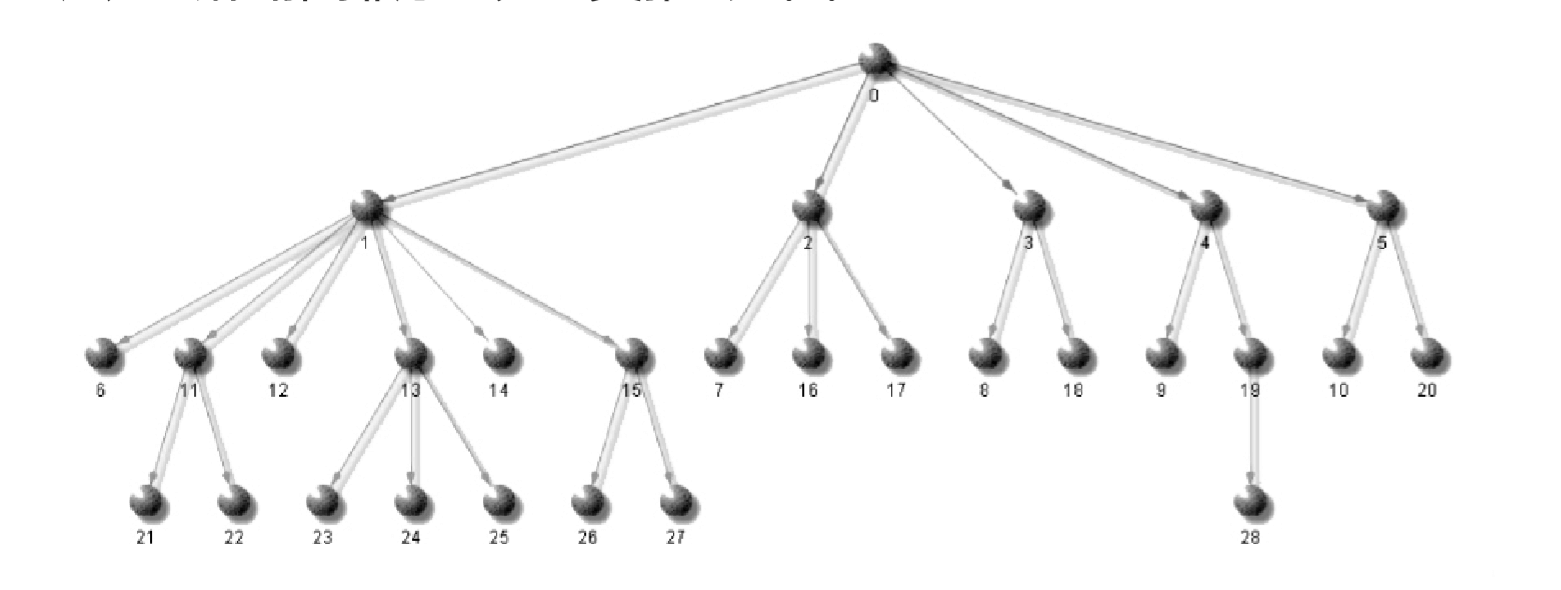
image.png
该布局的规则是：子节点相对于父节点成等腰排列，即根节点位于叶子节点两端距离上方正中间。在所有节点不重叠的情况下相邻节点间距相等，所有节点均不能重叠。其次，算法应适应于任意宽度，任意深度的树。这个布局较为美观，而且空间利用率较高。

传统的树形布局通常将子节点按照兄弟节点的最大宽度分开（一个节点的最大宽度即以该节点为根的树所占的最大宽度）。这样做虽然代码上容易实现，只要在每个节点保存该子树的最大宽度即可，但是视觉上不够美观，比较浪费空间。在某些传统布局甚至限制子节点的数目。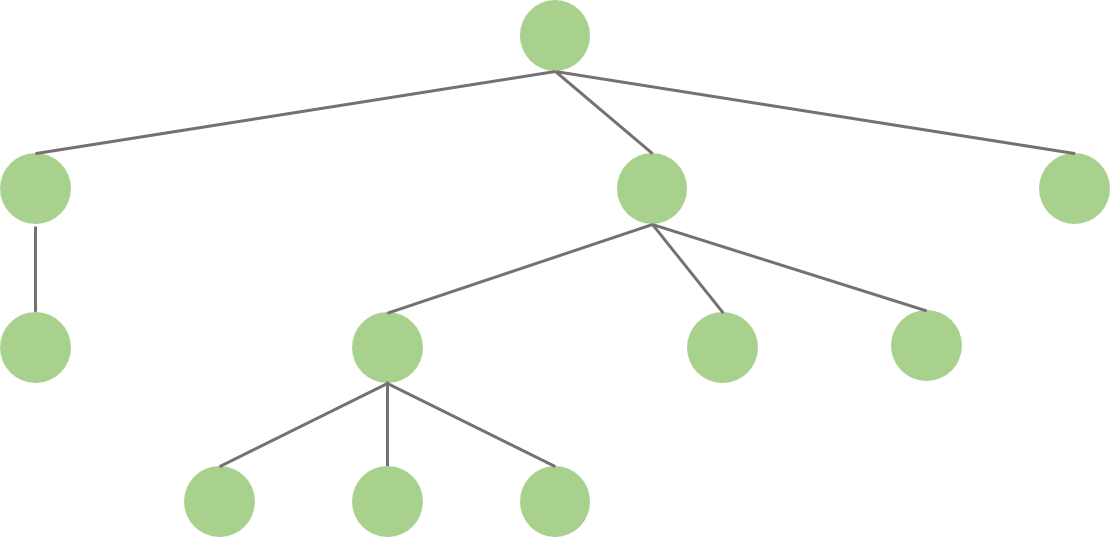
image.png
而这种布局与传统的树形布局有很大不同，它做到了在布局上节点与节点尽可能地紧凑，而且始终保持对称性和任意子节点数目。

构思

论文中只是介绍了布局的一些特点和优势，对于具体实现的思路细节并没有过多提及，说实话我第一次看到论文中的效果图，我感觉应该实现起来并不会很难，但是当时我并没有认真思考。之后隔离一天，准备动手写时我发现我被打脸了，要实现该布局，其实没有这么简单。。。。

首先，假如你有一棵树，你要将每个节点摆到正确的位置，你会发现从根往下开始一次遍历布局不行的，因为父节点的位置要根据子节点的位置而定，子节点为了避免交叉重叠，会相互隔得很开，父节点为了保持对称性，也会发生移动。而从底部往上一次遍历布局同样也行不通，因为子节点也要跟着父节点走，父节点位置改变了扫描过的子节点也需要移动。

所以，可以得出结论，只进行一次遍历是无法完成布局的（光是这点我就想了一个下午才相通，我太蔡了。。）。之后我又认真地想了两天，没错，是整整两天，没有写代码，就光想思路，终究有所收获。下面简单描述我的思路：

  1. 首先，我们从上往下，先根据相邻节点间地最小间距 nodeInterval和父子节点间地间距 yInterval对树进行第一次布局。由于初始状态所有节点的坐标都是未知的，我们不妨把所有节点的坐标先都设置为(0，0) 。从根节点开始。人为设定好根节点的坐标 ，然后将根节点的子节点挂在根节点下，且子节点分布在根节点的yInterval高度下方，子节点彼此间距为nodeInterval且相对于根节点对称分布。递归进行此步骤，直到所有的节点都布局好。

  2. 然后，我们需要一个hashTree，用作将树保存到一个按层次分别的线性表中。我们将树转换到hashTree。效果图中的树对应hashTree如下：

    1. /**
    2. * layer [
    3. *   0  [ node(0) ], 
    4. *   1  [ node(1), node(2), node(3), node(4), node(5) ],
    5. *   2  [ node(6), node(7), node(8), node(9), node(10), node(11), node(12), node(13), node(14), node(15), node(16), node(17), node(18), node(19), node(20) ],
    6. *   3  [ node(21), node(22), node(23), node(24), node(25), node(26), node(27), node(28) ]
    7. * ]
    8. */

  3. 从最低层开始从下往上按层遍历hashTree，检测相邻的节点。假设n1，n2为相邻的一对节点，n1的在线性表的下标小于n2。检测n1，n2是否重叠。如果发生重叠，则左边不动，整体往右进行调整。但调整的不是n2节点，而是“与n1的某个祖先节点为兄弟节点的n2的祖先节点”。为什么呢？后面我再解释。

  4. 上面已经提到了。每移动完一个节点，其父节点都会失去对称性，所以要进行调整。但我们不动父节点，只通过往左移动子节点来恢复对称性。原理如图示：

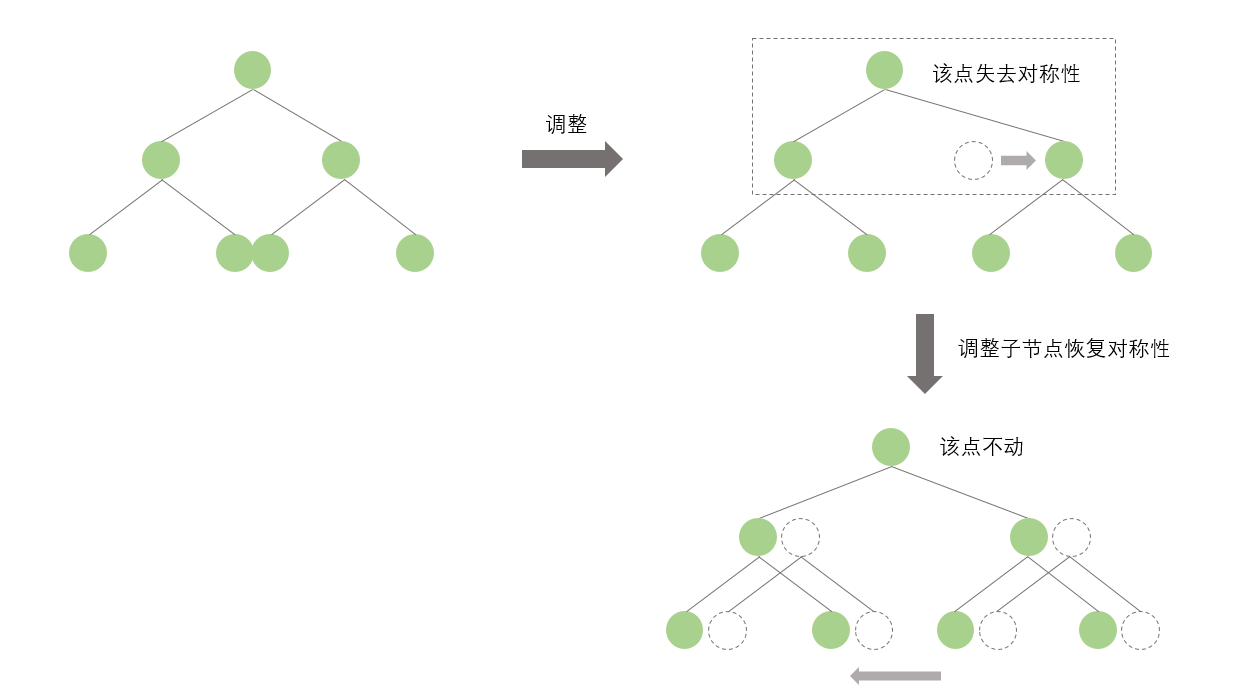
image.png

  1. 每次恢复对称性后，有某些子节点又会发生重叠现象，所以这时要回到底层重新开始扫描。
  2. 重复3，4，5步骤，直到所有重叠都被消除，布局完成。

下面说说一些细节问题：

  • 什么是“与n1的某个祖先节点为兄弟节点的n2的祖先节点”，为什么要移动它？

请看下图：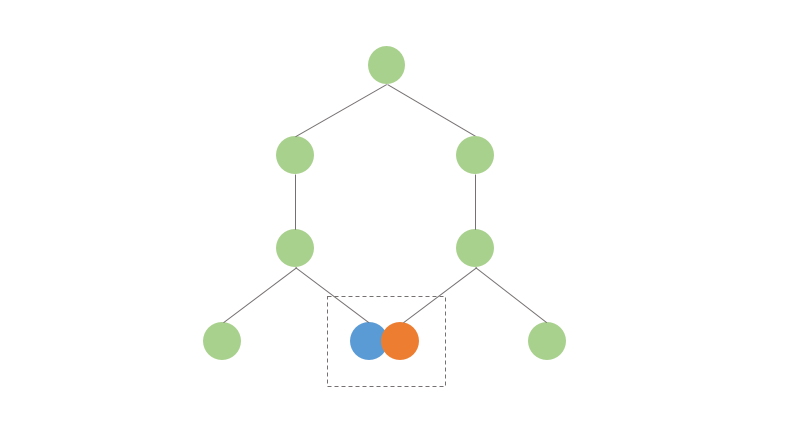
image.png
框中的两个相邻节点发生了重叠，其中蓝色为n1，橙色为n2。如果这时单纯往右地移动n2，会发现n2所在的子树发生了形变，因为n2的父节点失去了对称性，算法接下来会对该父节点进行对称性恢复。然而根据步骤4的规则，n2极其兄弟节点会往左移动，这时n1，n2会重新发生重叠。虽说经过多次迭代后n2始终会到达正确的位置，但是这不是最优解。
image.png
最优解是移动红色的节点及以该节点为根的整棵子树，即框中的所有节点，因为这样只会失去红色节点的父节点的对称性，后续只需调整那一个节点即可。其中红色节点就是“与n1的某个祖先节点为兄弟节点的n2的祖先节点”。

  • 相邻节点重叠如何判定？
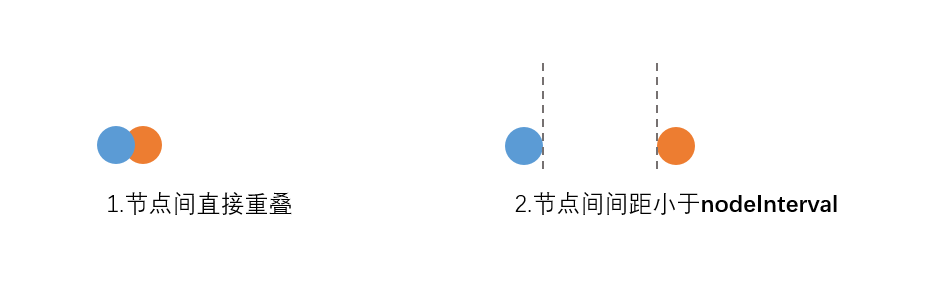
    两种情况判断为重叠：
    1.节点直接重叠；2.节点间距离小于最小距离，即nodeInterval。如下图：

image.png
以上就是我思路的全部内容，很多很长很复杂，花了我差不多整整 3 天，才把他们捋清楚。可能有一些细节还表达得不是很清楚。

为此，我还制作了一个布局过程的动态可视化动画：
tree.gif

代码实现

码代码 + debug又花了3天多，毕竟想是一回事，写又是另一回事，还踩了不少坑。

首先我们定义节点的类型，很简单：

  1. // 节点类
  2. export class Node {
  3.     // 存放节点数据
  4.     public data: any;
  6.     // 父节点
  7.     public parent: Node;
  8.     // 孩子节点
  9.     public child: Node[];
  11.     // 节点所在的层级
  12.     public layer: number;
  13.     // 节点在层级的位置
  14.     public index: number;
  15.     // 横坐标
  16.     public x: number;
  17.     // 纵坐标
  18.     public y: number;
  20.     // 初始横坐标
  21.     public ox: number;
  23.     constructor(data: any, parent: Node, layer: number, index: number, x: number, y: number) {
  24.         this.data = data;
  25.         this.parent = parent;
  26.         this.layer = layer;
  27.         this.index = index;
  28.         this.x = x;
  29.         this.y = y;
  31.         this.ox = x;
  32.         this.child = [];
  33.     }
  34. }

其中ox的作用是用作保存节点上一次布局完成的坐标，那么下一次布局完成时就可以对比ox和x是否发生了改变，对视图进行部分更新。这不是必须的，只是一种优化手段。

接下来我们可以编写树的主类：

  1. // 树的主类
  2. export class Tree {
  3.     // 根节点
  4.     public root: Node;
  5.     // 节点数
  6.     public count: number;
  8.     // 一个保存树层次结构的hashtree
  9.     private hashTree: Array<Node[]>;
  10.     // 渲染请求计数器
  11.     private renderRequestCount: number;
  12.     // 渲染执行计数器
  13.     private renderCount: number;
  15.     // 根节点横坐标
  16.     private rootX: number;
  17.     // 根节点纵坐标
  18.     private rootY: number;
  19.     // 父子节点的垂直间距
  20.     private yInterval: number;
  21.     // 节点间的水平最小间距
  22.     private nodeInterval: number;
  23.     // 节点的宽度
  24.     private nodeWidth: number;
  25.     // 节点的高度
  26.     private nodeHeight: number;
  28.     constructor() {
  29.         this.count = 0;
  31.         this.nodeWidth = 20;
  32.         this.nodeHeight = 20;
  33.         // 因为节点间的距离是从节点的中心距离计算的，所以为了方便计算，加上2*(节点宽度/2)即一个节点宽度
  34.         this.nodeInterval = 30 + this.nodeWidth;
  35.         // 同理上面
  36.         this.yInterval = 60 + this.nodeHeight;
  38.         this.rootX = 400;
  39.         this.rootY = 80;
  41.         this.hashTree = [];
  42.         this.renderRequestCount = this.renderCount = 0;
  44.         // 创建一个节点到根节点（createNode函数代码省略）
  45.         this.root = this.createNode();
  46.     }
  48.     /**
  49.      * 核心函数：布局调整函数
  50.      */
  51.     layout() {
  52.         // 正推布局，从根节点开始，按照节点的水平垂直间距布局整棵树
  53.         this.layoutChild(this.root);
  54.         // 回推布局，从最底层开始，往上检索，查找重叠节点，调整优化树的布局
  55.         this.layoutOverlaps();
  56.     }
  58.     /**
  59.      * 找出与node1的某个祖先节点为兄弟节点的node2的祖先节点
  60.      * @param node1 
  61.      * @param node2 
  62.      */
  63.     findCommonParentNode(node1: Node, node2: Node): Node {
  64.         // 若node1和node2为兄弟节点，返回node2
  65.         if(node1.parent === node2.parent) {
  66.             return node2;
  67.         }
  68.         // 否则，递归往上寻找
  69.         else {
  70.             return this.findCommonParentNode(node1.parent, node2.parent);
  71.         }
  72.     }
  74.     /**
  75.      * 水平位移整棵树
  76.      * @param node 该树的根节点
  77.      * @param x 要移动到的位置
  78.      */
  79.     translateTree(node: Node, x: number) {
  80.         // 计算移动的距离
  81.         let dx = x - node.x;
  82.         // 更新节点的横坐标
  83.         node.x = x;
  85.         // 位移所有子节点
  86.         for(let i = 0; i < node.child.length; i++) {
  87.             this.translateTree(node.child[i], node.child[i].x + dx);
  88.         }
  89.     }
  91.     /**
  92.      * 回推函数
  93.      */
  94.     layoutOverlaps() {
  95.         // 外层循环，扫描hashtree，从最底层开始往上
  96.         for(let i = this.hashTree.length - 1; i >= 0; i--) {
  97.             // 获取当前层
  98.             let curLayer = this.hashTree[i];
  100.             // 内层循环，遍历该层所有节点
  101.             for(let j = 0; j < curLayer.length - 1; j++) {
  102.                 // 获取相邻的两个节点，保存为n1，n2
  103.                 let n1 = curLayer[j], n2 = curLayer[j + 1];
  105.                 // 若n1，n2有重叠
  106.                 if(this.isOverlaps(n1, n2)) {
  107.                         // 计算需要移动距离
  108.                     let dx = n1.x + this.nodeInterval - n2.x,
  109.                         // 找出与n1的某个祖先为兄弟节点的n2的祖先
  110.                         node2Move = this.findCommonParentNode(n1, n2);
  112.                     // 往右移动n2
  113.                     this.translateTree(node2Move, node2Move.x + dx);
  114.                     this.centerChild(node2Move.parent);
  116.                     // 移动后下层节点有可能再次发生重叠，所以重新从底层扫描
  117.                     i = this.hashTree.length;
  118.                 }
  119.             }
  120.         }
  121.     }
  123.     /**
  124.      * 居中所有子节点
  125.      * @param parent 父节点：按照该父节点的位置，居中该父节点下的所有子节点
  126.      */
  127.     centerChild(parent: Node) {
  128.         // 要移动的距离
  129.         let dx = 0;
  131.         // 父节点为null，返回
  132.         if(parent === null) return; 
  134.         // 只有一个子节点，则只要将该子节点与父节点对齐即可
  135.         if(parent.child.length === 1) {
  136.             dx = parent.x - parent.child[0].x;
  137.         }
  139.         // > 1 的子节点，就要计算最左的子节点和最右的子节点的距离的中点与父节点的距离
  140.         if(parent.child.length > 1) {
  141.             dx = parent.x - (parent.child[0].x + (parent.child[parent.child.length - 1].x - parent.child[0].x)/2);
  142.         }
  144.         // 若要移动的距离不为0
  145.         if(dx) {
  146.             // 将所有子节点居中对齐父节点
  147.             for(let i = 0; i < parent.child.length; i++) {
  148.                 this.translateTree(parent.child[i], parent.child[i].x + dx);
  149.             }
  150.         }
  151.     }
  153.     /**
  154.      * 正推布局函数，将当前节点的所有子节点按等间距布局
  155.      * @param node 当前节点
  156.      */
  157.     layoutChild(node: Node) {
  158.         // 若当前节点为叶子节点，返回
  159.         if(node.child.length === 0) return;
  160.         else {
  161.             // 计算子节点最左位置
  162.             let start = node.x - (node.child.length - 1)*this.nodeInterval/2;
  164.             // 遍历子节点
  165.             for(let i = 0, len = node.child.length; i < len; i++) {
  166.                 // 计算当前子节点横坐标
  167.                 let x = start + i*this.nodeInterval;
  169.                 // 移动该子节点及以该子节点为根的整棵树
  170.                 this.translateTree(node.child[i], x);
  171.                 // 递归布局该子节点
  172.                 this.layoutChild(node.child[i]);
  173.             }
  174.         } 
  175.     }
  177.     /**
  178.      * 判断重叠函数
  179.      * @param node1 左边的节点
  180.      * @param node2 右边的节点
  181.      */
  182.     isOverlaps(node1: Node, node2: Node): boolean {
  183.         // 若左边节点的横坐标比右边节点大，或者两节点间的间距小于最小间距，均判断为重叠
  184.         return (node1.x - node2.x) > 0 || (node2.x - node1.x) < this.nodeInterval;
  185.     }
  187.     /**
  188.      * 更新需要更新的节点
  189.      * @param node 
  190.      */
  191.     patch(node: Node) {
  192.         // 若节点的当前位置不等于初始位置，则更新
  193.         if(node.x !== node.ox) {
  194.             // 渲染视图（根据你所使用的渲染库而定，这句只是伪代码） 
  195.             updateViewOnYourRenderer();
  197.             // 更新节点的初始位置为当前位置
  198.             node.ox = node.x;
  199.         }
  201.         // 递归更新子节点
  202.         for(let i = 0; i < node.child.length; i++) {
  203.             this.patch(node.child[i]);
  204.         }
  205.     }
  207.     /**
  208.      * 更新视图
  209.      */
  210.     update() {
  211.         this.renderRequestCount++;
  213.         // 异步更新
  214.         requestAnimationFrame(() => {
  215.             this.renderCount++;
  217.             if(this.renderCount === this.renderRequestCount) {
  218.                 this.layout();
  219.                 this.patch(this.root);
  221.                 this.renderCount = this.renderRequestCount = 0;
  222.             }
  223.         });
  224.     }
  225. }

最终的视图渲染呈现取决于你用的渲染库，我用的是我自己开发的 Renderer，但是我删去了相关代码。

由于篇幅问题，我这里删去了一些不重要的内容，只保留了核心的代码。一些比如节点的创建与删除，把节点插入到hashTree，从hashTree删除节点的代码我都删去了，因为这些都不是核心内容。

我在这里真的要称赞一下我自己，你们看其他人哪有像我这样，几乎每一行代码都有详细注释的，这就是态度！

效果展示

首先模仿一下论文的效果图。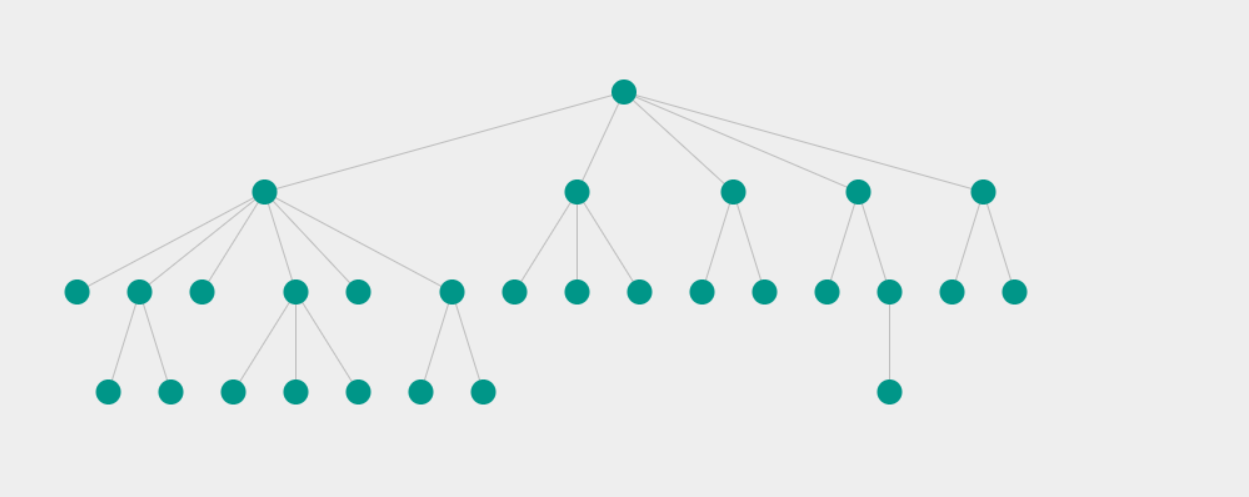
image.png

新增节点
add.gif
删除节点
del.gif