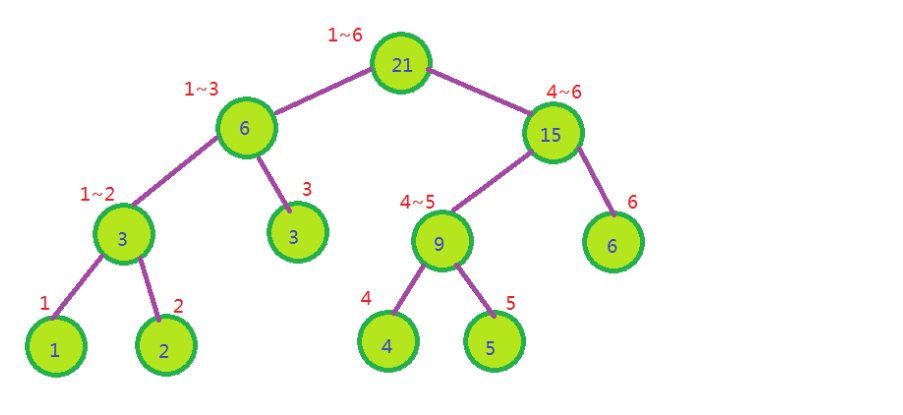
复杂度

修改和查询的时间复杂度都降到

长啥样？

长得和二叉树挺像的
image.png

性质

每个父节点都是他的两个子节点值的和

咋用

看看这个图，补上几个子节点，发现就会变成 完全二叉树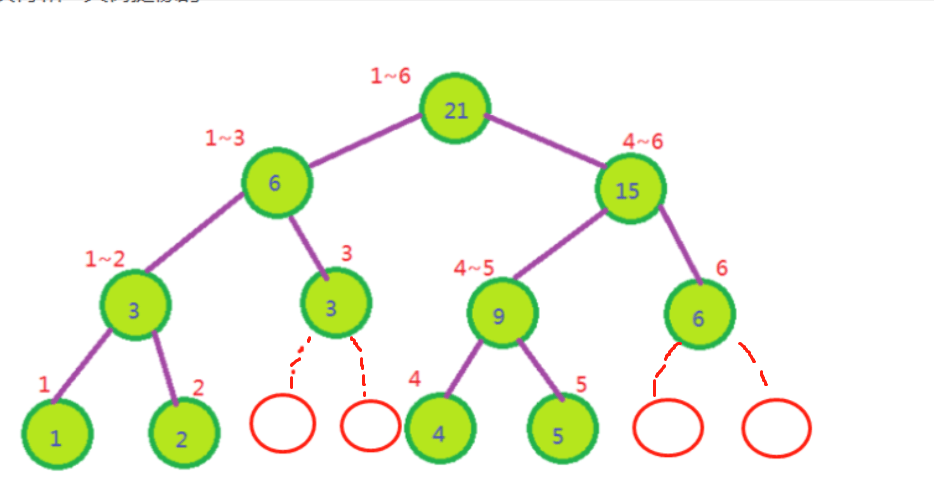
image.png
那么，我们就可以直接用数组来存储这个玩意。
根节点编号为 n ，那么它的左子树编号为 2n , 它的右子树编号为 2n + 1 。

准备

  1. #include <iostream>
  2. #include <cstring>
  3. #include <algorithm>
  4. using namespace std;
  5. #define ll long long
  6. const int N = 100010;
  8. ll arr[N] = {0},tree[4*N] = {0};//arr 为存储数据的数组， tree 是存线段树的数组

创造数组这里要注意一下，一般为了防爆，线段树数组空间要开数据数组的四倍

建树

build

  1. void build(int node, int start, int end){//建树函数，参数分别为 根节点、左右区间范围
  2.     if(start == end){//如果两边相等，说明已经到了叶节点
  3.         tree[node] = arr[start];//根节点就填入数据数组的值
  4.         return;//递归边界
  5.     }
  7.     //依据完全二叉树的性质得到左右子节点编号
  8.     int leftnode = node * 2;
  9.     int rightnode = node * 2 + 1;
  11.     //从中间分为两份，左右分别建树
  12.     int mid = (start + end) / 2;
  13.     build(leftnode, start, mid);
  14.     build(rightnode, mid + 1, end);
  16.       //根节点的值 = 左根节点的值 + 右根节点的值 
  17.     tree[node] = tree[leftnode] + tree[rightnode];
  18. }

更新树

update

  1. //修改操作，参数分别为根节点、左右区间范围、要修改的节点的编号、要改为多少的值
  2. void update(int node, int start, int end, int id, int val){
  3.     if(start == end){//递归边界，找到叶节点
  4.         tree[node] += val;//修改 node 节点的值
  5.         return;
  6.     }
  8.     int leftnode = node * 2;
  9.     int rightnode = node * 2 +1;
  10.     int mid = (start + end) / 2;
  12.     if(id >= start && id <= mid)//如果要改的地方在左半边
  13.         update(leftnode, start, mid, id, val);
  14.     else //否则
  15.         update(rightnode, mid + 1, end, id, val);
  17.     tree[node] = tree[leftnode] + tree[rightnode];//父节点更新
  18. }

区间求和

query

  1. //求和 [l,r] 区间
  2. int query(int node, int start, int end, int l, int r){
  3.     //要求和的区间已经包含当前的部分了
  4.     /*例子：
  5.     如 当前在 [1,3], 要求 [1,5], 则需要[1,3] + [4,5]
  6.     那么就直接返回建树时算好的 [1,3] 的和
  7.     */
  8.     if(l <= start && r >= end) 
  9.         return tree[node];
  11.     int leftnode = node * 2;
  12.     int rightnode = node * 2 + 1;
  13.     int mid = (start + end) / 2;
  14.     int sum = 0;//待会要返回的 和
  16.     if(l < mid) //如果要求和的区间包含中点左边的部分
  17.         sum += query(leftnode, start, mid, l, r);
  18.     else //否则
  19.         sum += query(rightnode, mid + 1, end, l, r);
  21.     return sum;
  22. }

题目

01

有 2^n(n\le7)2n(n≤7) 个国家参加世界杯决赛圈且进入淘汰赛环节。我经知道各个国家的能力值，且都不相等。能力值高的国家和能力值低的国家踢比赛时高者获胜。1 号国家和 2 号国家踢一场比赛，胜者晋级。3 号国家和 4 号国家也踢一场，胜者晋级……晋级后的国家用相同的方法继续完成赛程，直到决出冠军。给出各个国家的能力值，请问亚军是哪个国家？ 输入输出样例： 输入 3 4 2 3 1 10 5 9 7 输出： 1 —-洛谷 | P4715 【深基16.例1】淘汰赛

分析题目可知，我们可以用一个线段树—根节点装的是两个子节点的最大值，冠军肯定是 tree[2] 和 tree[3]中的一个，亚军就是其中较小的一个

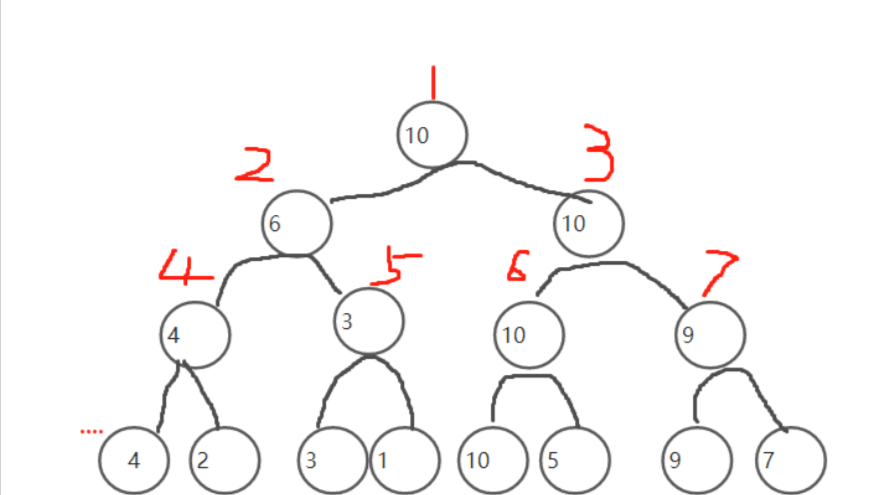image.png红色为 线段树数组编号

  1. #include <iostream>
  2. #include <cstring>
  3. #include <algorithm>
  4. using namespace std;
  5. #define ll long long
  6. const int N = 155;
  8. struct Team{
  9.     int id,ability;//队伍序号和能力值
  10. };
  11. Team maxt(Team a, Team b){
  12.     return a.ability > b.ability? a:b;
  13. }
  14. Team mint(Team a, Team b){
  15.     return a.ability < b.ability? a:b;
  16. }
  18. Team a[N],tree[4*N];
  19. void build(int node, int start, int end){
  20.     if(start == end){
  21.         tree[node] = a[start];
  22.         return;
  23.     }
  25.     int ln = node * 2, rn = node * 2 + 1;
  26.     int mid = (start + end) / 2;
  27.     build(ln, start, mid);
  28.     build(rn, mid + 1, end);
  29.     tree[node] = maxt(tree[ln], tree[rn]);
  30. }
  31. int main(){
  32.     int n;cin>>n;
  33.     for(int i = 1; i <= (1<<n); ++i){
  34.         cin>>a[i].ability;
  35.         a[i].id = i;
  36.     }
  37.     build(1,1,(1<<n));
  38.     cout<<mint(tree[2],tree[3]).id;
  39.     return 0;
  40. }

相信你看了上面的内容，看这个应该没有问题。

总结

如有疏漏，欢迎指正。