探索 前序=》后序

L2-004 这是二叉搜索树吗？ (25 分)|二叉搜索树性质：前序遍历->后序遍历

假设它是二叉搜索树，一开始isMirror为FALSE，根据二叉搜索树的性质将已知的前序转换为后序，转换过程中，如果发现最后输出的后序数组长度不为n，那就设isMirror为true，然后清空后序数组，重新再转换一次（根据镜面二叉搜索树的性质），如果依旧转换后数组大小不等于n，就输出NO否则输出YES 原文链接：https://blog.csdn.net/liuchuo/article/details/52160484

#include <bits/stdc++.h>
using namespace std;
#define ll long long
typedef pair<int, int> PII;
#define FOR(i, n, m) for (int i = n; i < m; ++i)
int n, pre[1005];
vector<int> resv;
bool is_mir = 0;
void solve(int root, int tail) {
  if (root > tail) return;
  int i = root + 1, j = tail;  // 用双指针是因为不能确定他是二叉搜索树，单指针可能误判
  if (!is_mir) {
    while (i <= tail && pre[i] < pre[root]) i++;  //找该节点的左子树
    while (j > root && pre[j] >= pre[root]) j--;  //找该节点的右子树
  } else {
    while (i <= tail && pre[i] >= pre[root]) i++;
    while (j > root && pre[j] < pre[root]) j--;
  }
  solve(root + 1, i - 1);
  solve(j + 1, tail);
  resv.push_back(pre[root]);
}
int main() {
  cin >> n;
  FOR(i, 0, n) cin >> pre[i];
  solve(0, n - 1);
  if (resv.size() != n) {
    resv.clear();
    is_mir = 1;
    solve(0, n - 1);
  }
  if (resv.size() != n) {
    cout << "NO" << endl;
  } else {
    cout << "YES" << endl;
    FOR(i, 0, resv.size()) {
      if (i != 0) cout << " ";
      cout << resv[i];
    }
  }
  return 0;
}

前序+中序=>后序

因为前序（根左右）最先出现的总是根结点，所以令root为前序中当前的根结点下标（并且同时把一棵树分为左子树和右子树）。start为当前需要打印的子树在中序中的最左边的下标，end为当前需要打印的子树在中序中最右边的下标。递归打印这棵树的后序，递归出口为start > end。i为root所表示的值在中序中的下标，所以i即是分隔中序中对应root结点的左子树和右子树的下标。
先打印左子树，后打印右子树，最后输出当前根结点pre[root]的值。 https://www.liuchuo.net/archives/2087

#include <cstdio>
using namespace std;
int pre[] = {1, 2, 3, 4, 5, 6};
int in[] = {3, 2, 4, 1, 6, 5};
void post(int root, int start, int end) {
    if(start > end) 
        return ;
    int i = start;
    while(i < end && in[i] != pre[root]) i++;
    post(root + 1, start, i - 1);
    post(root + 1 + i - start, i + 1, end);
    printf("%d ", pre[root]);
}
int main() {
    post(0, 0, 5);
    return 0;
}

i-start 其实就是 leftSize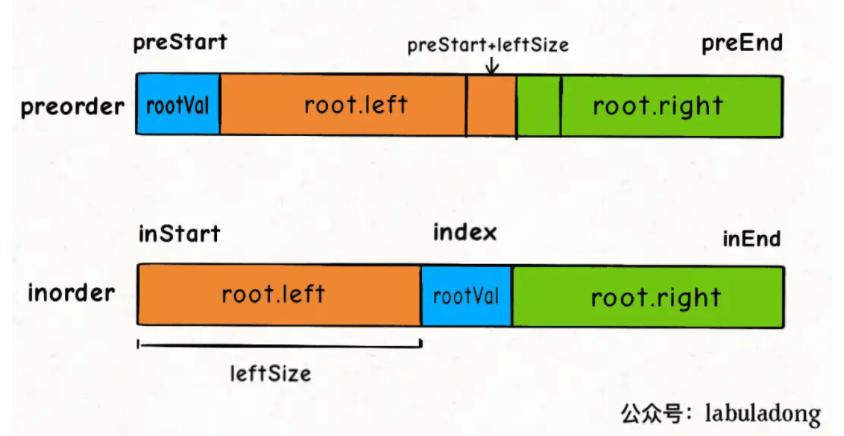
图片来自公众号labuladong

前序+中序=>层序

L2-011 玩转二叉树 (25 分)

关于镜面反转一棵树，只需要在记录 下标时，左孩子为2 index + 2， 右孩子为2 index + 1，在递归完成后level数组中非-1的数就是按照下标排列的层序遍历的顺序

#include<bits/stdc++.h>
using namespace std;
vector<int> pre, in, level(10000,-1);
void levelorder(int root, int start, int end, int index){
    if(start>end)return;
    int i =start;
    while(i<end && in[i] != pre[root])i++;
    level[index] = pre[root];
    levelorder(root + 1, start, i - 1, 2 * index + 2);
    levelorder(root + 1 + i - start, i + 1, end, 2 * index + 1 );
}
int main()
{
    ios::sync_with_stdio(false);
    int n, cnt = 0;
    cin>>n;
    in.resize(n);
    pre.resize(n);
    for(int i = 0;i<n;i++)cin>>in[i];
    for(int i = 0; i<n;i++)cin>>pre[i];
    levelorder(0,0,n-1,0);
    for(int i =0;i<level.size();i++){
        if(level[i] != -1 && cnt != n-1){
            cout<<level[i]<<" ";
            cnt++;
        }else if(level[i] != -1){
            cout<<level[i];
            break;
        }
    }
    return 0;
}

后序+中序=>层序

L2-006 树的遍历 (25 分)

层序遍历利用 map 的有序性来完成。
传入左孩子、右孩子下标即可。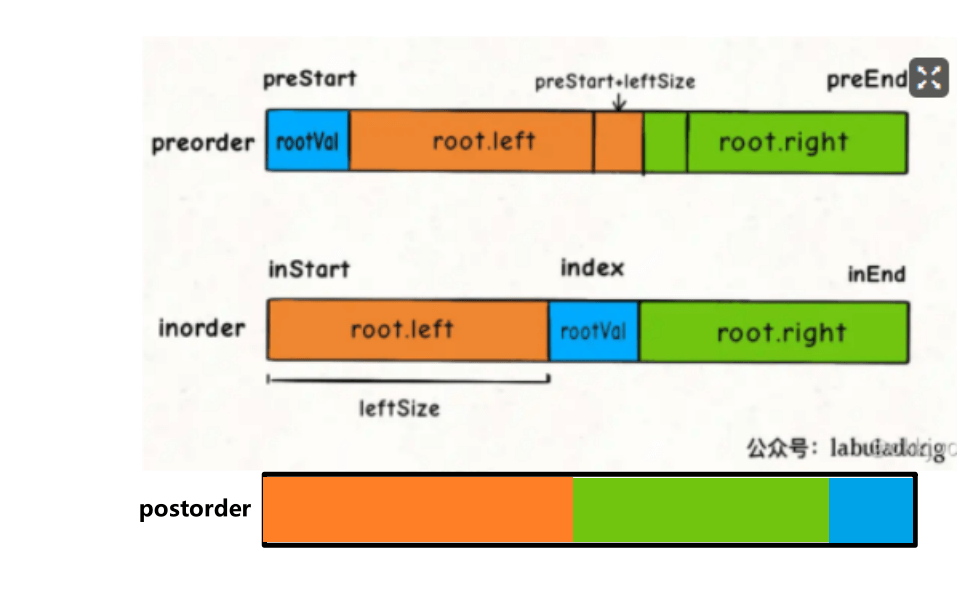

#include<bits/stdc++.h>
using namespace std;
vector<int> post,in;
map<int,int> level;
void pre(int root, int start, int end, int index){
    if(start > end)return;
    int i=start;
    while(i<end && in[i] != post[root])i++;//此时 end - i 就是rightSize
    level[index] = post[root];
    pre(root-1-end+i, start, i-1, 2*index+1);
    pre(root-1, i+1, end, 2*index+2);
}
int main()
{
    ios::sync_with_stdio(false);
    int n;cin>>n;
    post.resize(n);
    in.resize(n);
    for(int i =0;i<n;i++)cin>>post[i];
    for(int i =0;i<n;i++)cin>>in[i];
    pre(n-1,0,n-1,0);
    auto it = level.begin();
    cout<<it->second;
    while(++it!=level.end())printf(" %d",it->second);
    return 0;
}

完全二叉树+后序=> 层序遍历

L2-035 完全二叉树的层序遍历 (25 分)

https://pintia.cn/problem-sets/994805046380707840/problems/1336215880692482058
在 post中保存输入的后序遍历序列，在sequ保存从根节点开始按层序遍历序列的序号。深度优先搜索index标表示当前节点，大于n则返回。按照完全二叉树的遍历原理进行后序遍历，先进入左右子树（编号为index2 和 index2+1，即index右移1位，和index右移1位+1），cnt为后序遍历的位置标记，并将当前所在的后序遍历的元素，填入sequ[index]内

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define FOR(i,n,m) for(int i =n;i<m;++i)
int n,cnt,post[32],sequ[32];
void dfs(int index){
    if(index > n)return;
    //左右中
    dfs(index<<1);//左节点 index*2
    dfs(index<<1 | 1);//右节点 index*2+1
    sequ[index]=post[cnt++];
}
int main()
{
    ios::sync_with_stdio(false);
    cin>>n;
    FOR(i,0,n)cin>>post[i];
    dfs(1);//根节点的下标
    cout<<sequ[1];
    FOR(i,2,n+1)cout<<" "<<sequ[i];
    return 0;
}