时间复杂度均为 [log(n)] ： 单点修改：更改数组中一个元素的值 区间查询：查询一个区间内所有元素的和

    注意到对 [a,b]进行区间查询只需查询[0,a]和 [0, b]然后相减即可（前缀和就是这样进行区间查询的），所以我们可以把区间查询问题转化为求前n项和的问题。

    关于数组的维护，有个很自然的想法：可以用一个数组 树状数组 - 图1 维护若干个小区间，单点修改时，只更新包含这一元素的区间；求前n项和时，通过将区间进行组合，得到从1到n的区间，然后对所有用到的区间求和。

    树状数组就是这样一种结构，它巧妙地利用了二进制（实际上，树状数组的英文名BIT，直译过来就是二进制下标树）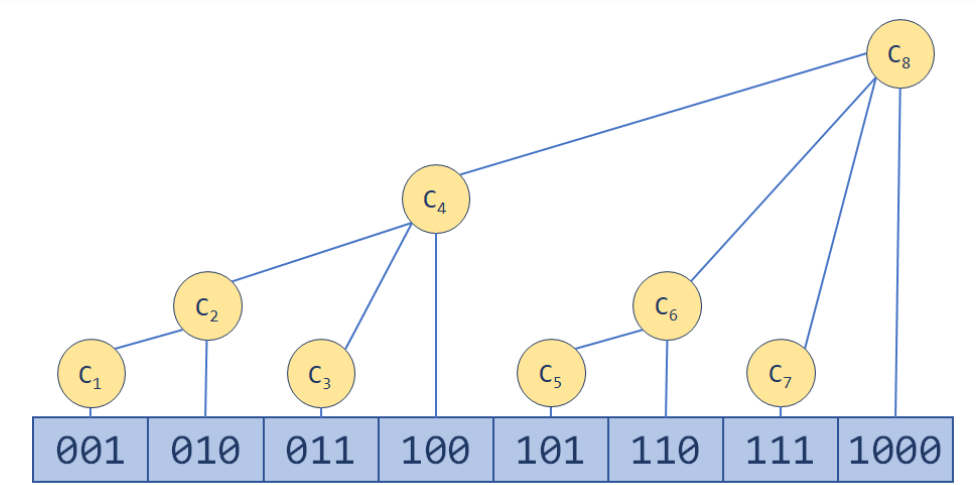
    image.png

    例如11，转化为二进制数就是 树状数组 - 图3 ，如果我们要求前11项和，可以分别查询 树状数组 - 图4 、树状数组 - 图5以及树状数组 - 图6的和再相加。这三个区间怎么来的呢？其实就是不断地去掉二进制数最右边的一个1的过程

    我们定义，二进制数最右边的一个1，连带着它之后的0为 [公式]

    lowbit(x)=x&-x

    计算机里有符号数一般是以补码的形式存储的。-x相当于x按位取反再加1，会把结尾处原来1000…的形式，变成0111…，再变成1000…；而前面每一位都与原来相反。这时我们再把它和x按位与，得到的结果便是lowbit(x)。

    1. #define lowbit(x) ((x) & (-x))
    2. //更新一个点
    3. inline void update(int i, int x)
    4. {
    5.     for (int pos = i; pos < MAXN; pos += lowbit(pos))
    6.         tree[pos] += x;
    7. }
    9. //查询[0,n]
    10. inline int query(int n)
    11. {
    12.     int ans = 0;
    13.     for (int pos = n; pos; pos -= lowbit(pos))
    14.         ans += tree[pos];
    15.     return ans;
    16. }
    18. //查询[a,b]
    19. inline int query(int a, int b)
    20. {
    21.     return query(b) - query(a - 1);
    22. }