存图-链式前向星

可以说该方法的前身是 邻接矩阵和邻接表，但是都有一些差强人意，于是就有大佬研究出了这么个数据结构，我觉得可以理解为 数组模拟链表

[

](https://pintia.cn/problem-sets/994805046380707840/problems/1386335159927652361)

主要结构：

struct E
{
    int to,w,next;
}Edge[maxn];
int tot,Head[maxn];

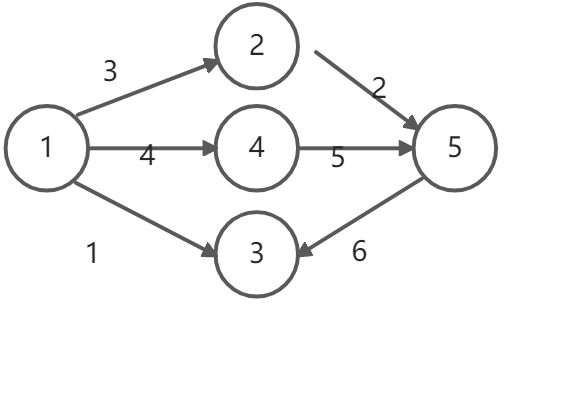
邻接表 :

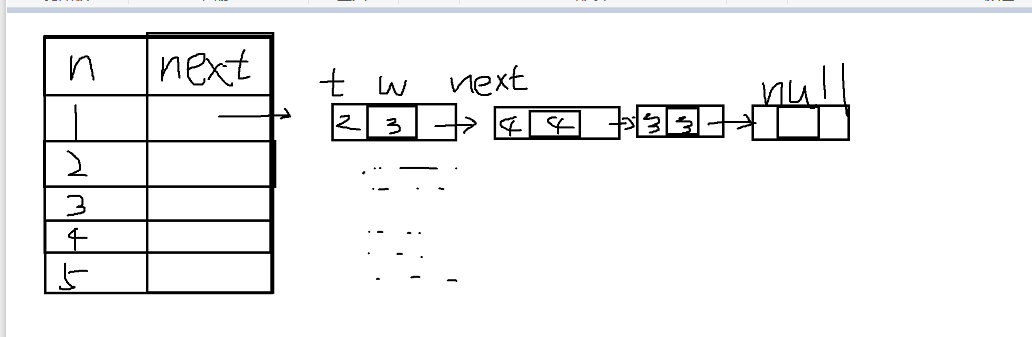
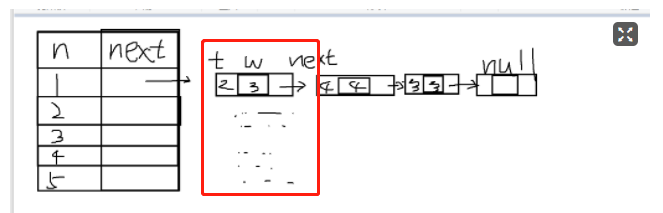
head就是这一块

初始化

int main(){
    //初始化
    memset(Head,-1,sizeof Head);
}

有人习惯用 -1 作为空的标志，有人习惯用 0 ，这里我使用 -1

遍历点的边

遍历从 u 出发能够”一步”到达的点或者说是 边

void traversal(int u){
    //遍历从 u 出发能够"一步"到达的点或者说是 边
    for(int i  = Head[u];~i;i=Edge[i].next){
        int v = Edge[i].to,w=Edge[i].w;
        //do something
    }
}

新添加一条新的边

void addEdge(int u,int v,int w){
    //第 tot 条边的u->v，长度为 w
    Edge[tot].to = v;
    Edge[tot].w = w;
    //让之前 u 作为起点的最新添加的一条边 作为 第 tot 条边的下一条边，使其序号记为第 tot 条边的 next
    Edge[tot].next = Head[u];
    //更新，现在 u 作为起点的 最新添加的一条边 的序号 更新为 tot；tot++，为下一次添加边做准备 
    Head[u] = tot++;
}

head[1] 就是 1 这个点后面的 最新添加的一条边的序号，插入一条新边时可以理解为 头插法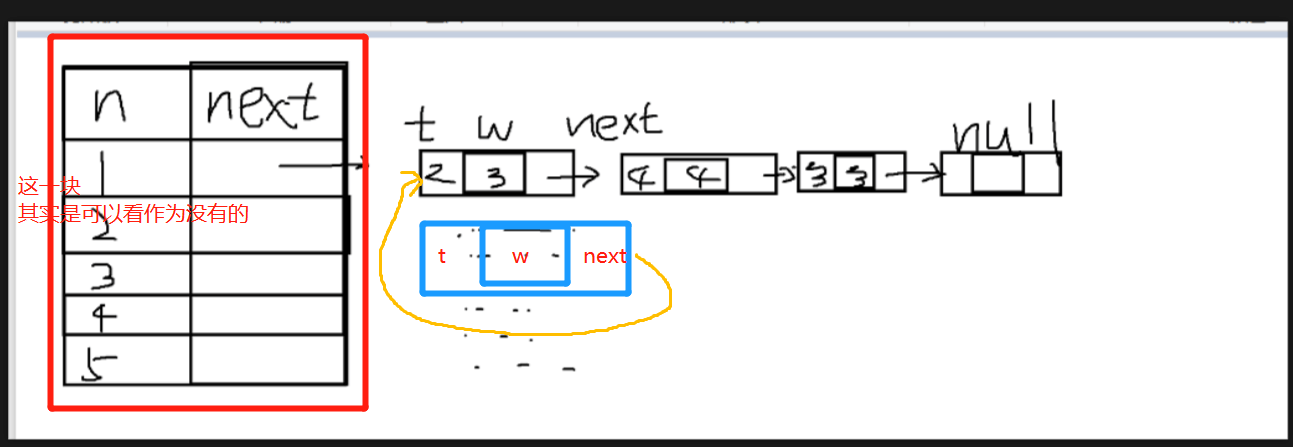

注意：

• 红色部分其实是不存在的的，只有边的序号（tot）、点的 head 、边的 next，使各条边联系在一起
• tot ：边的序号，全局的，每次新增一条边之后都有 tot++ ，为新增下一条新边做准备。

总结

链式前向星其实就是一个 简化版的 好写一些的 易用的 邻接表

题目

L2-038病毒溯源 ：存图 | dfs

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const  int N = 10010,M = 10010;
int n;
 //结构体拆为三个数组了，因为没有权，也就没有w
int h[N],    // 对于每个点k，开一个单链表，存储所有k可以走到的点。h[k]存储这个单链表的头结点
    e[M],     //e[idx] : 第idx条边的终点
    ne[M],    //ne[idx] : 以第idx边的起点作为起点 的 下一条边
    idx=0;
int son[N];//每个点的儿子
bool st[N];
void add(int a,int b){
    e[idx] = b,ne[idx] = h[a],h[a] = idx++;
}
int dfs(int u){
    int res = 0;//当前往下走的最长路径
    son[u] = -1; 
    for(int  i = h[u];i!= -1;i = ne[i]){
        int j = e[i];
        int d = dfs(j);
        if(res < d) res = d,son[u] = j;
        else if(res == d) son[u] = min(son[u],j);
    }
    return res + 1;
}
int main(){
    memset(h,-1,sizeof(h));//设置邻接表的表头
    scanf("%d",&n);
    for(int i = 0; i < n; i++){
        int cnt;
        scanf("%d",&cnt);
        while(cnt--){
            int x;
            scanf("%d",&x);
            add(i,x);//连接一条从i到x的边
            st[x] = true;//x有父节点
        }
    }
    int root = 0;
    while(st[root]) root++;//找父节点
    printf("%d\n",dfs(root));
    printf("%d",root);
    while(son[root] != -1){
        root = son[root];
        printf(" %d",root);
    }
    return 0;
}