1、首先，我们要记录下目前已知的回文串能够覆盖到的最右边的地方
2、同时，覆盖到最右边的回文串所对应的回文中心也要记录
3、以每一位为中心的回文串的长度也要记录，后面进行推断的时候能用到
4、对于新的中心，我们判断它是否在右边界内，若在，就计算它相对右边界回文中心的对称位置，从而得到一些信息，同时，如果该中心需要进行扩展，则继续扩展就行。

1、先对字符串进行预处理，两个字符之间加上特殊符号#
2、然后遍历整个字符串，用一个数组来记录以该字符为中心的回文长度，为了方便计算右边界，我在数组中记录长度的一半（向下取整）
3、每一次遍历的时候，如果该字符在已知回文串最右边界的覆盖下，那么就计算其相对最右边界回文串中心对称的位置，得出已知回文串的长度
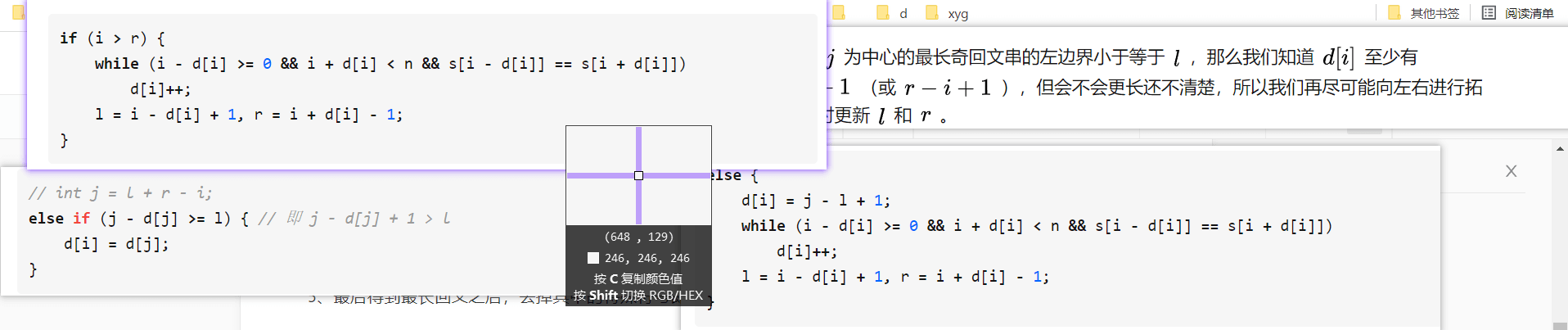
4、判断该长度和右边界，如果达到了右边界，那么需要进行中心扩展探索。当然，如果第3步该字符没有在最右边界的“羽翼”下，则直接进行中心扩展探索。进行中心扩展探索的时候，同时又更新右边界
5、最后得到最长回文之后，去掉其中的特殊符号即可

• https://zhuanlan.zhihu.com/p/404216115
• https://mp.weixin.qq.com/s?__

string expandS(string s){
       string Str = "*#";
       for(int i = 0;i<s.size();i++){
           Str += s[i];
           Str += '#';
       }
       return Str;
   }

for (int i = 0, l = 0, r = -1; i < n; ++i) {
    int j = l + r - i;
    d[i] = max(min(d[j], j - l + 1), 0);
    if (j - d[j] < l) {
        while (i - d[i] >= 0 && i + d[i] < n && s[i - d[i]] == s[i + d[i]])
            d[i]++;
        l = i - d[i] + 1, r = i + d[i] - 1;
    }
}

string expandS(string s){
   string Str = "*#";
   for(int i = 0;i<s.size();i++){
       Str += s[i];
       Str += '#';
   }
   return Str;
}
string Manacher(string s){
   string s1 = expandS(s);
   int idd=0,maxx=0,Len[10000],maxLen=0,start=0;//idd 目前最大的Len对应的下标，Len[idd]+i=maxx
   for(int i =0;i<s1.length();i++){
       if(i<maxx)Len[i]=min(Len[2*idd-i],maxx-i);
       else Len[i] = 1;//i在max右边，则直接暴力求解
       while(s1[i+Len[i]]==s1[i-Len[i]] && i+Len[i]<s1.size() && i-Len[i]>0){Len[i]++;}//暴力
       if(Len[i]+i > maxx){//更新 maxx 和 idd的值               
           maxx = Len[i] + i;
           idd = i;
       }
       if(Len[i]-1 > maxLen){
           maxLen = Len[i]-1;//Len[i]-1 为原来字符串的回文最大长度
           start = (idd-maxLen)/2;//原来字符串的回文起始位置（idd先变回原字符串位置，再减去长度一般即可）
       }
   }
   return s.substr(start,maxLen);
}

例题

L2-008 最长对称子串 (25 分)

#include<bits/stdc++.h>
using namespace std;
string expendS(string s){
    string _s = "*#";
    for(int i =0;i<s.size();i++){
        _s += s[i];
        _s += '#';
    }
    return _s;
}
string Manacher(string s){
    string _s =expendS(s);
    int idd = 0,//目前最大的Len对应的下标
        maxx=0,Len[100000],//maxx = Len[idd]+idd
        maxLen=0,//原始字符串s中的回文最大长度
        start=0;//原始字符串s中的最长回文的起始位置
    for(int i =0;i<_s.size();i++){
        if(i<maxx)Len[i]=min(Len[2*idd-i],maxx-i);
        else Len[i]=1;//i在maxx右边，无法利用前面的规律，则直接暴力
        //无论如何，都要再看看有没有新的边界chuxian
        while(i+Len[i] < _s.size() && i-Len[i] > 0 && 
             _s[i+Len[i]]==_s[i-Len[i]])Len[i]++;
        //是否要更新
        if(Len[i]+i > maxx){
            maxx = Len[i]+i;
            idd = i;
        }
        //Len[i]-1 就是在原来字符串s中的回文最大长度
        if(Len[i]-1 > maxLen){
            maxLen = Len[i]-1;
            start = (idd-maxLen)/2;
        }
    }
    return s.substr(start,maxLen);
}
int main()
{
    ios::sync_with_stdio(false);
    string s;
    getline(cin,s);
    cout<<Manacher(s).size();
    return 0;
}