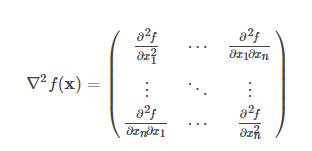上面我们谈论到了，如果像要求得的最大化，就要求得的最小化，而约束的条件是：

你可能认为，这只有一个约束条件，事实上，这个约束条件有n个，因为这是一个n维数据。
在解决这样一个复杂的问题之前，让我们从一个简单的问题开始，我们将首先研究如何解决无约束的最优化问题，更具体而言，我们要研究无约束的最小化。这就是寻找输入使函数返回最小值的问题。（注意：在SVM情况下，我们希望最小化的范数,我们可以称之为f并且把它写为）

无约束最小化

我们首先指定一个点,这个点是一个特殊点，并不是任意点。我们怎么知道这个点是不是我们函数的局部最小值，很简单，我们只需要把它带入下面的理论：

理论

假设在是一个二次可微的函数。如果在处满足：一阶导数为0，二阶导数>0，那么在这个点就是局部最小值。这是一元函数的情况，如果是多元函数，就要用到黑塞矩阵来判断。

详细理论

如果满足两个条件：

• 一阶导数或者一阶偏导为0

例如：

• 如果黑塞矩阵为正定矩阵时，为极小值。

我们使用简单的方式进行计算：

例子

找到的最小值

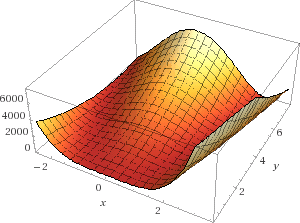
首先，我们要找到梯度等于0的点

所以我们计算出其偏导数然后我们发现

令偏导为0

打开括号

求得：

黑塞矩阵：


计算黑塞矩阵

其行列式为

是一个正定矩阵，所以是其最小值点。

全局最小与局部最小

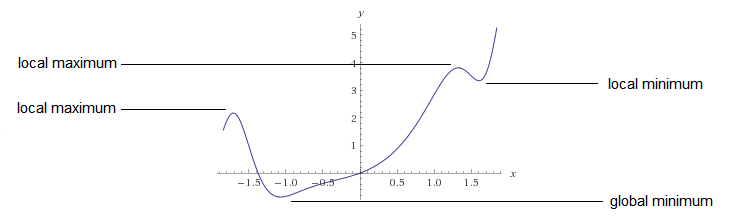
有时候满足上述条件的点有多个，这个时候找出所有的点，找出其中最小的点即为全局最小(global minimum)。