用到了Adaboost来提升弱分类器成为强分类器，所以找一下相关的知识，主要是找到相关的例子和介绍。

一、AdaBoost简介

  Boosting, 也称为增强学习或提升法，是一种重要的集成学习技术， 能够将预测精度仅比随机猜度略高的弱学习器增强为预测精度高的强学习器，这在直接构造强学习器非常困难的情况下，为学习算法的设计提供了一种有效的新思路和新方法。其中最为成功应用的是，Yoav Freund和Robert Schapire在1995年提出的AdaBoost算法。<br />      AdaBoost是英文"Adaptive Boosting"（自适应增强）的缩写，它的自适应在于：前一个基本分类器被错误分类的样本的权值会增大，而正确分类的样本的权值会减小，并再次用来训练下一个基本分类器。同时，在每一轮迭代中，加入一个新的弱分类器，直到达到某个预定的足够小的错误率或达到预先指定的最大迭代次数才确定最终的强分类器。

二、基本原理

Adaboost算法基本原理就是将多个弱分类器（弱分类器一般选用单层决策树）进行合理的结合，使其成为一个强分类器。
Adaboost采用迭代的思想，每次迭代只训练一个弱分类器，训练好的弱分类器将参与下一次迭代的使用。也就是说，在第N次迭代中，一共就有N个弱分类器，其中N-1个是以前训练好的，其各种参数都不再改变，本次训练第N个分类器。其中弱分类器的关系是第N个弱分类器更可能分对前N-1个弱分类器没分对的数据，最终分类输出要看这N个分类器的综合效果。

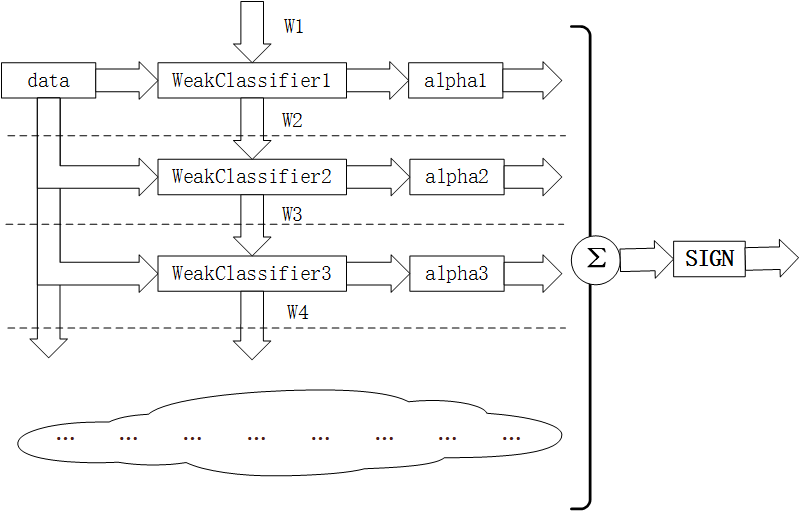
图1. 训练原理图

三、Adaboost实例

3.1 数据

这里使用的是决策树桩作为弱分类器，使用GeGebra画图比较方便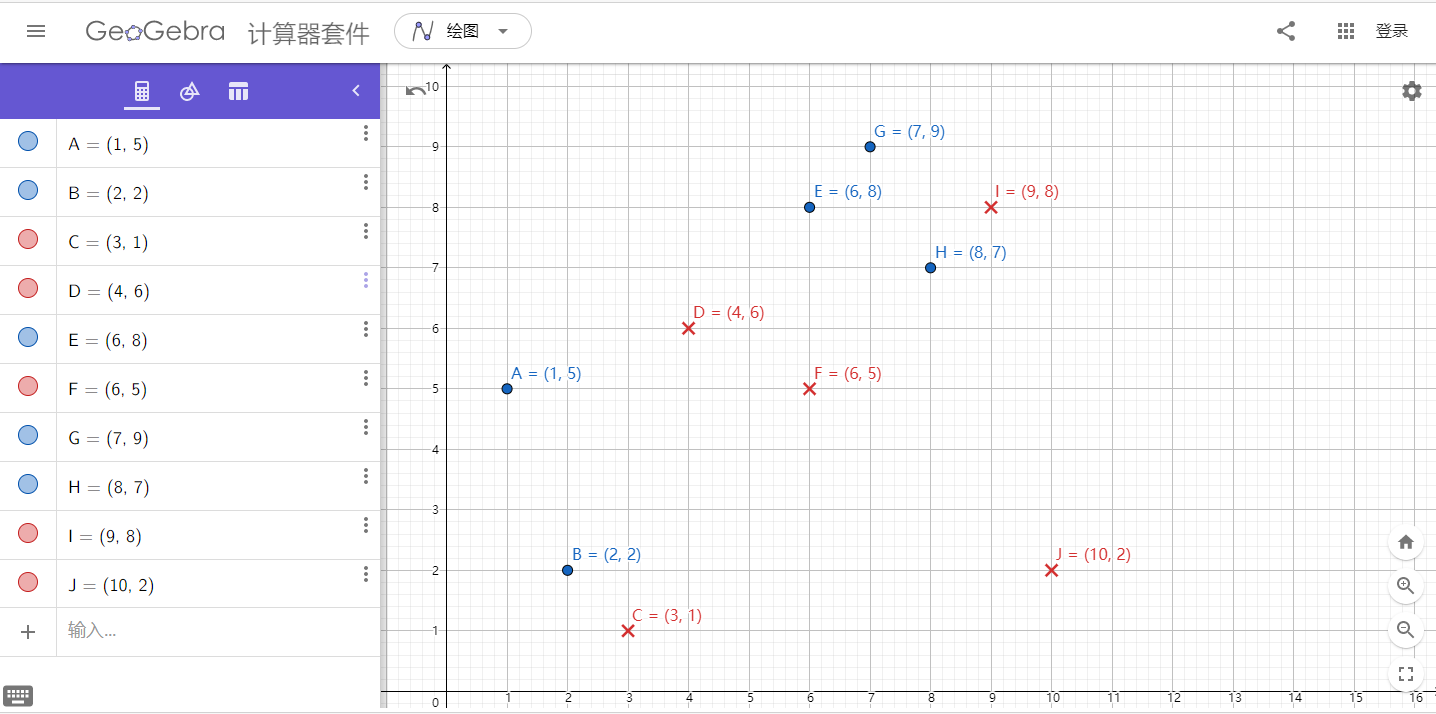

图2. 数据分布

3.2 分类器

将这10个样本作为训练数据，根据 X 和Y 的对应关系，可把这10个数据分为两类，图中用蓝⚪表示类别1，用红❌表示类别-1。本例使用水平或者垂直的直线作为分类器，下图中已经给出了三个弱分类器，即：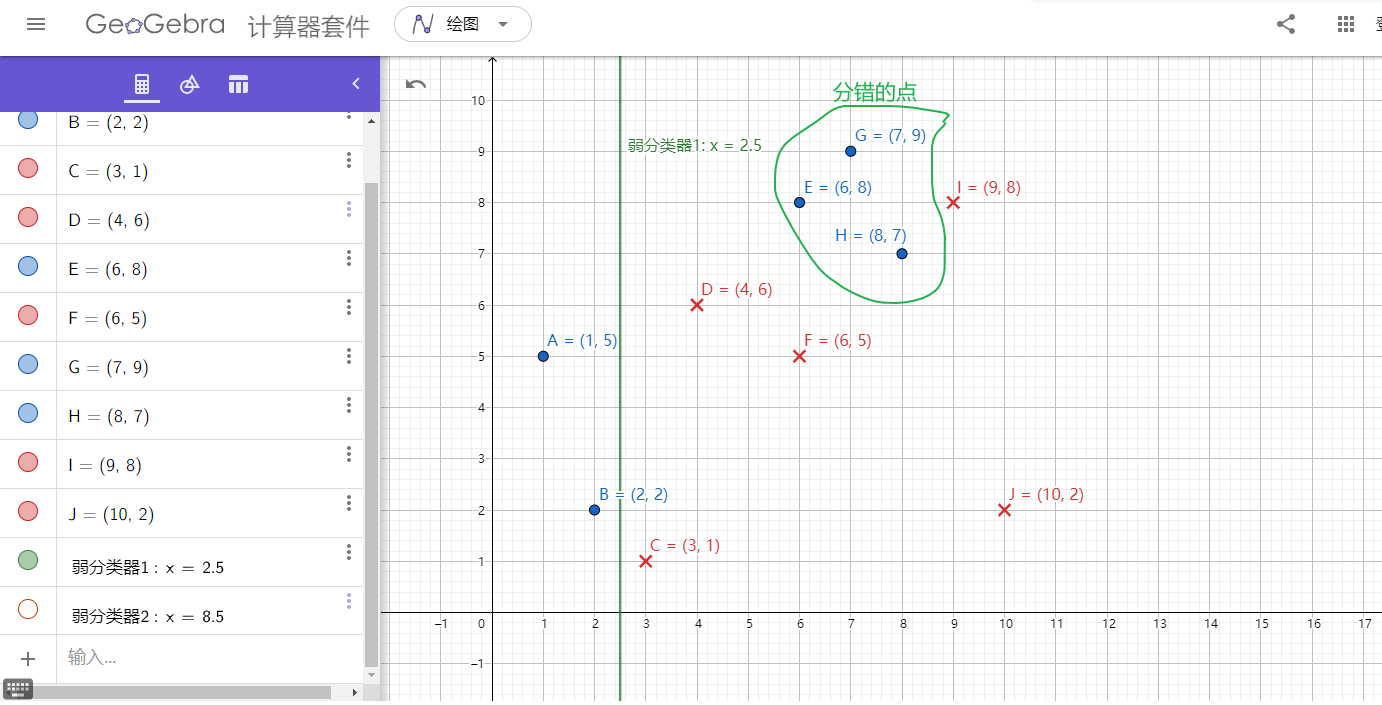


图3. 弱分类器1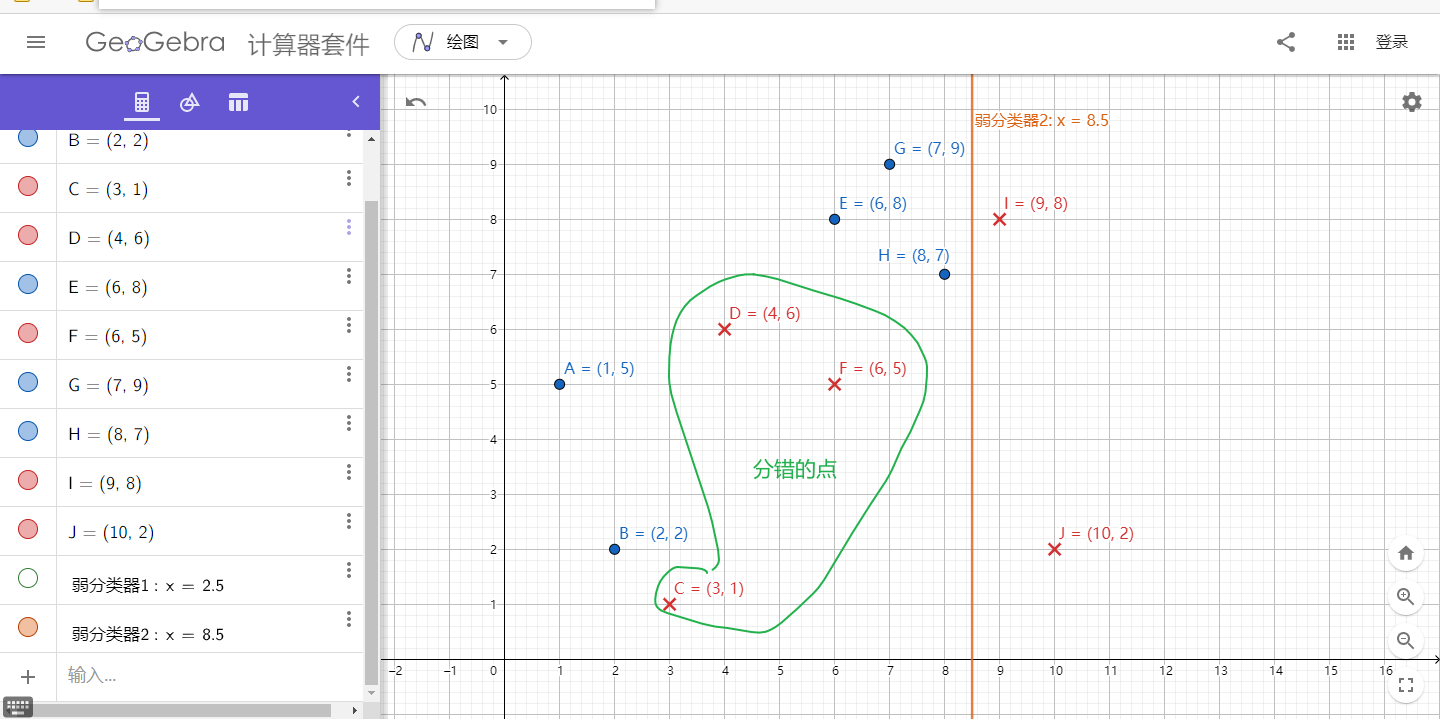


图2. 弱分类器2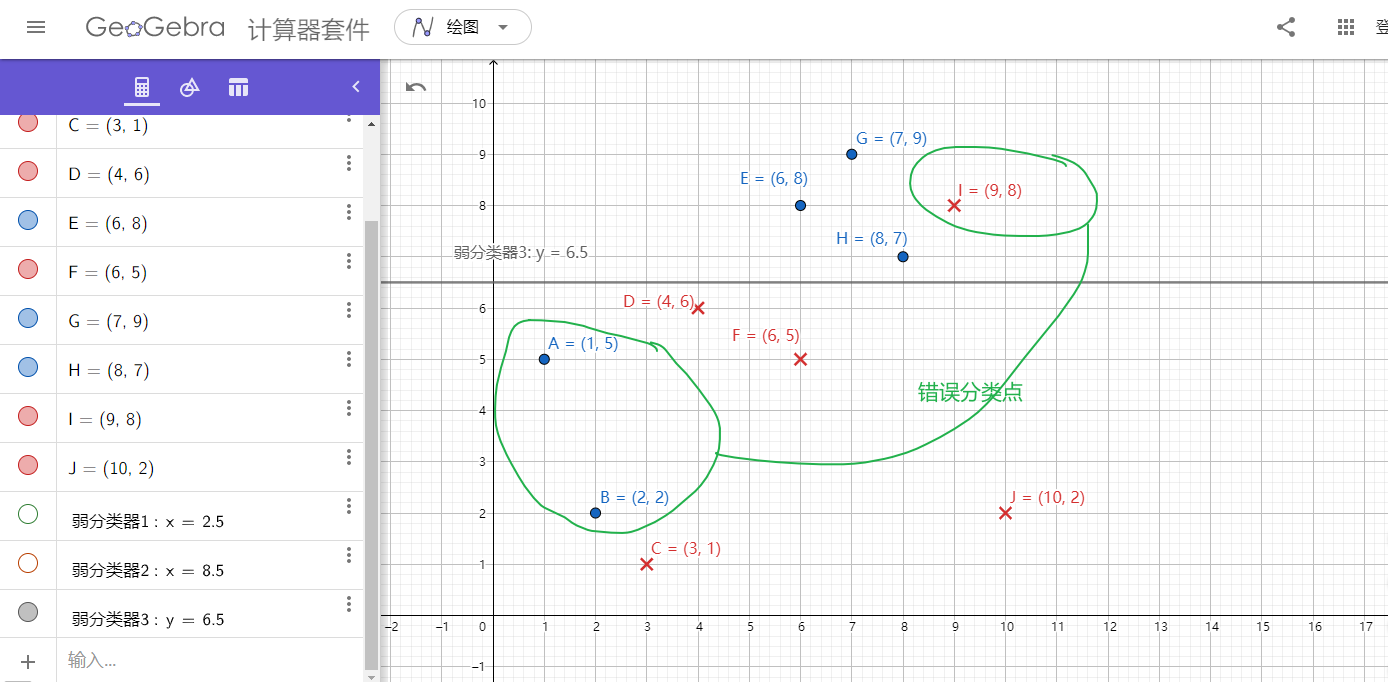


图3. 弱分类器3

3.3 初始化：

首先需要初始化训练样本数据的权值分布，每一个训练样本最开始时都被赋予相同的权值：，这样训练样本集的初始权值分布：
令每个权值，其中，，然后分别对于等值进行迭代（表示迭代次数，表示第轮），下表已经给出训练样本的权值分布情况：

表1. 初始权值分布

3.4 第一次迭代

第1次迭代t=1：
初试的权值分布为（10个数据，每个数据的权值皆初始化为0.1），

在权值分布的情况下，取已知的三个弱分类器和中误差率最小的分类器作为第1个基本分类器（三个弱分类器的误差率都是0.3，那就取第1个吧）.
在分类器情况下，样本点被错分，因此基本分类器的误差率为：

根据误差率计算的权重：

然后，更新训练样本数据的权值分布，用于下一轮迭代，对于正确分类的训练样本（共7个）的权值更新为：

对于错误分类的样本的权值更新为：

这样，第1轮迭代后，最后得到各个样本数据新的权值分布：

由于样本数据“5 7 8”被H(x)分错了，所以它们的权值由之前的0.1增大到1/6；反之，其它数据皆被分正确，所以它们的权值皆由之前的0.1减小到1/14，下表给出了权值分布的变换情况：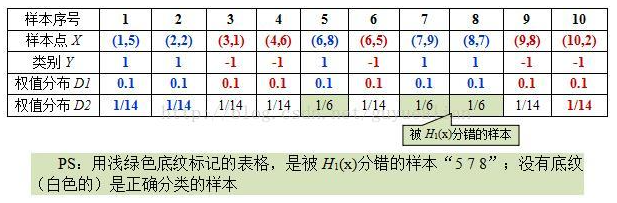

表2. 权值分布变换情况
可得分类函数：。此时，组合一个基本分类器作为强分类器在训练数据集上有3个误分类点（即），此时强分类器的训练错误为：0.3

3.5 第二次迭代

在权值分布的情况下，再取三个弱分类器和中误差率最小的分类器作为第2个基本分类器：

①　当取弱分类器h=X=2.5时，此时被错分的样本点为“5 7 8”： ②　当取弱分类器h=X=8.5时，此时被错分的样本点为“3 4 6”： ③　当取弱分类器h=X=6.5时，此时被错分的样本点为“1 2 9”： 因此，取当前最小的分类器h作为第2个基本分类器H(x)：

把样本3,4,6分错了，根据可知它们的权值为,所以在训练数据集上的误差率：

根据误差率计算的权重：

更新训练后样本数据的权值分布，对于正确分类的样本权值更新为：

对于错误分类的权值更新为：

这样，第2轮迭代后，最后得到各个样本数据新的权值分布：

下表给出了权值分布的变换情况：

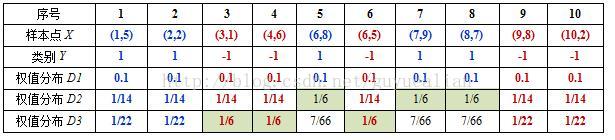
表3. 权值更新情况
可得分类函数：。此时，组合两个基本分类器作为强分类器在训练数据集上有3个误分类点（即），此时强分类器的训练错误为：0.3

3.6 第三次迭代

在权值分布D的情况下，再取三个弱分类器h、h和h中误差率最小的分类器作为第3个基本分类器H(x)：

①　当取弱分类器h=X=2.5时，此时被错分的样本点为“5 7 8”： ②　当取弱分类器h=X=8.5时，此时被错分的样本点为“3 4 6”： ③　当取弱分类器h=X=6.5时，此时被错分的样本点为“1 2 9”： 因此，取当前最小的分类器h作为第3个基本分类器H(x)：

把样本1,2,9分错了，根据可知它们的权值为,所以在训练数据集上的误差率：

根据误差率计算的权重：

更新训练后样本数据的权值分布，对于正确分类的样本权值更新为：

对于错误分类的权值更新为：

这样，第2轮迭代后，最后得到各个样本数据新的权值分布：

下表给出了权值分布的变换情况：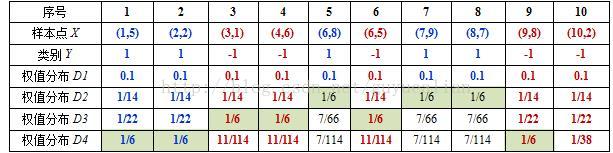

表4. 权值更新情况
可得分类函数：。此时，组合两个基本分类器作为强分类器在训练数据集上有0个误分类点, 至此，整个训练过程结束。整合所有分类器，可得最终的强分类器为：

此时强分类器的训练错误为：0.

四 参考链接

• 参考链接1: https://blog.csdn.net/guyuealian/article/details/70995333
• 参考链接2: 链接过长, 点击进入
• 参考链接3: https://blog.csdn.net/weixin_40118768/article/details/80411482