来源链接

对偶性

在数学优化理论中，对偶性意味着可以从原始问题或者其对偶问题这两个角度来看待优化问题。对偶问题的解决方案为原始问题的解决方案提供了下限。

下限是什么？

比如存在一个数据集合S：。我们可以知道1这个数小于集合S中的所有数，同样地-3这个数也是小于集合S中的所有数。在S中2小于其他数，所以2是S中的下限。但是，2这个下限是所有下限中最大的数，所以我们给它起个名字叫最大下限（infimum）。
同样的情况，也存在上限和最小上限(supremum)。

回到对偶性

既然我们知道下界是什么，对二元性的定义我们了解什么？好吧，这个定义意味着如果您遇到最小化问题，也可以将其视为最大化问题。并且，当您找到此问题的最大值时，它将是最小化问题的解决方案的下限，即，它将始终小于或等于最小化问题的最小值。

我们为什么要关心对偶性

某些情况下，我们将一个问题转换为另一个问题的时候，问题会变得容易思考？例如，下面这个图。我们要求上面函数的最小值=下面函数的最大值。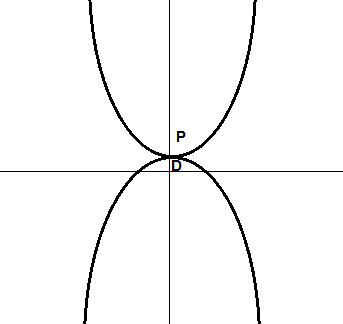

有约束条件的优化问题

一个典型的优化问题，可以写成：

在这个概念当中,f被称作为目标函数(有时也称之为代价函数).我们希望能够通过改变从而找到的最小值.同样也有一个等式函数来作为条件,还有一个不等式函数来作为条件.

遵循这些条件意味着什么

比如你现在需要解决下面的这样一个优化问题:

这个时候没有约束条件,所以我们能够很轻松地找到最小条件就是.如下图所示

等式约束

如果我们添加了一个等式约束条件如下:

我们最后发现满足这个条件的点为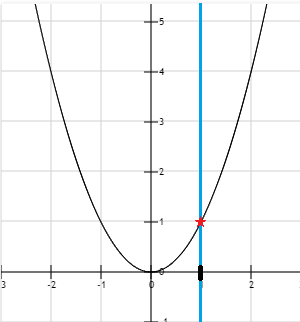

不等式约束

如果这个时候我们想要添加一个等式约束,这个约束如下:

这个时候我们发现,在处为最小值点.

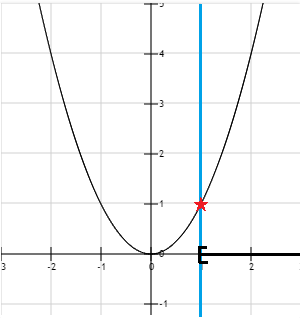
联合条件约束

我们找一个约束条件如下:

我们可以把这样一个式子写成

我们怎么用这样一个约束条件来求解?

在有条件约束的情况下,我们使用拉格朗日极值法来求解函数的极值问题.
需要注意的关键是，拉格朗日乘数的方法仅在等式约束下起作用。因此，我们可以用它来解决一些优化问题：具有一个或多个相等约束的问题。
但是不用担心，拉格朗日乘数也将成为解决不平等约束问题的基础，因此值得理解这种更简单的情况🙂
在解释拉格朗日乘子的概念是什么之前，让我们刷新一下关于轮廓线的记忆。

高等线

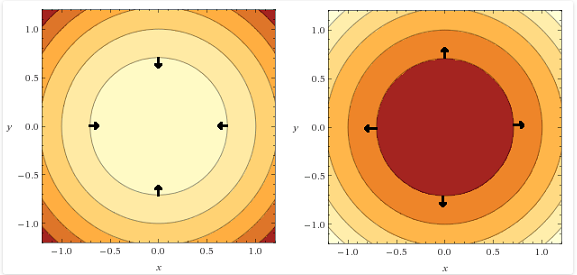
为了更好地理解拉格朗日乘数，理解等高线是很重要的。等高线图是将三维函数可视化为二维函数的一种方法。例如，下图显示了3D显示的函数(左)和等高线图(右)

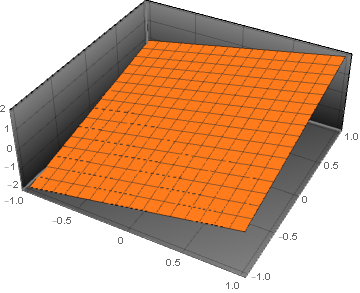
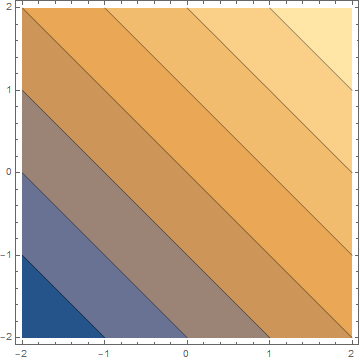
关于等高线的概念

• 对于线上的每一个点,该函数返回相同的值
• 区域越暗,函数的值越小

我们可以在下面的两个图中看到最后一个点,即使他们具有相同的线条,颜色的变化也能够使我们能够在脑海中绘制功能的3D图片.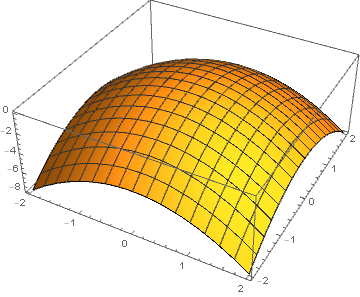


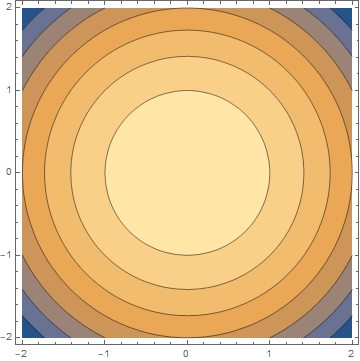
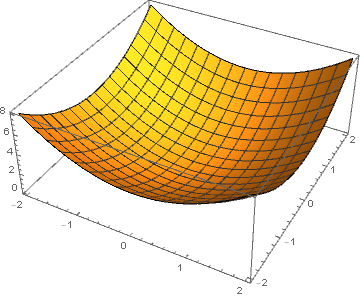
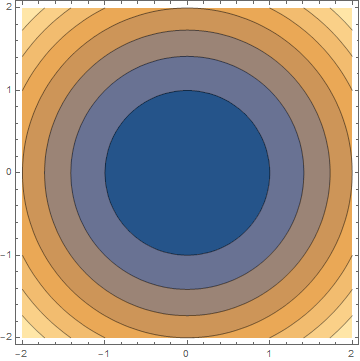
此外,函数的梯度可以视为矢量场,箭头指向函数增加的方向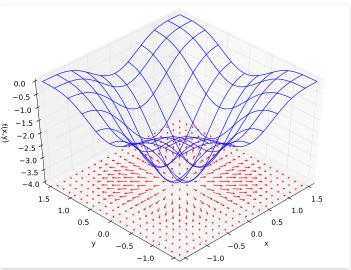

事实证明,我们可以轻松地在高等线上绘制梯度矢量:

• 他们垂直于轮廓线
• 他们应该指出功能正在增加的方向

这是两个等高线图的表示:

回到拉格朗日乘子法

让我们看到下面的优化问题:

我们先看一下这两个函数的等高线图: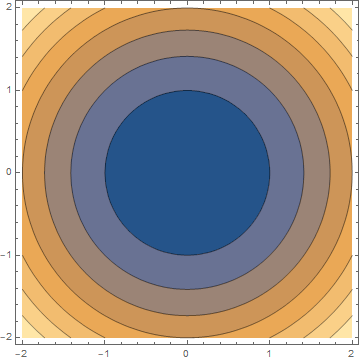

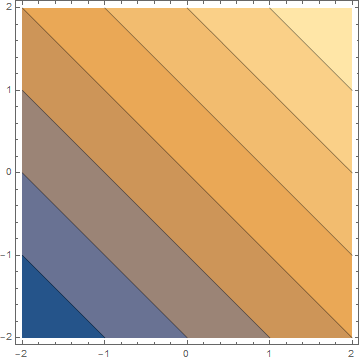
有趣的是，我们可以将两个等高线图组合在一起以可视化这两个函数在一个图上的行为。在下面，您可以看到由蓝线表示的约束函数。
另外，我绘制了目标函数的一些梯度矢量（黑色）和约束函数的一些梯度矢量（白色）。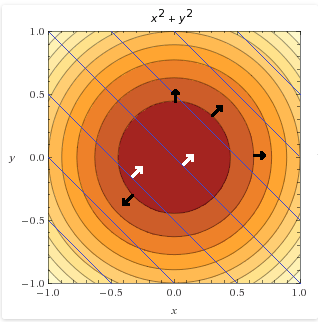

但是，我们对整个约束函数不感兴趣。我们只对满足约束的点感兴趣，即.这意味着我们的点满足上述的g(x,y)条件:

在下面的图中,我们在目标函数的基础上画出了这条线,前面我们也看到了这条线,称之为可行集.

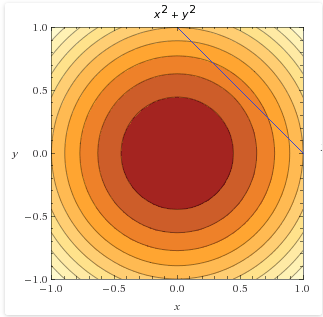
拉格朗日发现了什么?他发现当约束条件和的梯度指向相同的方向的时候,取得了最小值.让我们看看如何找到类似的结论.
在下图中，我们可以看到目标函数和可行集相切的点。我还在黑色中添加了一些目标函数梯度向量，并在白色中添加了一些约束梯度向量。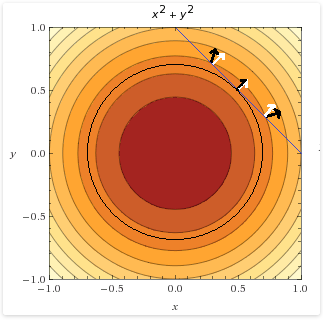

我们可以看到，只有两个向量指向同一方向的点：在约束下，它是目标函数的最小值。
假设您将手指放在图形顶部的第一点(第一个箭头所在点,这点为交点,即满足两个条件的点)上。在这里评估目标函数，发现它返回一些值。现在，您想知道是否有较小的值。您必须停留在蓝线上，否则将违反约束。因此，您可以向左或向右移动。
您想向左走，但是随后您看到目标函数的梯度指向左（记住它总是指向更大的值），所以这可能不是一个好主意。可以肯定的是，您尝试转到左侧。您发现目标函数返回，所以它在增加，这是不行的。这次向右移动，目标函数返回个，很高兴您能朝正确的方向前进。因此，您将像这样继续下去，直到到达两个箭头平行的中心点。但是，当您稍作移动后，您会发现目标函数再次增加。如果不增加目标函数就无法再向右或向左移动，那么可以得出结论，这是最低要求。

这个在数学上是什么意思呢?

拉格朗日告诉我们,要在一个约束条件下找到最小值,我们需要寻找到符合条件(即两个梯度方向相同或相反)的点.
但是是什么,他有是怎么得到的?
这个就是我们说的拉格朗日乘子.因为即使两个函数的梯度在一个方向,但是他们的梯度大小并不相同,这个时候就会有一个标量表示他们的关系.
请注意，此公式不要求梯度具有相同的方向（乘以负数将改变方向），而仅是平行的。这是因为可以同时使用它来查找最大值和最小值（如果要查看方法，请参阅本文的示例1）。

我们怎么样找到满足的点

我们对这个式子做一个简单的变换:

为了让这个事情看起来更加简单,我们定义了一个函数:

我们得到他的梯度为:.这个L函数就叫做拉格朗日函数,我们使用的拉格朗日梯度()意味着这个时候的函数和函数的梯度是平行的.

我们用拉格朗日乘子法来解决这个问题

我们需要解决的问题是:

Step1:我们引入拉格朗日函数:

,它的梯度为:

Step2:我们计算他的梯度问题

我们要解决的问题是:

这就意味着我们要满足下面的式子,即所有的一阶偏导数全部为0:

通过计算上述式子我们得到:
所以我们可以得出结论:在约束条件下,函数的最小值点为,让我们用下面的图做分析来证明它是有效的.

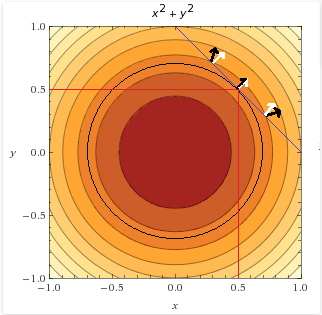
我们可以发现点确实在我们之前的约束条件上,而且它的梯度也满足条件.

结论

在本文中，我们学习了优化中的重要概念：对偶。此外，我们发现优化问题可以具有等式和不等式约束。最终，我们了解了什么是拉格朗日乘数，以及如何使用它们来解决具有一个等式约束的优化问题。
如果您想了解更多有关SVM上下文中的Lagrange乘数的信息，可以阅读这篇非常好的论文，其中展示了如何在更多等式约束和不等式约束下使用它们。

张宇18讲