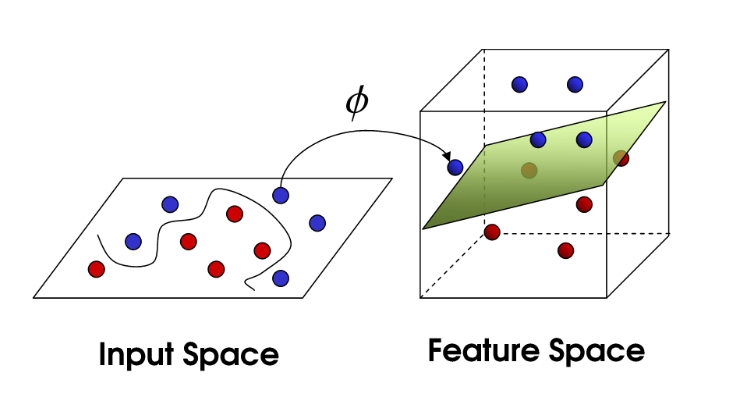
核技巧看起来时统计学和机器学习中最令人迷惑的概念中的一个。它一眼看上去就像是一个真正的数学魔法，更不用提及这个词汇的歧义问题(这个核是不是指评估统计学中的概率密度的一种非参数方式)。向量集合通过T映射关系映射到0向量，即：。
尽管在理解核技巧方面存在一些障碍，但是了解如何在支持向量分类中使用内核非常重要。因为实现支持向量分类器需要指定内核功能，并且尚无确定的通用规则来指导哪种内核最适合我们的特定数据。
从概念上讲，内核技巧还说明了有关数据的不同方式以及机器学习算法查看这些不同的数据表示的一些基本思想。这篇文章主要的介绍如下：

• 在支持向量分类的背景下可视化一些非线性变换
• 介绍了一种思想，即在支持向量分类其中训练核技巧的好处在于唯一的数据表现形式。

  非线性变换

如果数据在原始空间或输入控件中不是线性可分离的，则我们对数据进行变换，将数据从原始空间映射到更高维的特征空间。目标是在转换到高维空间后，这些类可以在这个高维空间中进行线性分离。然后，我们可以拟合决策边界以分离类并进行预测。决策边界将会是这个更高维空间中的超平面。
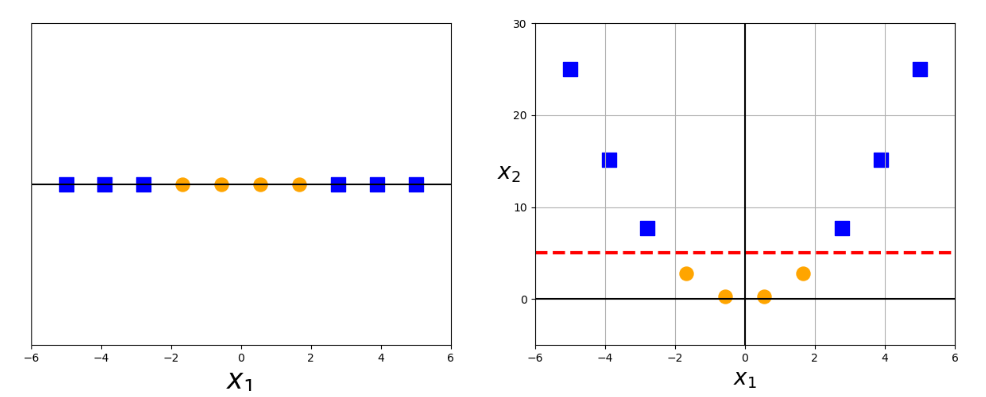
显然很难可视化高维数据，因此我们首先关注应用于一维数据的一些转换。作图显示了我们原始的数据点，很显然，在一维空间中，这个数据是不可分离的，但是在应用了变换就可以将这个一维数据映射到二维空间中，然后这个数据就可以线性分离了。

再看一个例子，我们的数据在二维空间中，很明显是不可分离的，现在我们将其映射到三维空间中。映射关系为：。

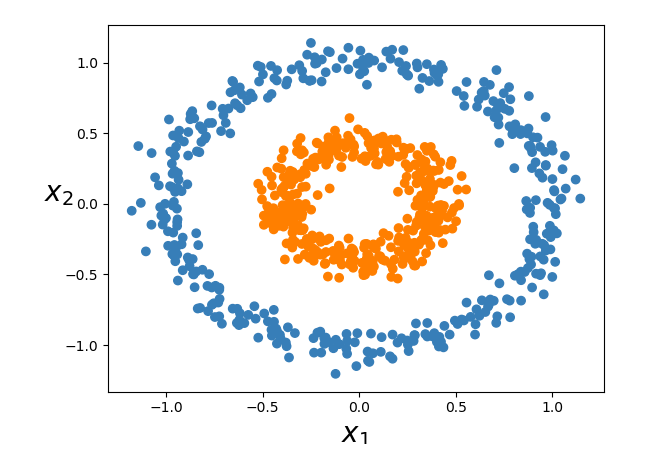
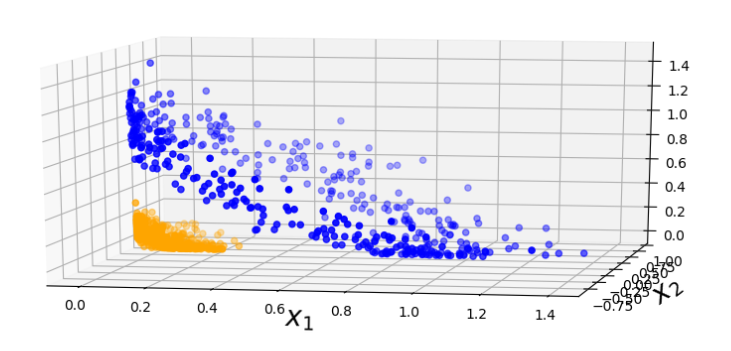
我们可以对数据进行很多转换，允许我们在更高维度上进行线性分离数据，但是并非这些功能实际上都是核。核函数具有特殊的属性，使其在训练支持向量模型中特别有用，并且在优化非线性支持向量分类器时使用此属性称为核技巧。

核技巧

我们已经看到了更高维的变换能够使我们分离数据并且进行预测。现在来看，为了训练支持向量分类器并且优化我们的目标函数，我们必须在变换后的特征空间中以更高维的向量执行运算。在实际应用中，数据可能会有很多的特征，并且设计这些特征的多项式组合的应用将导致很高的成本。

而核技巧就解决了这样一个问题。关键就是在核方法仅仅通过原始数据的观测值（在较低维空间中的数据）之间的一组成对相似性来表示的数据，不是通过映射变换来表示这些变换后的坐标在高维特征空间中得到的数据。
在核方法中，数据集是被成对相似比较的的核矩阵来表示的，其中的项()时被核函数定义的。这个核范数具有特殊的数学意义。内核函数作为一个修正过的点积：
我们的内核函数在原始较低维空间接收输入，并且在较高维空间中返回转换为向量的点积。即如果我们有数据点和一个映射关系,然后返回映射关系的点积：就是一个核函数。

例子

例如，下面说明了用于二阶多项式的内核技巧，并且在上图中的3-D变换可视化了此变换。变换后的向量的坐标时两个分量和的函数。因此，点积也将只包含分量和。内核函数还将接收输入并且返回实数。

这里的核函数就是.
核技巧的好处就是：我们在优化以适合更高维决策边界的目标函数仅包含变换后的特征向量的点积。因此，我们就可以使用内核函数来代替这些点积项，甚至不使用.

请记住，我们的数据只能作为向量线性分离 ϕ（X）在更高维度的空间中，我们正在此更高维度的空间中找到最优的分离超平面 无需计算或实际上甚至都不了解ϕ（x）。