在第一部分中，我们了解了SVM的目标。其目标是找到使余量最大化的超平面。
但是，我们如何计算该间隔呢？

SVM=Support Vector Machine

在支持向量机中，有单词向量。这意味着重要的是要很好地理解向量以及如何使用它们。
这里是我们今天所见的简短总结：

• 什么是向量？
  • 它的范数
  • 它的方向
• 如何增加和减少向量？
• 点积是什么？
• 如何将向量投影到另一个向量上？

在工具箱中拥有所有这些工具后，我们将看到：

• 超平面的方程是什么？
• 如何计算间隔？

  什么是向量

  如果我们定义一个点 A（3 ，4 ）,在 R 我们可以这样绘制它。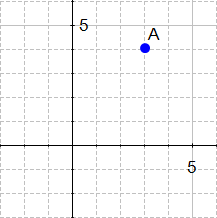
  
  定义：任何一点即从原点开始并以x结束的矢量。
  此定义意味着在原点和A之间存在一个向量。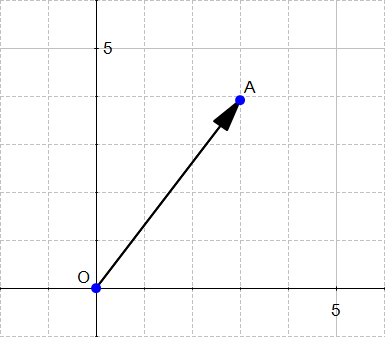
  
  1.向量的长度：
  向量长度的形式为||x||，称为范数。对于向量,就是它的长度

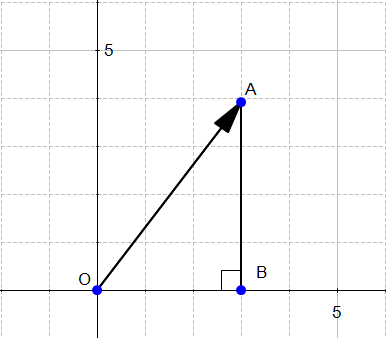
从图中，我们可以使用毕达哥拉斯定理轻松计算距离OA ：

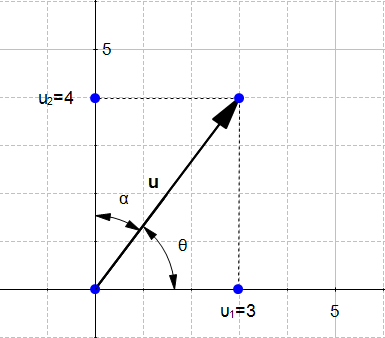
2.向量的方向：
方向是向量的第二个组成部分
定义：向量的方向为
w的坐标从哪得到？

了解定义

为了找到向量的方向，我们需要使用其角度。

图中我们显示了一个向量,其中

定义一

向量u的方向可以从x轴的或者y轴的来定义。
这很乏味。取而代之的是，我们将使用角度的余弦。
角度的余弦定义为：
在图4中，我们可以看到我们可以形成两个直角三角形，并且在两种情况下，相邻的边都将在一个轴上。这意味着余弦的定义隐含了与角度有关的轴。我们可以将定义改写为：

定义二

向量由被给定的的余弦值和的余弦值定义。现在我们看一下他们的定义：

这就是向量的原始定义。这就是为什么它的坐标也叫做方向余弦。

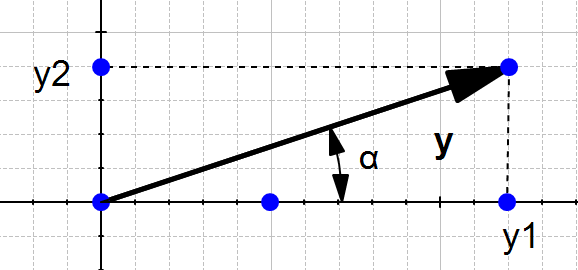
计算向量方向

从上图中计算的方向：

所以我们会说的方向为向量,在下图中画出这个向量。

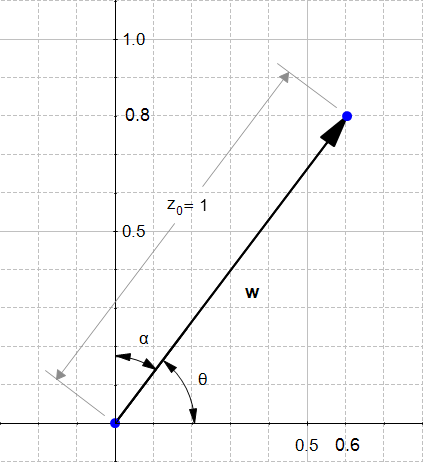
我们可以看到 确实和 除了较小。关于方向向量的一些有趣的东西 ww是它们的范数等于1。这就是为什么我们经常称它们为单位向量。

两个向量的和

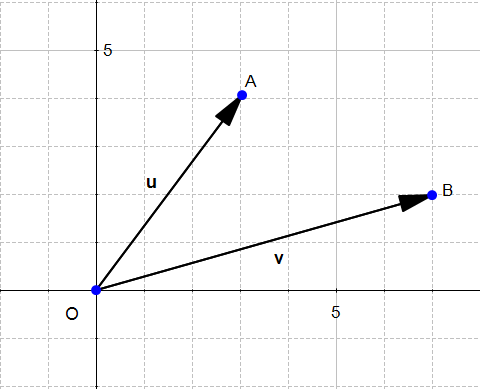
给定两个向量,他们两个的和为,这就证明了对应坐标的和就是向量相加的结果。

两个向量之差

类比于两个向量之和，两个向量之差为：

点积

代数形式的推导()

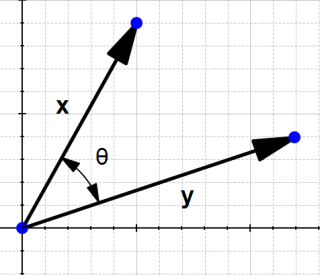
我们将X和y单独拿出来观察其结果：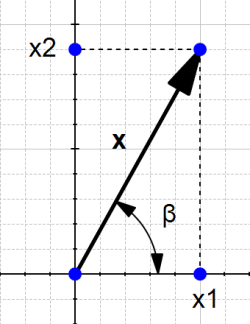

现在我们观察一下原始的结果：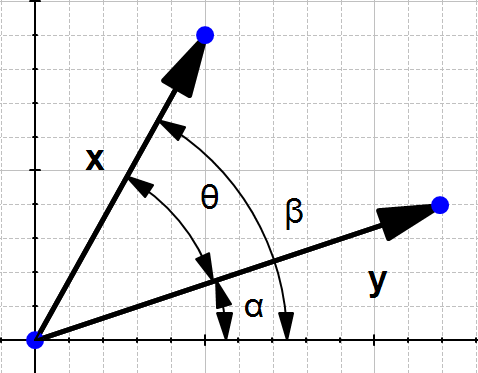

我们观察到,所以可以计算,并且通过长度计算余弦值

注意：上面定义中分别指的是在第一维(行)上的分量和在第二维(列)上的分量。
将余弦值带入其中替换：

两边都乘以||x||||y||就得到了
所以我们得到了点积的结果
往高维情况下类推得到点积结果形式为：

点积的总结

• 是一个内积
• 结算结果形式是一个标量

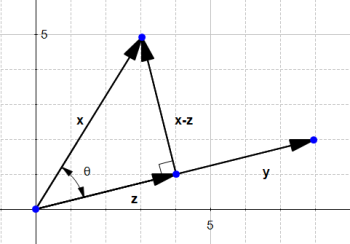
  几何形式推导(证明表明是x在y或者y在x上的投影)

  
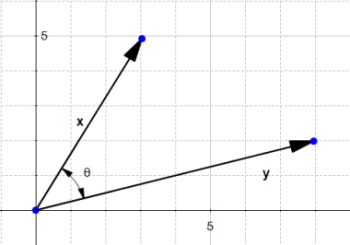
  给定了一个向量x和一个向量y，我们现在来看x投射在y上的长度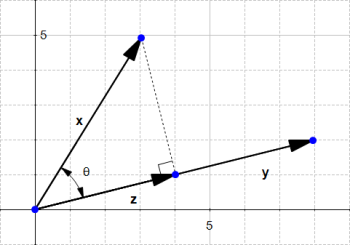
  
  投影完成以后得到向量z，由上面的定义得到：,由上述的点积结果我们知道了,将代替，得到，如果我们用代表的方向上的单位向量，即,所以我们可以看到，(因为我们最后要得到的是数值，所以需要转置相乘).
  其中的u是向量y的单位向量，所以也是z的单位向量，,可以得到,这个就是x投影在y上的z的长度大小。

从上图中，可以看到另一个长度

SVM超平面

我们在两个变量的情况下，一条直线是这样定义的：,但是我们平常看到的超平面的定义形式为：。第一种形式可以视为超平面的特殊形式，即 计算点积结果：,这两个结果是一样的，我们为什么要用
有两个原因：

• 使用这样一个定义我们能很简单地计算二维以上的数据
• 向量 W 将始终与超平面垂直（注意：关于最后一句话，我收到了很多疑问。 W总是正常的，因为我们使用此向量定义超平面，因此根据定义，它将是正常的。正如你可以看到 这个页面，当我们定义一个超平面，我们假定我们有一个向量垂直于超平面）

最后一个属性将很方便地计算从点到超平面的距离。

计算点到超平面的距离

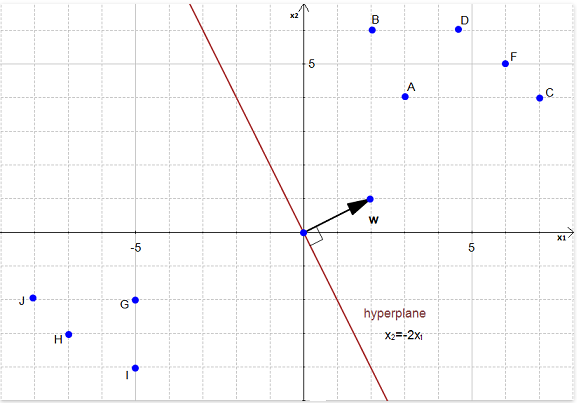
为了简化此实例，我们令=0,上述这个式子为,即
我们注意到向量w已经在图中表示了出来，如果我们想要知道点A（3，4）到达超平面的距离，这个便是A投射到超平面时的距离。
我们可以把A作为从原点到达A点的一个向量，我们将他映射到向量w上。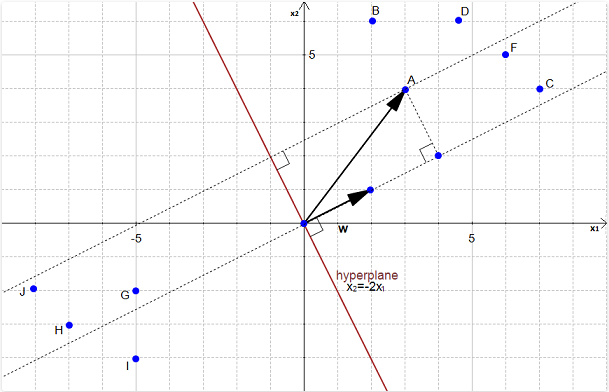

这个时候我们令A点投射到w上的点为P点，那么P点的长度就是A到超平面的距离。如下图所示

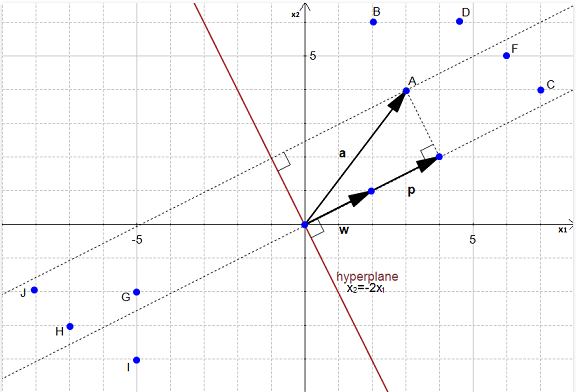
接下来就要求出p的长度，由上面我们的推导可知,其中u为p方向上的单位向量。
以上题目为例，可以得知代入其中解得

计算超平面的间隔

现在我们知道了A和超平面的距离为,间隔（margin）定义为：.至此，我们就计算出了超平面的间距