点到平面距离

在我看来，感知鸡就相当于弱化版的SVM，即在二维平面上实现正确分类即可。
感知机的方程

其中是超平面的法向量，是超平面的。例如，写成感知机方程为，查看其图形，截距为-1

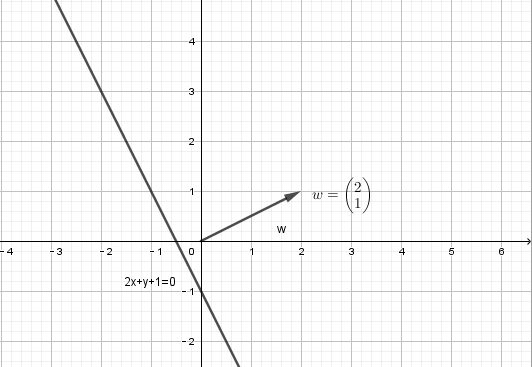
例如，写成感知机方程，其图形，截距为1

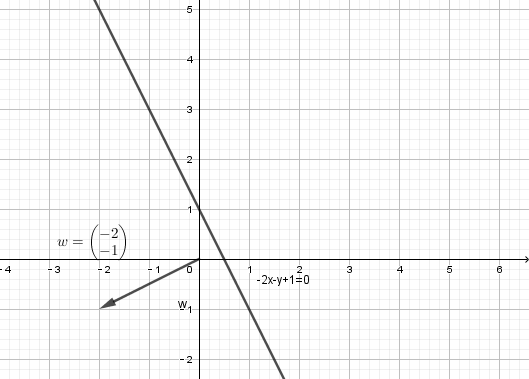
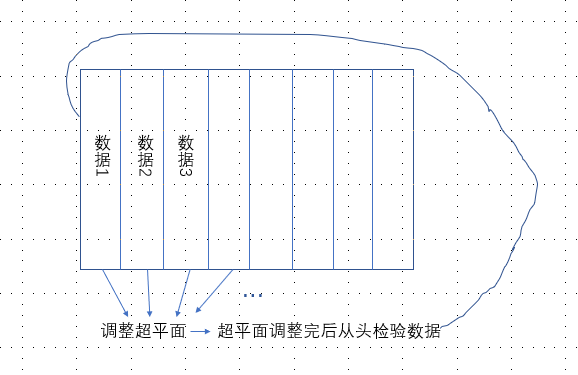
所以，能够完全把所有数据集分开的感知机模型如下图所示：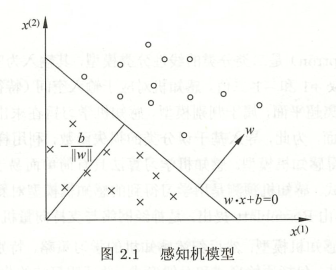

为此我们要找到一个损失函数，这个损失函数是所有误分类点到超平面的距离，这个距离我们来推导一下：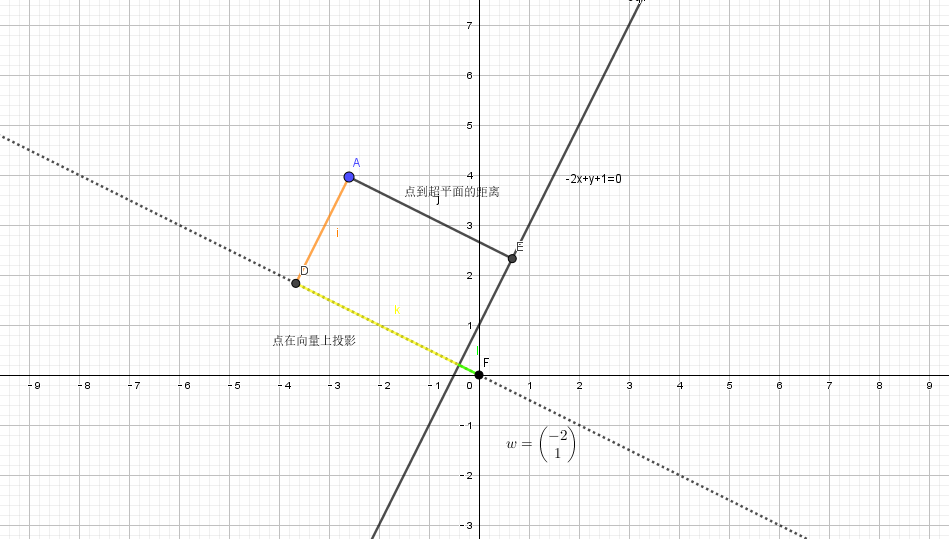

• 点A（）坐标为，可以得到点A在向量的基向量投影

= 点A到超平面的距离 + 原点到超平面的距离，所以要求的距离就变成了原点到超平面的距离。
原点到超平面的距离又等于点，即超平面与轴的交点在基向量上的投影，所以点A到超平面的距离为；

• 如果点A（），则。所以我们取绝对值

损失函数

损失函数：这里我们取得损失函数便成了所有误分类点到超平面的距离

在不考虑就是损失函数（不考虑的话就会存在无数解，如果想要得到唯一解，便是SVM的知识了。）

梯度下降法

由我们的损失函数可得，我们所要做的工作为最小化损失函数

损失函数的最小值为0，因为这时没有误分类点，所以距离为0.感知机学习算法是误分类驱动，采用随机梯度下降法。首先，任意选取一个超平面，然后用梯度下降法不断地极小化目标函数。极小化过程中不是一次使（误分类数据集）中所有误分类点的梯度下降，而是一次随机选取一个误分类点使其梯度下降。
假设误分类点集合是固定的，那么损失函数的梯度由

得到

其中是步长 ，又称学习率。

求解步骤

1. 选取初值
2. 选取数据
3. 判断，如果，则
4. 转到步骤2，继续判断数据

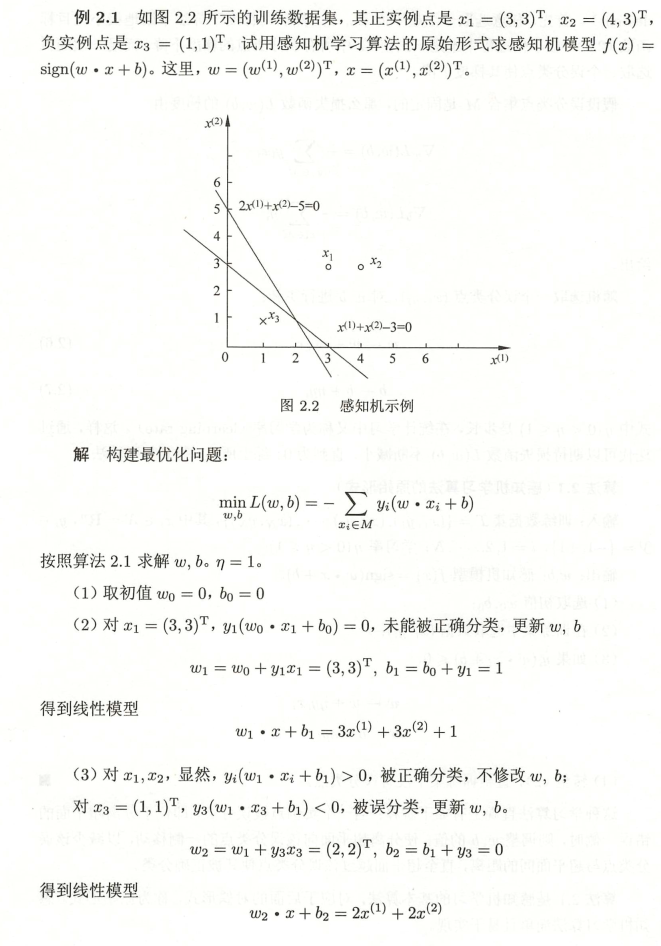
例子

代码

clear
clc
y = [1,1,-1];
x = [3,4,1;3,3,1];%每列代表一个数据集
scatter(x(1,:),x(2,:),'filled');
axis([0 5 ,-5 5])
X = 0:5;
%选出初值w0,b0
w = [0,0];
b = 0;
%选取学习率
eta = 1;
%选取数据(xi,yi)
column = 1;
while column <= size(x,2) 
    hold on
    flag = 0;
    while (y(column)*(w*x(:,column)+b) <0) || (y(column)*(w*x(:,column)+b) ==0)
        w = w + eta*y(column)*x(:,column)';
        b = b + eta*y(column);
        flag = 1 ;
    end
    Y = (-w(1)*X - b)/(w(2));
    plot(X,Y);
     column = column + 1;
     if flag == 1
         column = 1;
     end
     disp(column)
     pause(2)
end

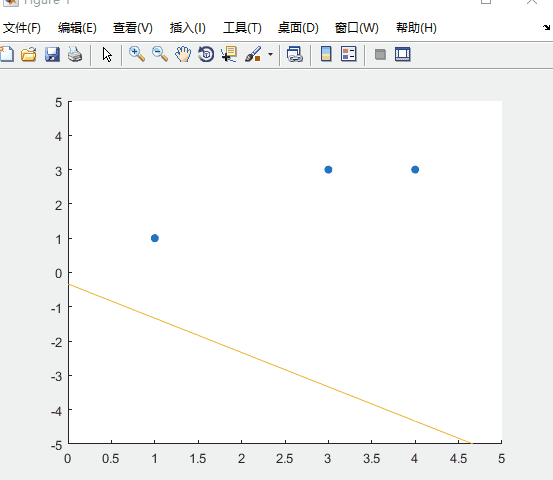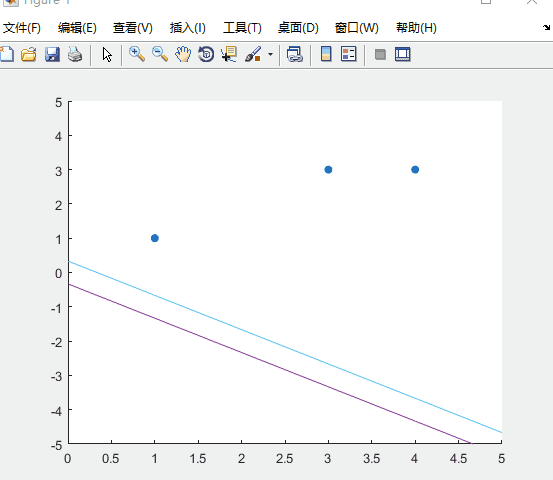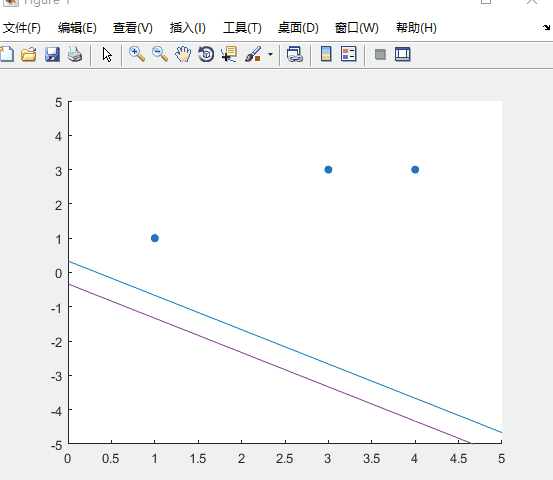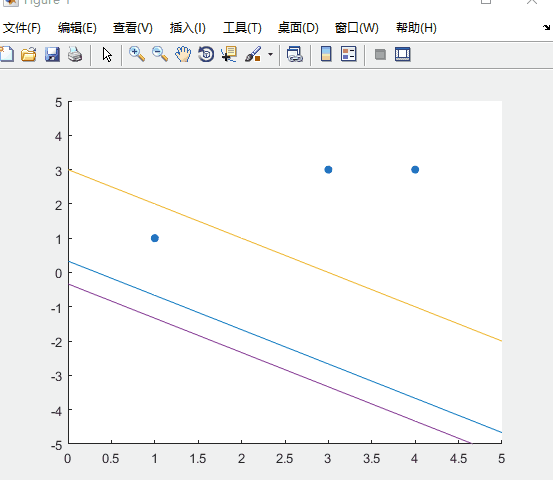
可以看到超平面的迭代过程