西瓜数据集3.0a:西瓜数据集3.0a.zip
第八章
8.1
假设硬币正面朝上的概率为,反面朝上的概率为
。令
代表抛
次硬币所得正面朝上的次数,则最多
次正面朝上的概率为
对,由Hoeffding不等式
试着推导出式子
解:
8.2
对于0/1损失函数来说,指数损失函数并非仅有的一致替代函数。考虑式子。试证明,任意损失函数
,若对于
在区间
上单调递减,则
是0/1损失函数的一致替代函数。(
是基分类器的线性组合)
解:是对
得单调递减函数,那么可以认为
是对
得单调递增函数。此时,
,即达到了贝叶斯最优错误率,所以
是0/1损失函数得一致替代函数。
8.3
从网上下载或自己编程实现AdaBoost,以不剪枝决策树为基学习器,在西瓜数据集3.0a上训练一个AdaBoost集成,并与图8.4进行比较。
8.4
GradientBoosting是一种常用的Boosting算法,试分析其与AdaBoost的异同。
解:
- 相同之处:GradientBoosting与AdaBoost相同的地方在于要生成多个分类器以及每个分类器都有一个权值,最后将所有分类器加权累加起来。
- 不同之处:AdaBoost通过每个分类器的分类结果改变每个样本的权值用于新的分类器和生成权值,但每个样本不会改变;GradinetBoosting将每个分类器对样本的预测值与真实值的差值传入下一个分类器来生成新的分类器和权值(这个差值就是下降方向),而每个样本的权值不变。
8.5
试变成实现Bagging,以决策树桩为基学习器,在西瓜数据集3.0a上训练一个Bagging集成,并与图8.6比较。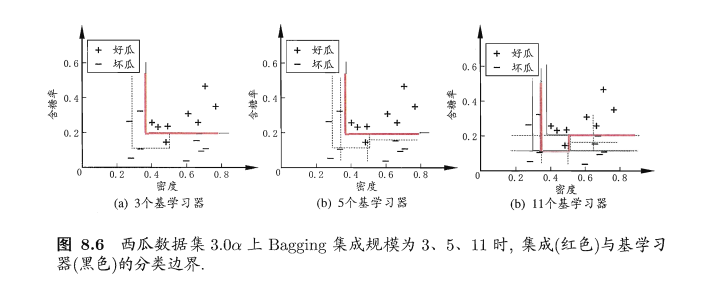
解:
(1)决策树桩:决策树桩是最简单的线性分类器,分类原理
决策树桩分类实例:
数据:5个拉拉队员的数据
| 拉拉队员 | 身高 | 体重 | 性别 |
|---|---|---|---|
| 1 | 170 | 55 | 男 |
| 2 | 160 | 45 | 女 |
| 3 | 180 | 65 | 男 |
| 4 | 165 | 50 | 女 |
| 5 | 170 | 50 | 女 |
如果我们想根据拉拉队员的身高体重对其进行分类,很明显,体重>50的都是男队员,体重<=50的都是女队员,剩下的工作就是让机器根据这些数据自己学习找到合适的阈值。设计出来的算法就是决策树桩的算法了。
为此,我们将问题更加细化以下,使用体重作为特征,性别作为标签进行分类(Y=1判别性别为男,Y=0判别性别为女)。
决策树桩的模型是找到一个一维的线性模型,因此其模型函数可以看作,其中
是阈值,我们规定,当
时,预测
,否则
。为了找到一个合适的阈值
使用最简单的线性搜索就可以解决,算法如下
L = 1; minErr = 99999; for t = min(x) to max(x) by L do numErr = numberOfErrors(t) if numErr <= minErr minErr = numErr tbest = t end if end for return tbest
在这个算法中,我们从的最小值开始搜索,直到
的最大值。每次更新
时给
增加
这么大。 numberOfErrors 函数用来统计我们在t作为阈值的情况下,分类的错误数目,这样搜索了一遍后,就能找到一个错误最少的tbest作为我们决策树桩的阈值。
其中学习步长的作用十分重要,如果
过大的话,可能会不小心错过最优解,但是L过小的话,又会导致算法运行时间过长。因此调整一个合适的L值是十分必要的。
(2)Bagging算法思想
- 1.给定一个弱学习算法,和一个训练集;
- 2.单个弱学习算法准确率不高;
- 3.将该学习算法使用多次,得出预测函数序列,进行投票;
- 4.最后结果准确率将得到提高.
(3)Bagging算法流程
(4)解题思路
(5)决策树桩选择合适的阈值来进行二分类的过程中时,怎么找到合适的阈值?
(别人的回答)
回答一:
- 首先对这个连续变量排序。比如说年龄,把所有样本中年龄的数值从小到大排序。
- 在数据没有重复的假设下,如果有n个样本,那么排序后的数据之间应该有n-1个间隔。
- 决策树会对这n-1个间隔进行逐一尝试(分叉),每个不同的分叉,会带来不同的gini指数,我们最终选gini指数最小的那个分叉作为最优分叉,也就是阈值。
理论上是这样进行的,但是实际情况是为了一些计算优化,可能会进行一些随机搜索,而不一定是遍历。
上面这个过程就把那个连续变量进行了一分为二(第一次离散化),比如说年龄被分成了0到20岁,20到100岁。
接下来,当决策树继续生长时,之前一分为二的连续特征可能会再次被选中。比如说20到100岁这个分叉被选中,我们再次重复上面那三个步骤,再去寻找下一个次分叉的阈值。这次得到的结果可能是20到35,35到100岁。
以此反复,这样一个连续变量就不停地被离散化,直到模型达到停止的条件。
回答二:
假如训练集上有Age这么个特征,数值分别为
10,11, 16, 18, 20, 35
那么在这个节点上,算法会自动考虑下面几种划分的可能
Age <=10 和 Age>10Age <=11 和 Age>11Age <=16 和 Age>16Age <=18 和 Age>18Age <=20 和 Age>20
六个数值点,所以就有5个对应划分的可能。对这5个可能一一尝试,选出损失函数最小的那个。
回答三:
对于数值特征,决策树会对所有取值一一尝试,直到选择到最好的。
对于分类,就是对应gini最小
对于回归,就是对应rmse最小
(6)基尼指数
基尼不纯度指标
在CART算法中,基尼不纯度表示一个随机选中的样本在子集中被分错的可能性。基尼不纯度为这个样本被选中的概率✖它被分错的概率。当一个节点中所有样本都是一个类时,基尼不纯度为零。
假设,令
是样本被赋予
的概率,则基尼指数可以通过如下计算:
例子链接:
| 有房者 | 婚姻状况 | 年收入 | 拖欠贷款者 |
|---|---|---|---|
| 是 | 单身 | 125k | 否 |
| 否 | 已婚 | 100k | 否 |
| 否 | 单身 | 70k | 否 |
| 是 | 已婚 | 120k | 否 |
| 否 | 离异 | 95k | 是 |
| 否 | 已婚 | 60k | 否 |
| 是 | 离异 | 220k | 否 |
| 否 | 单身 | 85k | 是 |
| 否 | 已婚 | 75k | 否 |
| 否 | 单身 | 90k | 是 |
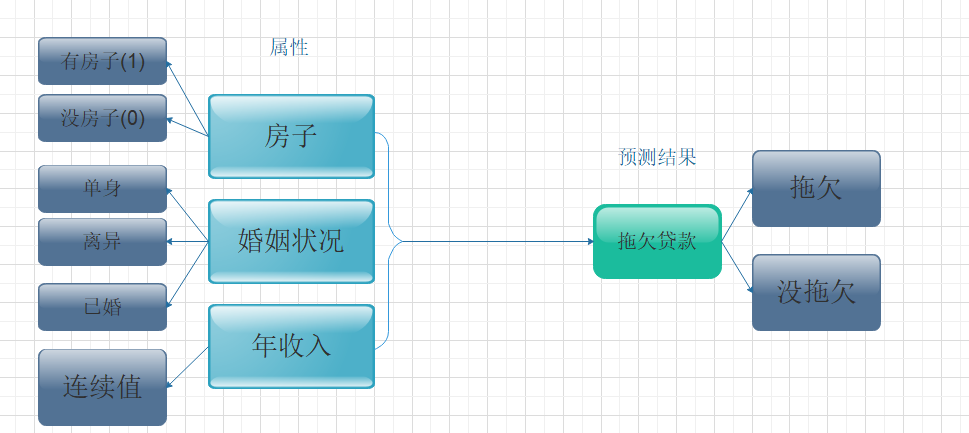
- 从房子属性来看 | | 有房 | 没房 | | —- | —- | —- | | 没贷款 | 3 | 4 | | 贷款 | 0 | 3 |
- 婚姻状况属性来看,它 的取值有三种 | | 单身或已婚 | 离异 | | —- | —- | —- | | 否 | 6 | 1 | | 是 | 2 | 1 |
| 单身或离异 | 已婚 | |
|---|---|---|
| 否 | 3 | 4 |
| 是 | 3 | 0 |
| 离异或已婚 | 单身 | |
|---|---|---|
| 否 | 5 | 2 |
| 是 | 1 | 2 |
- 从年入属性来看,它是一个连续的属性,连续的取值采用分裂点进行分裂
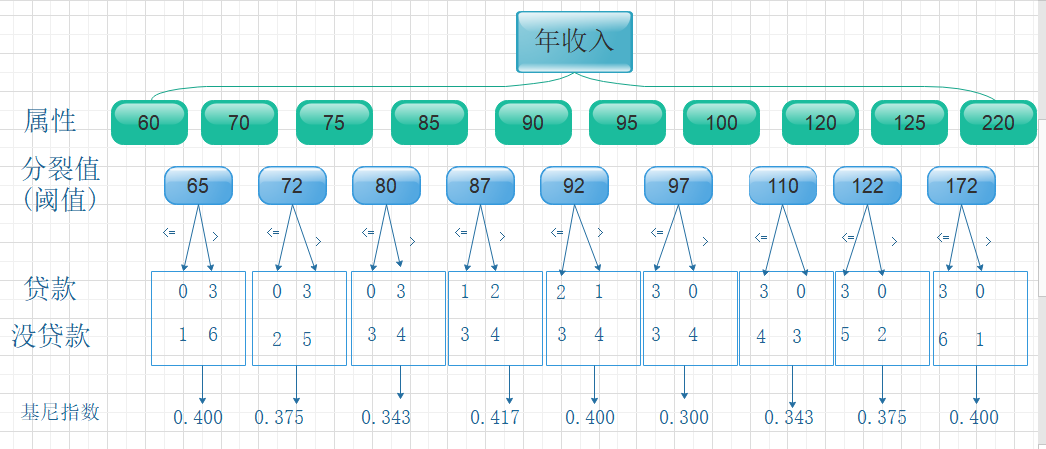
所以找对阈值为97时的Gini指数最小。
(7)代码:
计算密度的最优分类阈值和信息增益:
function [threshold_optimal,entropy_add,data_result] = density(data)%因为有含糖率和密度两个属性,所以要用ID3来判断这部分,单独写一个函数% clear;% clc;% load('dataset.mat');% data = watermelon;%根据Gini指数找到合适的阈值点[density_matrix,position] = sort(data(:,1));%根据位置信息找到排序后的结果density_matrix = [density_matrix,data(position,3)];%设定阈值矩阵for i = 1:size(density_matrix,1)-1threshold_matrix(i) = (density_matrix(i)+density_matrix(i+1))/2;endfor i = 1:length(threshold_matrix)threshold_small_bad_watermelon_number = 0;threshold_small_good_watermelon_number = 0;threshold_big_bad_watermelon_number = 0;threshold_big_good_watermelon_number = 0;for j = 1:size(density_matrix,1)if density_matrix(j,1)<threshold_matrix(i) || density_matrix(j,1) == threshold_matrix(i)if density_matrix(j,2) ==1threshold_small_good_watermelon_number = threshold_small_good_watermelon_number+1;elsethreshold_small_bad_watermelon_number = threshold_small_bad_watermelon_number+1;endendif density_matrix(j,1)>threshold_matrix(i)if density_matrix(j,2) == 1threshold_big_good_watermelon_number = threshold_big_good_watermelon_number+1;elsethreshold_big_bad_watermelon_number = threshold_big_bad_watermelon_number+1;endendend%计算基尼指数%因为式子太长,所以简化tsgwn = threshold_small_good_watermelon_number;同理tsgwn = threshold_small_good_watermelon_number;tsbwn = threshold_small_bad_watermelon_number;tbgwn = threshold_big_good_watermelon_number;tbbwn = threshold_big_bad_watermelon_number;threshold_sum = tsgwn+tsbwn+tbgwn+tbbwn;Gini_index_small = 1-(tsgwn/(tsgwn+tsbwn))^2-(tsbwn/(tsgwn+tsbwn))^2;Gini_index_big = 1-(tbgwn/(tbgwn+tbbwn))^2-(tbbwn/(tbgwn+tbbwn))^2;Gini_index = (tsgwn+tsbwn)/(threshold_sum)*(Gini_index_small)+(tbgwn+tbbwn)/(threshold_sum)*(Gini_index_big);Gini_index_matrix(i) = Gini_index;end%找到最小的基尼指数,然后找到阈值[Gini_index_minimum,position] = min(Gini_index_matrix);threshold_optimal = threshold_matrix(position);% 找到最优阈值下的信息熵%计算好瓜和坏瓜的信息熵good_watermelon = 0;bad_watermelon = 0;for j=1:size(data,1)if data(j,3) == 1good_watermelon = good_watermelon+1;elsebad_watermelon = bad_watermelon+1;endendp_good_watermelon = good_watermelon/(size(data,1));p_bad_watermelon = bad_watermelon/(size(data,1));information_entropy = -p_good_watermelon*mylog(p_good_watermelon)-p_bad_watermelon*mylog(p_bad_watermelon);% tsgw 是 threshold_small_good_watermelon的缩写%tsgw = 0;tsbw = 0;tbgw = 0;tbbw = 0;for i = 1:size(data,1)if density_matrix(i,1) < threshold_optimalif density_matrix(i,2) == 1tsgw = tsgw+1;elsetsbw = tsbw+1;endelseif density_matrix(i,2) == 1tbgw = tbgw+1;elsetbbw = tbbw+1;endendenddisp(tsgw);disp(tsbw);disp(tbgw);disp(tbbw);entropy_threshold_small = -(tsbw/(tsbw+tsgw))*mylog(((tsbw)/(tsbw+tsgw)))-(tsgw/(tsbw+tsgw))*mylog(tsgw/(tsbw+tsgw));entropy_threshold_big = -(tbbw/(tbbw+tbgw))*mylog(((tbbw)/(tbbw+tbgw)))-(tbgw/(tbbw+tbgw))*mylog(tbgw/(tbbw+tbgw));entropy_threshold = (tsgw +tsbw)/(tsgw+tsbw+tbgw+tbbw)*entropy_threshold_small+(tbgw+tbbw)/(tsgw+tsbw+tbgw+tbbw)*entropy_threshold_big;entropy_add = information_entropy - entropy_threshold;disp('信息增益');disp(entropy_add);%计算分类结果% data_result(:,1) = data(:,1);for i=1:size(data,1)if data(i,1) <threshold_optimal || data(i,1) == threshold_optimaldata_result(i,1) = -1;elsedata_result(i,1) = 1;endendend
最优阈值:0.3815;信息增益:0.1819
计算含糖率的最优阈值和信息增益:代码同上(只需要修改数据)
function [threshold_optimal,entropy_add,data_result] = sugar(data)%因为有含糖率和密度两个属性,所以要用ID3来判断这部分,单独写一个函数% clear;% clc;% load('dataset.mat');% data = watermelon;% step_length = 0.01;%根据Gini指数找到合适的阈值点[sugar_matrix,position] = sort(data(:,2));%根据位置信息找到排序后的结果sugar_matrix = [sugar_matrix,data(position,3)];%设定阈值矩阵for i = 1:size(sugar_matrix,1)-1threshold_matrix(i) = (sugar_matrix(i)+sugar_matrix(i+1))/2;endfor i = 1:length(threshold_matrix)threshold_small_bad_watermelon_number = 0;threshold_small_good_watermelon_number = 0;threshold_big_bad_watermelon_number = 0;threshold_big_good_watermelon_number = 0;for j = 1:size(sugar_matrix,1)if sugar_matrix(j,1)<threshold_matrix(i) || sugar_matrix(j,1) == threshold_matrix(i)if sugar_matrix(j,2) ==1threshold_small_good_watermelon_number = threshold_small_good_watermelon_number+1;elsethreshold_small_bad_watermelon_number = threshold_small_bad_watermelon_number+1;endendif sugar_matrix(j,1)>threshold_matrix(i)if sugar_matrix(j,2) == 1threshold_big_good_watermelon_number = threshold_big_good_watermelon_number+1;elsethreshold_big_bad_watermelon_number = threshold_big_bad_watermelon_number+1;endendend%计算基尼指数%因为式子太长,所以简化tsgwn = threshold_small_good_watermelon_number;同理tsgwn = threshold_small_good_watermelon_number;tsbwn = threshold_small_bad_watermelon_number;tbgwn = threshold_big_good_watermelon_number;tbbwn = threshold_big_bad_watermelon_number;threshold_sum = tsgwn+tsbwn+tbgwn+tbbwn;Gini_index_small = 1-(tsgwn/(tsgwn+tsbwn))^2-(tsbwn/(tsgwn+tsbwn))^2;Gini_index_big = 1-(tbgwn/(tbgwn+tbbwn))^2-(tbbwn/(tbgwn+tbbwn))^2;Gini_index = (tsgwn+tsbwn)/(threshold_sum)*(Gini_index_small)+(tbgwn+tbbwn)/(threshold_sum)*(Gini_index_big);Gini_index_matrix(i) = Gini_index;end%找到最小的基尼指数,然后找到阈值[Gini_index_minimum,position] = min(Gini_index_matrix);threshold_optimal = threshold_matrix(position);% 找到最优阈值下的信息熵%计算好瓜和坏瓜的信息熵good_watermelon = 0;bad_watermelon = 0;for j=1:size(data,1)if data(j,3) == 1good_watermelon = good_watermelon+1;elsebad_watermelon = bad_watermelon+1;endendp_good_watermelon = good_watermelon/(size(data,1));p_bad_watermelon = bad_watermelon/(size(data,1));information_entropy = -p_good_watermelon*mylog(p_good_watermelon)-p_bad_watermelon*mylog(p_bad_watermelon);% tsgw 是 threshold_small_good_watermelon的缩写%tsgw = 0;tsbw = 0;tbgw = 0;tbbw = 0;for i = 1:size(data,1)if sugar_matrix(i,1) < threshold_optimalif sugar_matrix(i,2) == 1tsgw = tsgw+1;elsetsbw = tsbw+1;endelseif sugar_matrix(i,2) == 1tbgw = tbgw+1;elsetbbw = tbbw+1;endendenddisp(tsgw);disp(tsbw);disp(tbgw);disp(tbbw);entropy_threshold_small = -(tsbw/(tsbw+tsgw))*mylog(((tsbw)/(tsbw+tsgw)))-(tsgw/(tsbw+tsgw))*mylog(tsgw/(tsbw+tsgw));entropy_threshold_big = -(tbbw/(tbbw+tbgw))*mylog(((tbbw)/(tbbw+tbgw)))-(tbgw/(tbbw+tbgw))*mylog(tbgw/(tbbw+tbgw));entropy_threshold = (tsgw +tsbw)/(tsgw+tsbw+tbgw+tbbw)*entropy_threshold_small+(tbgw+tbbw)/(tsgw+tsbw+tbgw+tbbw)*entropy_threshold_big;entropy_add = information_entropy - entropy_threshold;disp('信息增益');disp(entropy_add)for i=1:size(data,2)if data(i,2) <threshold_optimal || data(i,2) == threshold_optimaldata_result(i,1) = -1;elsedata_result(i,1) = 1;endendend
最优阈值:0.2045;信息增益:0.2337
其中的mylog函数,是由于所以重写的
function y = mylog(x)if x==0y=0;elsey = log(x);endend
自主采样法,抽出个数据集
function [s,t]=zizhu(data)t = data;[m,n] = size(data);s = zeros(m,n);labels = [];for i=1:mindex = UNIDRND(m);labels = [labels index];s(i,:) = data(index,:);endkind=unique(labels);disp(length(kind))t(kind,:) = [];
接下来通过个数据集得到
个分类器,可以把上面的密度和含糖率的阈值和信息增益计算写成函数来调用
clear;clc;load('dataset.mat');data = watermelon;data_initial = data;data_update = data;T=5;for t = 1:Tdensity_data_result_matrix(:,1) = data_initial(:,1);data_random = zizhu(data_initial(:,1));data_update(:,1) = data_random;[threshold,entropy,data_result] = density(data_update);density_threshold_matrix(t) = threshold;density_data_result_matrix(:,t+1) = data_result;endxlswrite('C:\Users\25626\Desktop\density_data_result_matrix.xlsx',density_data_result_matrix');for t = 1:Tsugar_data_result_matrix(:,1) = data_initial(:,2);data_random1 = zizhu(data_initial(:,2));data_update(:,2) = data_random1;[threshold,entropy,data_result1] = sugar(data_update);sugar_threshold_matrix(t) = threshold;sugar_data_result_matrix(:,t+1) = data_result1;endxlswrite('C:\Users\25626\Desktop\sugar_data_result_matrix.xlsx', sugar_data_result_matrix');
最后的预测结果
使用随机的抽样数据得出的结果:
密度
| 阈值\样本 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.6770 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | 1 | 1 | -1 | -1 | -1 | -1 | 1 | 1 |
| 0.2940 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | -1 | 1 | -1 | -1 | -1 | 1 | 1 |
| 0.7080 | -1 | 1 | -1 | 1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 |
| 0.2940 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | -1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0.6080 | 1 | 1 | -1 | -1 | 1 | 1 | -1 | 1 | -1 | -1 | -1 | -1 | 1 | -1 | -1 | 1 | -1 |
含糖率
| 阈值\样本 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.2655 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | 1 | 1 | -1 | 1 | -1 | -1 | 1 | -1 | 1 | -1 |
| 0.0740 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | -1 | -1 | -1 | 1 | 1 | 1 | 1 |
| 0.0420 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | -1 | 1 | -1 |
| 0.2640 | 1 | 1 | 1 | 1 | -1 | -1 | 1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 |
| 0.3700 | -1 | -1 | 1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 |
最后还差一个投票输出的代码,but I’m lazy 。这个比较简单。
。这个比较简单。
8.6
试着分析Bagging通常为何难以提升朴素贝叶斯分类器的性能。
解:
Bagging主要是降低分类器的方差,而朴素贝叶斯分类器没有方差可以减少。对全训练样本生成的朴素贝叶斯分类器是最优的分类器,不能随机抽样来提高泛化性能。
8.7
试着分析随机森林为什么比决策树Bagging集成的训练速度更快。
解:
随机森林不仅会随机样本,还会在所有样本属性中随机集中出来计算。这样每次生成分类器时都是对部分属性计算最优,速度会比Bagging计算全属性要快。
8.8
MultiBosting算法将AdaBoost作为Bagging学习的基学习器,Iterative Bagging算法则是将Bagging作为AdaBoost的基学习器。试着比较二者的优缺点。
解:
MultiBoosting由于集成了Bagging,Wagging,AdaBoost,可以有效的降低误差和方差,特别是误差。但是训练样本和预测成本都会显著增加
Iterative Bagging相比Bagging会降低误差,但是方差上升。由于Bagging本身就是一种降低方差的算法,所以Iterative Bagging相当于Bagging与单分类器的折中。
8.9
试着设计一种可视化的多样性度量,对习题8.3和习题8.5中得到的集成进行评估,并与-误差图比较。
8.10
试着设计一种能提升近邻分类器性能的集成学习算法。
解:
可以使用Bagging来提升近邻分类器的性能,每次随机抽取出一个子样本,并训练一个
近邻分类器,对测试样本进行分类,最终投票得到最多的一种分类。

