KNN介绍
k近邻法(k-nearest neighbors)是由Cover和Hart于1968年提出的,它是懒惰学习(Lazy learning)的著名代表。它的工作机制比较简单:
- 给定一个测试样本
- 计算它到训练样本的距离
- 距离测试样本最近的
个训练样本
- “投票法”选出在这
个样本中出现类别最多的类别,就是预测的结果
距离衡量的标准有很多,常见的有:距离、切比雪夫距离、马氏距离、巴士距离、余弦值等。
什么意思,看这张图。
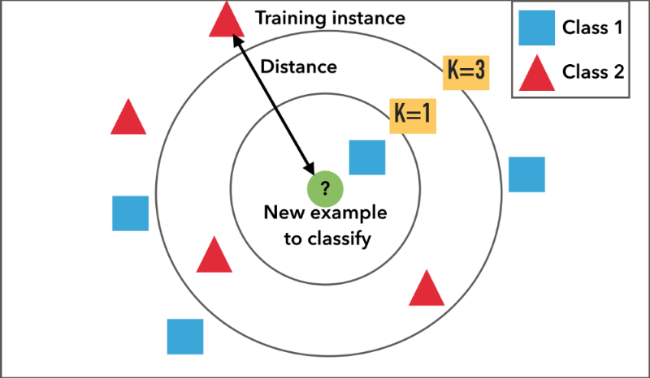
我们对应上面的流程来说
- 1.给定了红色和蓝色训练样本,绿色为测试样本
- 2.计算绿色点到其他点的距离
- 3.选取绿色点最近的
个点
- 4.选取
个点中,同种颜色最多的类.例如:
时,
的点全是蓝色,那么预测结果就是
;
时,
个点中有两个为红色点,故结果就为
举例
这里用欧氏距离作为距离的衡量标准,用鸢尾花数据集进行举例证明.
鸢尾花数据集有三个类别,每个类有150个样本,每个样本有四个特征.
先来回顾欧式距离的定义:
在欧几里得空间中,点和
之间的欧式距离为:
向量的自然长度,即该点到原点的距离为:
.在欧几里得度量下,两点之间线段最短.
现在给出六个训练样本,分为三类,每个样本有四个特征,编号为7的名称是我们需要预测的.
| 编号 | 花萼长度(cm) | 花萼宽度(cm) | 花瓣长度(cm) | 花瓣宽度(cm) | 名称 |
|---|---|---|---|---|---|
| 1 | 4.9 | 3.1 | 1.5 | 0.1 | Iris setosa |
| 2 | 5.4 | 3.7 | 1.5 | 0.2 | Iris setosa |
| 3 | 5.2 | 2.7 | 3.9 | 1.4 | Iris versicolor |
| 4 | 5.0 | 2.0 | 3.5 | 1.0 | Iris versicolor |
| 5 | 6.3 | 2.7 | 4.9 | 1.8 | Iris virginica |
| 6 | 6.7 | 3.3 | 5.7 | 2.1 | Iris virginica |
| 7 | 5.5 | 2.5 | 4.0 | 1.3 | ? |
根据之前说的步骤,我们计算测试样本到各个训练样本的距离.例如训练样本中编号1和测试样本的距离.
实现代码:
%KNN-数据集(使用矩阵)clearclcdata = [4.9,3.1,1.5,0.1,1;5.4,3.7,1.5,0.2,1;5.2,2.7,3.9,1.4,2;5.0,2.0,3.5,1.0,2;6.3,2.7,4.9,1.8,3;6.7,3.3,5.7,2.1,3;5.5,2.5,4.0,1.3,0];Distance = zeros(6,4);O_Distance = zeros(6,2);for i =1:6for j=1:4distance = data(i,j)-data(7,j);Distance(i,j) = distance;endendO_Distance = sqrt(sum(Distance.*Distance,2));O_Distance(:,2)=data(1:6,5);%O_Distance = sort(O_Distance);for i=1:length(O_Distance)for j=1:length(O_Distance)-iif O_Distance(j,1)>O_Distance(j+1,1)temp=O_Distance(j,:);O_Distance(j,:)=O_Distance(j+1,:);O_Distance(j+1,:)=temp;endendend
结果
为了方便,用1代替Iris setosa,2代替Iris versicolor,3代替Iris virginica.最后结果如图所示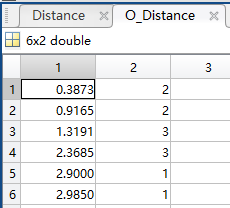
从中可以看出,如果选择的话,预测结果为2(Iris versicolor)
优缺点
优点
- 简单好用,容易理解,精度高,理论成熟,既可以用来分类也可以用来回归;
- 可用于数值型数据和离散型数据
- 训练时间复杂度为O(n);无数据输入假定;
-
缺点
计算复杂性高,空间复杂度高;
- 样本不平衡问题(即有些类别的样本数量很多,而其他样本数量很少)
- 一般数值很大的时候不用这个,计算量太大,但是单个样本又不能太少,否则容易发生误分.
- 最大的缺点是无法给出数据的内在含义.
补充:由于它属于懒惰学习,因此需要大量的空间来存储训练实例.在预测时它还需要与所有已知实例进行比较,增大了计算量.下图展示了当样本不平衡时的影响.
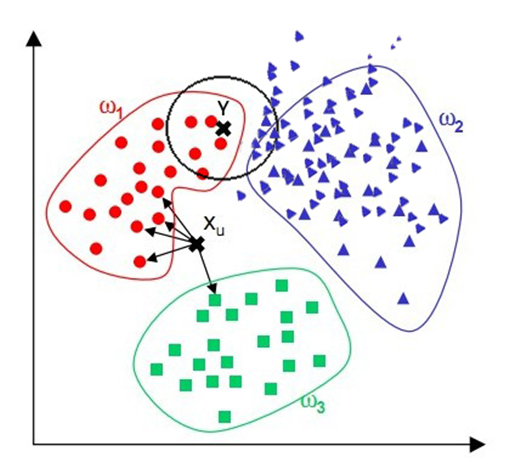
从直观上看出X应该是属于,这是理所当然的.对于Y应该属于
,但事实上在
范围内,更多的点属于
,这个就造成了错误分类.
一个结论
在周志华的机器学习中,证明了最近邻学习器的繁华错误率不超过贝叶斯最优分类器的错误率的两倍.
代码部分
转换为矩阵运算实现(L)
记测试集矩阵P的大小为M*D,训练集矩阵C的大小为N*D(测试集中共有M个点,每个点为D维特征向量.训练集中共有N个点,每个点为D维特征向量).
记是P的第
行:
,记
是C的第
行:
.
- 首先计算
和
之间的距离

