1. clear
  2. clc
  3. A=[1,1;1,1;0,0];
  4. [eigenvectors,eigenvaluesmatrix] = eig(A*A');
  5. %得到前后排序的位置变化，便于改变向量
  6. [eigenvaluesmatrix,position]=sort(diag(eigenvaluesmatrix),'descend');
  7. eigenvectors = eigenvectors(:,position);%将向量按照原来的循序重新排列
  8. U = eigenvectors;
  10. [eigenvectors,eigenvaluesmatrix] = eig(A'*A);
  11. [eignvaluesmatrix,position]=sort(diag(eigenvaluesmatrix),'descend');
  12. eigenvectors = eigenvectors(:,position);%将向量按照原来的循序重新排列
  13. V = eigenvectors;
  14. sum = sqrt(sort(diag(eigenvaluesmatrix),'descend')).*eye(size(A'*A,1));
  15. zero = zeros(size(A*A',1)-size(A'*A,1),size(A'*A,1));
  16. sum = [sum;zero];
  17. A_1 =U*sum*V'; 
  18. if A == int8(A_1)
  19.     disp('分解成功')
  20. else
  21.     disp('分解失败')
  22. end

怎么降维？

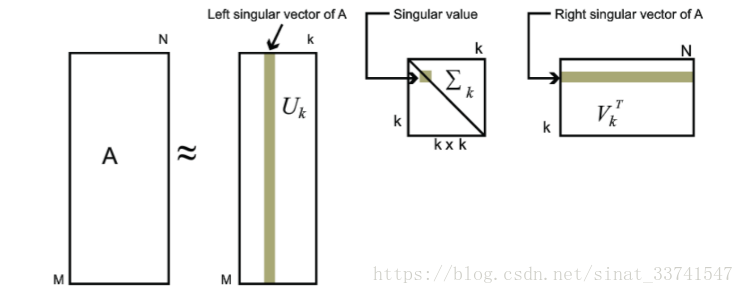
事实上，奇异值分解体现在其低秩逼近问题上，在这里也成为截断奇异值分解（Truncated SVD）。对于奇异值，按照惯例，我们通常降序排列§ matlab实现 - 图2的元素，而奇异值拥有一种特征，它减少的速度非常的快，通常前10%甚至1%的奇异值的和就占了全部奇异值之和的99%以上（即在这个方向投影最大），也即是我们可以用前面出现的K个奇异值和对应的奇异向量来近似的描述矩阵，即：
§ matlab实现 - 图3
在这里k要比n要小得多，如下图所示：

§ matlab实现 - 图4鸢尾花数据集降维

Iris.zip
鸢尾花数据为150X5的，只取2：5列的数据，然后进行降维，这时候的特征值为4个，所以我只取1个降维。

  1. function PCA(A,k)
  2. [eigenvectors,eigenvaluesmatrix] = eig(A*A');
  3. %得到前后排序的位置变化，便于改变向量
  4. [eigenvaluesmatrix,position]=sort(diag(eigenvaluesmatrix),'descend');
  5. eigenvectors = eigenvectors(:,position);%将向量按照原来的循序重新排列
  6. U = eigenvectors;
  8. [eigenvectors,eigenvaluesmatrix] = eig(A'*A);
  9. [eignvaluesmatrix,position]=sort(diag(eigenvaluesmatrix),'descend');
  10. eigenvectors = eigenvectors(:,position);%将向量按照原来的循序重新排列
  11. V = eigenvectors;
  12. sum = sqrt(sort(diag(eigenvaluesmatrix),'descend')).*eye(size(A'*A,1));
  13. zero = zeros(size(A*A',1)-size(A'*A,1),size(A'*A,1));
  14. sum = [sum;zero];
  15. A_1 =U(:,1:k)*sum(1:k,1:k)*V(:,1:k)'; 
  16. disp(A_1);
  17. % if A == int8(A_1)
  18. %     disp('分解成功')
  19. % else
  20. %     disp('分解失败')
  21. % end
  22. end

PCA(num(:,2:5),1)
4.4411 2.2454 3.0339 0.9925
4.1856 2.1162 2.8593 0.9354
4.0912 2.0685 2.7949 0.9144
4.0834 2.0645 2.7895 0.9126
4.4132 2.2313 3.0148 0.9863
4.8653 2.4599 3.3237 1.0874
4.1430 2.0947 2.8302 0.9259
4.3947 2.2219 3.0022 0.9822
3.8749 1.9591 2.6471 0.8660
4.2400 2.1437 2.8965 0.9476
4.7059 2.3793 3.2148 1.0517
4.3203 2.1844 2.9514 0.9656
4.1165 2.0813 2.8122 0.9200
3.7188 1.8802 2.5404 0.8311
4.9016 2.4782 3.3485 1.0955
5.1001 2.5786 3.4841 1.1398
4.7111 2.3819 3.2183 1.0529
4.4537 2.2518 3.0425 0.9954
4.9934 2.5247 3.4112 1.1160
4.5778 2.3145 3.1273 1.0231
4.6974 2.3750 3.2090 1.0498
4.5619 2.3065 3.1164 1.0195
4.0333 2.0392 2.7553 0.9014
4.5375 2.2941 3.0997 1.0141
4.4360 2.2428 3.0304 0.9914
4.3191 2.1837 2.9505 0.9653
4.4584 2.2542 3.0457 0.9964
4.5360 2.2934 3.0987 1.0138
4.4690 2.2595 3.0529 0.9988
4.2069 2.1270 2.8739 0.9402
4.2348 2.1411 2.8929 0.9464
4.6456 2.3488 3.1736 1.0382
4.6946 2.3736 3.2070 1.0492
4.8665 2.4605 3.3245 1.0876
4.2400 2.1437 2.8965 0.9476
4.2220 2.1346 2.8842 0.9436
4.6282 2.3400 3.1617 1.0344
4.2400 2.1437 2.8965 0.9476
3.8649 1.9541 2.6403 0.8638
4.4511 2.2505 3.0407 0.9948
4.3587 2.2037 2.9776 0.9741
3.7342 1.8880 2.5510 0.8346
3.9219 1.9829 2.6792 0.8765
4.5122 2.2813 3.0824 1.0084
4.7446 2.3989 3.2412 1.0604
4.1418 2.0941 2.8294 0.9256
4.6037 2.3276 3.1450 1.0289
4.0733 2.0595 2.7827 0.9104
4.6495 2.3508 3.1763 1.0391
4.3276 2.1880 2.9563 0.9672
6.8509 3.4638 4.6801 1.5311
6.4479 3.2600 4.4048 1.4410
6.8557 3.4662 4.6834 1.5322
5.4653 2.7633 3.7336 1.2215
6.4287 3.2503 4.3917 1.4368
5.9136 2.9899 4.0398 1.3216
6.5097 3.2913 4.4470 1.4549
4.8477 2.4510 3.3116 1.0834
6.4885 3.2805 4.4325 1.4501
5.3842 2.7223 3.6782 1.2033
4.8671 2.4608 3.3249 1.0877
5.9931 3.0301 4.0941 1.3394
5.6811 2.8723 3.8810 1.2697
6.2575 3.1638 4.2747 1.3985
5.5387 2.8004 3.7837 1.2379
6.5375 3.3053 4.4660 1.4611
5.9394 3.0030 4.0574 1.3274
5.7494 2.9069 3.9277 1.2849
6.0497 3.0587 4.1328 1.3521
5.5151 2.7884 3.7675 1.2326
6.3192 3.1950 4.3169 1.4123
5.9465 3.0065 4.0623 1.3290
6.3459 3.2085 4.3351 1.4183
6.2037 3.1366 4.2380 1.3865
6.2600 3.1650 4.2764 1.3990
6.4525 3.2624 4.4080 1.4421
6.6625 3.3685 4.5514 1.4890
6.7780 3.4270 4.6303 1.5148
6.1366 3.1026 4.1921 1.3715
5.4332 2.7470 3.7116 1.2143
5.3916 2.7260 3.6832 1.2050
5.3404 2.7001 3.6482 1.1935
5.6976 2.8807 3.8922 1.2734
6.3234 3.1971 4.3198 1.4132
5.8266 2.9459 3.9803 1.3022
6.2918 3.1811 4.2982 1.4062
6.6657 3.3702 4.5536 1.4897
6.0709 3.0694 4.1473 1.3568
5.7600 2.9122 3.9349 1.2873
5.5224 2.7921 3.7726 1.2342
5.6925 2.8781 3.8888 1.2722
6.2475 3.1587 4.2679 1.3963
5.7076 2.8857 3.8991 1.2756
4.8756 2.4651 3.3307 1.0896
5.7130 2.8885 3.9027 1.2768
5.8424 2.9539 3.9911 1.3057
5.8265 2.9458 3.9803 1.3022
6.1471 3.1080 4.1993 1.3738
4.8860 2.4704 3.3378 1.0920
5.7594 2.9119 3.9344 1.2872
7.1243 3.6020 4.8669 1.5922
6.2484 3.1592 4.2685 1.3965
7.4011 3.7420 5.0560 1.6541
6.7677 3.4217 4.6233 1.5125
7.0366 3.5577 4.8070 1.5726
7.9531 4.0210 5.4330 1.7774
5.4270 2.7439 3.7074 1.2129
7.6018 3.8434 5.1931 1.6989
6.9564 3.5171 4.7522 1.5547
7.7562 3.9215 5.2986 1.7334
6.7986 3.4374 4.6444 1.5194
6.6640 3.3693 4.5525 1.4894
7.0776 3.5784 4.8350 1.5818
6.1090 3.0887 4.1733 1.3653
6.3400 3.2055 4.3311 1.4169
6.8571 3.4669 4.6844 1.5325
6.8705 3.4737 4.6935 1.5355
8.2889 4.1908 5.6624 1.8525
8.0362 4.0631 5.4898 1.7960
6.1296 3.0991 4.1874 1.3699
7.2934 3.6875 4.9824 1.6300
6.0996 3.0839 4.1669 1.3632
7.9784 4.0338 5.4503 1.7831
6.4408 3.2565 4.4000 1.4395
7.1839 3.6322 4.9076 1.6055
7.5153 3.7997 5.1340 1.6796
6.3744 3.2229 4.3546 1.4246
6.4136 3.2427 4.3813 1.4334
6.8334 3.4550 4.6682 1.5272
7.3559 3.7191 5.0251 1.6440
7.5652 3.8249 5.1681 1.6908
8.2609 4.1767 5.6433 1.8462
6.8460 3.4613 4.6768 1.5300
6.5086 3.2907 4.4463 1.4546
6.5188 3.2959 4.4533 1.4569
7.8420 3.9649 5.3571 1.7526
6.9860 3.5321 4.7724 1.5613
6.8426 3.4596 4.6745 1.5293
6.3186 3.1947 4.3165 1.4121
7.1241 3.6019 4.8667 1.5922
7.1261 3.6029 4.8681 1.5926
7.0336 3.5562 4.8049 1.5720
6.2484 3.1592 4.2685 1.3965
7.3141 3.6980 4.9965 1.6346
7.2343 3.6577 4.9420 1.6168
6.9308 3.5042 4.7347 1.5490
6.4349 3.2535 4.3959 1.4381
6.7801 3.4280 4.6318 1.5153
6.8399 3.4582 4.6726 1.5287
6.3778 3.2246 4.3569 1.4254