原文链接：https://blog.csdn.net/Coco_liukeke/article/details/72847264

一、前言

在推导出SVM公式的基础上，就可以考虑动手实现了。SVM解决分类问题，这里用MATLAB来实现，具体就不多说了，所以首先给出两种标记不同的点，然后分别标记为+1，-1。先训练，再测试，最后画图展示出来。代码也是主演参考的别人的，有加上自己的理解注释。

二、流程及实现

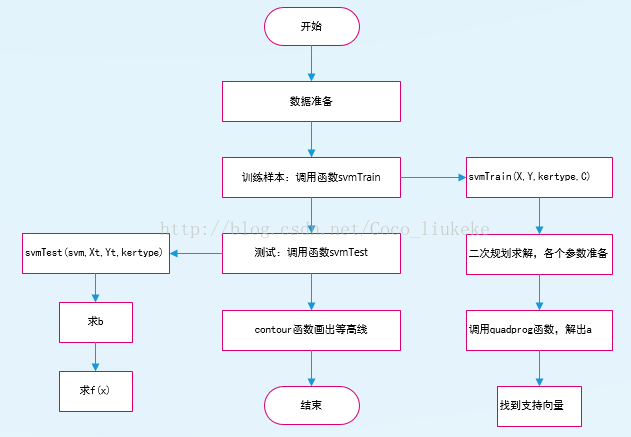
1.流程图

SVM自写代码 - 图1

2.大家对二次规划可能有点陌生，可以查看帮助文档或者百度，讲解得都很详细，下面是我简单记录一下，其实就是一一对应起来：

SVM自写代码 - 图2

3.得到大致流程之后，下面直接贴代码，复制之后就可直接运行。

主函数代码如下：

  1. %------------主函数----------------
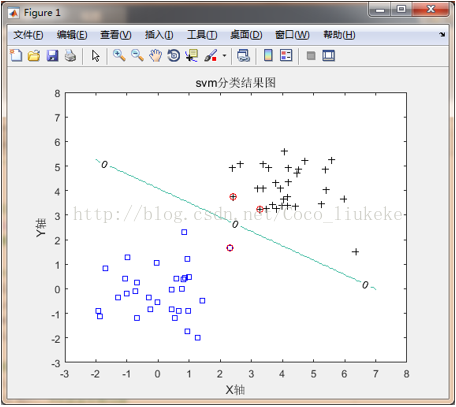
  2. clear all;
  3. close all;
  4. C = 10;  %成本约束参数
  5. kertype = 'linear';  %线性核
  7. %①------数据准备
  8. n = 30;
  9. %randn('state',6);   %指定状态，一般可以不用
  10. x1 = randn(2,n);    %2行N列矩阵，元素服从正态分布
  11. y1 = ones(1,n);       %1*N个1
  12. x2 = 4+randn(2,n);   %2*N矩阵，元素服从正态分布且均值为5，测试高斯核可x2 = 3+randn(2,n); 
  13. y2 = -ones(1,n);      %1*N个-1
  15. figure;  %创建一个用来显示图形输出的一个窗口对象
  16. plot(x1(1,:),x1(2,:),'bs',x2(1,:),x2(2,:),'k+');  %画图，两堆点
  17. axis([-3 8 -3 8]);  %设置坐标轴范围
  18. hold on;    %在同一个figure中画几幅图时，用此句
  20. %②-------------训练样本
  21. X = [x1,x2];        %训练样本2*n矩阵，n为样本个数，d为特征向量个数
  22. Y = [y1,y2];        %训练目标1*n矩阵，n为样本个数，值为+1或-1
  23. svm = svmTrain(X,Y,kertype,C);  %训练样本
  24. plot(svm.Xsv(1,:),svm.Xsv(2,:),'ro');   %把支持向量标出来
  26. %③-------------测试
  27. [x1,x2] = meshgrid(-2:0.05:7,-2:0.05:7);  %x1和x2都是181*181的矩阵
  28. [rows,cols] = size(x1);  
  29. nt = rows*cols;                  
  30. Xt = [reshape(x1,1,nt);reshape(x2,1,nt)];
  31. %前半句reshape(x1,1,nt)是将x1转成1*（181*181）的矩阵，所以xt是2*（181*181）的矩阵
  32. %reshape函数重新调整矩阵的行、列、维数
  33. Yt = ones(1,nt);
  35. result = svmTest(svm, Xt, Yt, kertype);
  37. %④--------------画曲线的等高线图
  38. Yd = reshape(result.Y,rows,cols);
  39. contour(x1,x2,Yd,[0,0],'ShowText','on');%画等高线
  40. title('svm分类结果图');   
  41. x1=xlabel('X轴');  
  42. x2=ylabel('Y轴');

训练样本函数svmTrain：

  1. %-----------训练样本的函数---------
  2. function svm = svmTrain(X,Y,kertype,C)
  3. % Options是用来控制算法的选项参数的向量，optimset无参时，创建一个选项结构所有字段为默认值的选项
  4. options = optimset;    
  5. options.LargeScale = 'off';%LargeScale指大规模搜索，off表示在规模搜索模式关闭
  6. options.Display = 'off';    %表示无输出
  7. %二次规划来求解问题，可输入命令help quadprog查看详情
  8. n = length(Y);  %返回Y最长维数
  9. H = (Y'*Y).*kernel(X,X,kertype);    
  10. f = -ones(n,1); %f为1*n个-1,f相当于Quadprog函数中的c
  11. A = [];
  12. b = [];
  13. Aeq = Y; %相当于Quadprog函数中的A1,b1
  14. beq = 0;
  15. lb = zeros(n,1); %相当于Quadprog函数中的LB，UB
  16. ub = C*ones(n,1);
  17. a0 = zeros(n,1);  % a0是解的初始近似值
  18. [a,fval,eXitflag,output,lambda]  = quadprog(H,f,A,b,Aeq,beq,lb,ub,a0,options);
  19. %a是输出变量，问题的解
  20. %fval是目标函数在解a处的值
  21. %eXitflag>0,则程序收敛于解x；=0则函数的计算达到了最大次数；<0则问题无可行解，或程序运行失败
  22. %output输出程序运行的某些信息
  23. %lambda为在解a处的值Lagrange乘子
  24. epsilon = 1e-8;  
  25. %0<a<a(max)则认为x为支持向量,find返回一个包含数组X中每个非零元素的线性索引的向量。
  26. sv_label = find(abs(a)>epsilon);    
  27. svm.a = a(sv_label);
  28. svm.Xsv = X(:,sv_label);
  29. svm.Ysv = Y(sv_label);
  30. svm.svnum = length(sv_label);
  31. %svm.label = sv_label;
  32. end

测试函数svmTest：

  1. %---------------测试的函数-------------
  2. function result = svmTest(svm, Xt, Yt, kertype)
  3. temp = (svm.a'.*svm.Ysv)*kernel(svm.Xsv,svm.Xsv,kertype);
  4. %total_b = svm.Ysv-temp;
  5. b = mean(svm.Ysv-temp);  %b取均值
  6. w = (svm.a'.*svm.Ysv)*kernel(svm.Xsv,Xt,kertype);
  7. result.score = w + b;
  8. Y = sign(w+b);  %f(x)
  9. result.Y = Y;
  10. result.accuracy = size(find(Y==Yt))/size(Yt);
  11. end

核函数kernel:

  1. %---------------核函数---------------
  2. function K = kernel(X,Y,type)
  3. %X 维数*个数
  4. switch type
  5. case 'linear'   %此时代表线性核
  6.   K = X'*Y;
  7. case 'rbf'      %此时代表高斯核
  8.   delta = 5;
  9.   delta = delta*delta;
  10.   XX = sum(X'.*X',2);%2表示将矩阵中的按行为单位进行求和
  11.   YY = sum(Y'.*Y',2);
  12.   XY = X'*Y;
  13.   K = abs(repmat(XX,[1 size(YY,1)]) + repmat(YY',[size(XX,1) 1]) - 2*XY);
  14.   K = exp(-K./delta);
  15. end
  16. end

4.结果

SVM自写代码 - 图3