这篇文章主要介绍什么？

本文的重点是展示我们选择最佳超平面的理由。
摘要：

• 我们如何找到最优的超平面？
• 我们如何计算两个超平面之间的距离？
• SVM优化问题是什么？

  如何找到最优超平面

  在上篇文章中，我们计算了一个点和一个超平面之间的距离,然后我们计算出间隔为。但是，即使在分离数据方面做得很好，它也不是最佳的超平面。
  
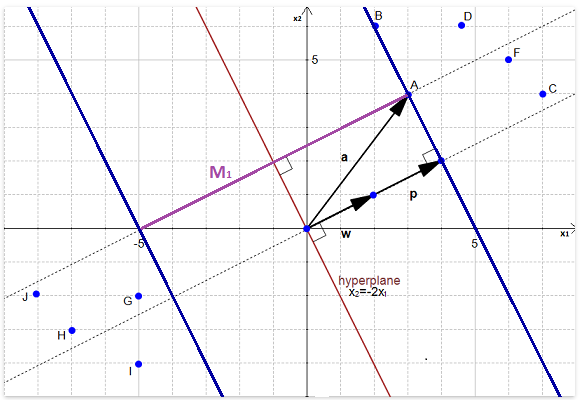
  正如我们在第一篇文章中讨论的那样，最佳超平面是使训练数据的间隔最大化的一种。在上图中，我们可以看到边距中有两条蓝线分割的，并不是将数据完美分开的最大余量。最大的间隔 是如下图所示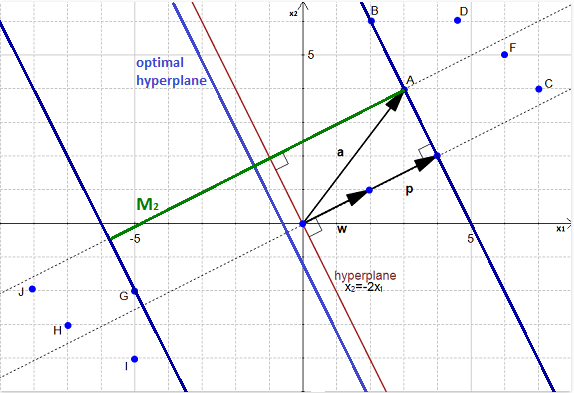
  
  这个超平面位于最初超平面的左侧，我们是怎么找到它的？我只是在两个超平面之间画了一个线段M这个时候我们应该感觉到超平面和边距紧密相关。你是对的！
  如果我有一个超平面，我可以计算出相对于某个数据点的间隔。如果我有一个由两个超平面界定的边距（图中的两条深蓝色线条），则可以找到第三个超平面在该边距的中间穿过。
  找到最大的间隔和找到最优的超平面是一回事。

  我们如何找到最大的间隔

  这很简单

1. 准备一个数据集
2. 选择两个将数据分开的超平面，他们之间没有点
3. 最大化他们的边距

由两个超平面界定的区域将是最大可能的边界。如果这么简单，为什么每个人都对SVM感到如此痛苦？这是因为与往常一样，简单性需要一些抽象和数学术语才能很好地理解。因此，我们现在要逐步地介绍下这份“食谱”：

Step1:有一个需要分类的数据集D

大多数情况下，数据是n维向量数据。每一个数据都都对应一个值。但是大部分情况下：例如做文本分类的情况下，向量最终有很多维度，如果它有P维时，我们称时一个P维向量。
所以数据集D 是一个n组元素的数据。更加通用的定义为：

Step2:选择两个分割数据的超平面，他们之间没有点

当有铅笔和纸时，找到两个分割数据的超平面很容易，但是P维大小的数据分割就很难，因为我们没有办法把它画出来。
而且，即使数据只是二维的，我们也可能找不到单独的超平面。
而且只有我们的数据是线性可分的，我们才能找到这样的一个超平面。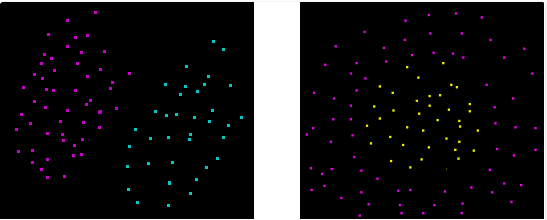

左边是线性可分的，右边的数据是线性不可分的。我们假设我们的数据是线性可分得，现在我们想要找到两个超平面，这两个超平面之间没有点。但是我们却没有方法去把他们可视化。
我们对可以帮助我们的超平面了解多少呢？

再看一下超平面方程

之前我们看到，超平面的方程可以写成：

当时，这个时候为三维数据，我们将他写成二维形式。,我们选择两个超平面和可以分割数据并且满足这样的式子：。因此得到和平面距离是相等的。
其实，变量并不是必要的，所以我们可以令来简化问题，所以得到了

现在我们想要确定他们之间是没有点的。我们并不是随便地选取的超平面，我们是要选择满足以下条件的超平面。
对于每一个，

理解下这个限制条件

在下面的这幅图中，所有的红色点是1这个类，所有的蓝色点是-1这个类。我们看下图中的A，它是红色的点，所以我们需要确认它与我们的限制条件不冲突。
当时，我们看到这个点在超平面上，这个条件就已经满足了。同样的情况，B也是满足的。当时，我们看到这个点位于超平面上，所以满足这个条件。同样的情况下，点D,E,F,G也满足了条件。
同样地，第二个限制条件也是被满足的。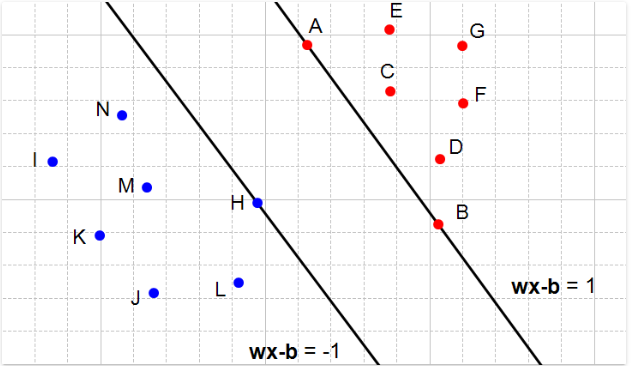

同样的下面这个图中的超平面也是满足条件的。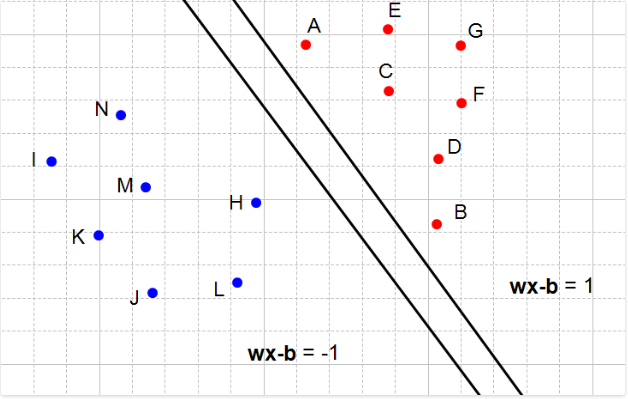

来看一下不满足条件的几种情况：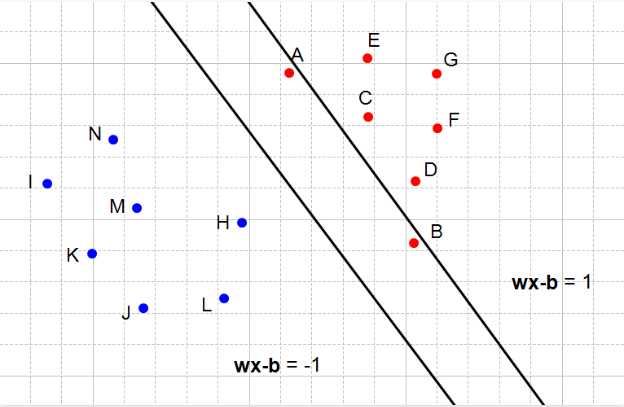

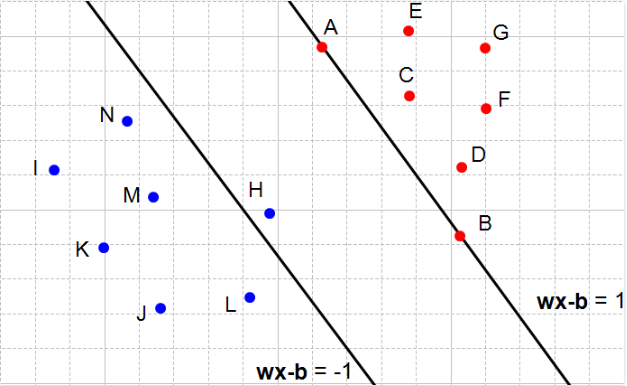
当限制条件不满足的时候意味着什么？它说明我们不能够选择这两个超平面，因为这两个超平面中间的都存在点。通过定义这些条件，我们就能够选择出中间没有点的超平面，这正面我们的需求。这种情况不仅仅适用于我们的例子中，而且也适用于p维条件下。

将两个式子联合起来

在 Mathematica中，人们总喜欢把事情能够简单地表示出来。上述的两个式子可以整合成一个式子。我们先来看第一个式子。我们知道它所归属的类为,所以我们在式子两边同乘以,注意要变号。

同理可以得到的条件。

所以这个式子就被整合成了一个式子

Step3:最大化两个超平面的距离

这个可能是问题中最难的一部分。但是不用担心，我们一步一步来解决这个问题。

a)两个超平面之间的距离是什么？

在我们想办法最大化两个超平面之间的距离的时候，我们首先要明白，我们怎么去计算这个距离？
首先：

• 这个超平面满足式子：
• 这个超平面满足式子：
• 是超平面中的点

我们把点到平面之间的垂直距离称为m。事实上，这个m就是我们叫做的间隔（margin）。因为在平面上，所以这个就是两个平面之间的距离。
我们现在要想办法求出这个距离。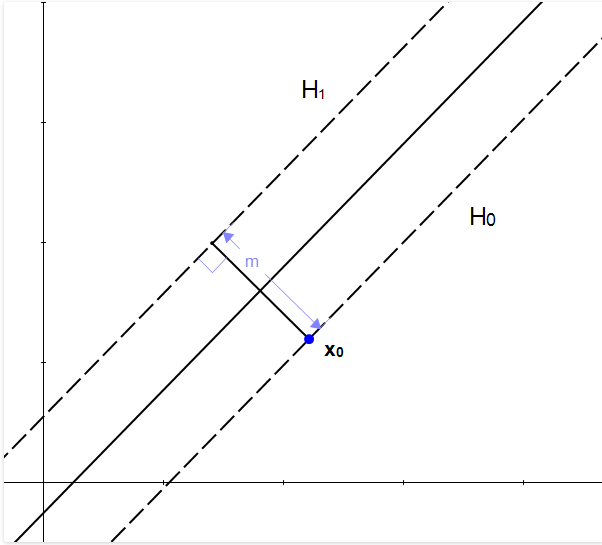

这个时候，你可能会想，如果我们在的基础上加上了一个的距离，我们可能会得到一个点，这个点并不在这个平面上，而是在其他平面上。
但是这个是行不通的。因为是一个标量，是一个向量，向量是不可能和标量相加的，所以我们要给规定一个方向，这样两个向量就能完成加法运算。
我们发现从开始的段距离的所有方向，最后成为了一个圆形：

从上图中我们可以发现仅仅只有距离是不够的，因为缺少了方向。我们不能直接用标量+向量，但是如果用标量×向量，我们就可以先把标量转换成一个向量。
从我们一开始的目标来看，我们想要的向量是：

• 长度为
• 与超平面是垂直的。

幸运的是，我们现在有一个现成的向量是垂直于的，这个向量就是,(因为)是不是也可以理解为叉积的形式。
通过向量我们可以定义上的单位向量：

这个向量的长度为1，方向与向量的相同。

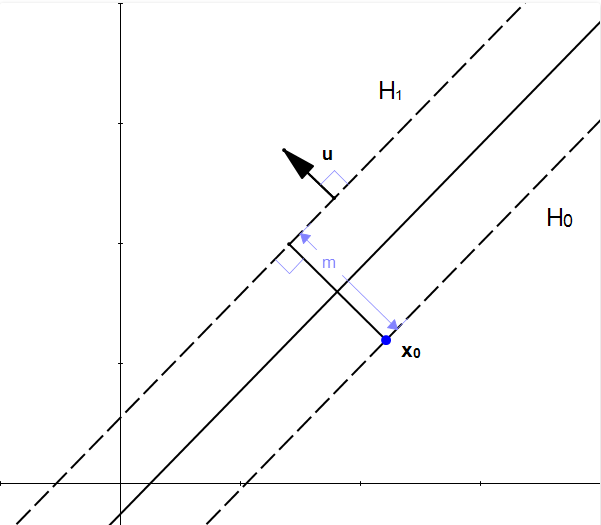
这个时候我们就得到了这个向量：,我们令这个向量

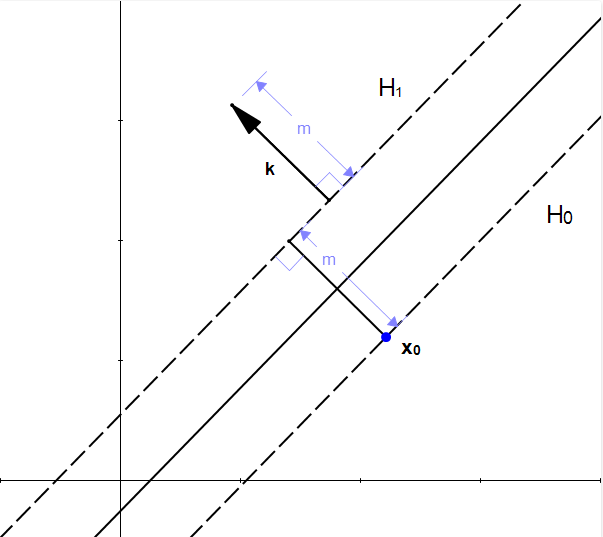
我们最终求出来了，我们找到了一个向量能够与向量相加，这个向量就是我们的向量，我们相加后的结果为向量

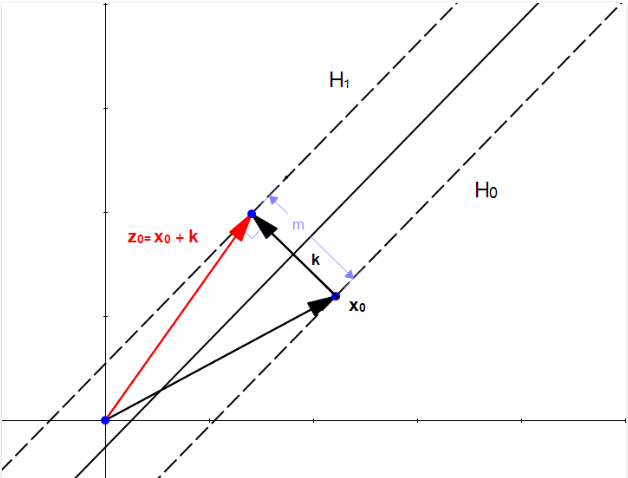
由于z位于超平面上，所以满足这个超平面方程：
接下来继续推导：

接下来我们逐推导：

因为我们的在平面上，所以，代入上述式子中，

经过上面一大堆的计算，我们最终算得了两个平面之间的距离

b)如何最大化两个超平面之间的距离

我们刚才得出了间隔大小：,我们想要最大化两个平面之间的距离，唯一能够改变的便是向量的长度。向量的长度越小，那么两个平面的间隔也就越大。

c)最大化超平面的间隔相当于最小化向量w的大小

由上面我们得到的条件：

解决我们的的关键就是解决上面的方程。所以我们的思路就是，在满足上面的方程的情况下，寻找出最小的。需要不断地迭代寻找。

结论

我们发现找到最佳超平面需要我们解决一个优化问题。优化问题本身有些棘手。您还需要更多背景信息才能解决这些问题。因此，我们将逐步进行。让我们在第4部分中发现无约束的最小化问题！谢谢阅读。