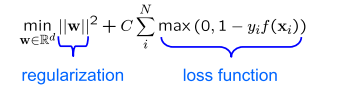硬间隔支持向量机的间隔计算为：
但是有时候将数据全部分开并不一定是最好的情况，有时候我们允许将一些数据进行错误的分类，这个我们需要对这个错误分类的点加上限制条件，不能让他错误分类的太厉害。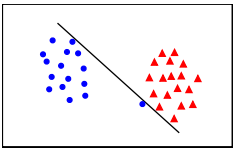
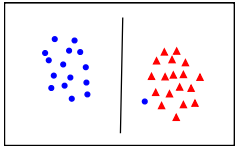
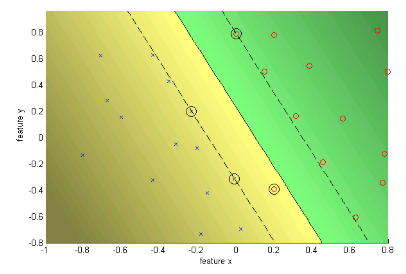
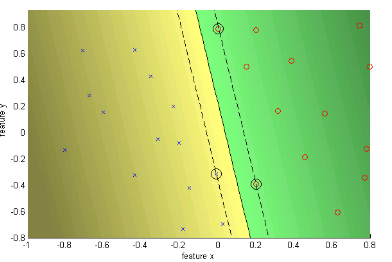
上图中的左面将两个数据全部分开，但是他们之间的间隔太小。这样的一个决策边界不能够很好地推广到那些看不见的数据。而图二，虽然没能够所有的数据完美分开，但是这样一个边界可以很好地用于推广。
软阈值的例子
从下面的图中，我们可以发现，中间的最佳超平面：
。两个间隔平面为：
。
- 两个间隔平面之间存在点的情况下，称之为软阈值间隔，它到超平面的间隔为
- 存在一个点在两个间隔平面之外，这个时候点要对应其对应的超平面，红色点对应红色超平面，其间隔
，这个时候我们称之为错误分类的点。
软阈值的优化
当超平面之间存在点的时候，我们的优化从硬间隔的
,变成了软间隔的优化公式：
目标函数：
能够足够大的情况下，我们上述的条件都能满足
时，这个条件就变成了硬间隔
只存在两种情况，
）和
,因为这个时候的点已经满足了分类条件)。
若有收获，就点个赞吧
0 人点赞
