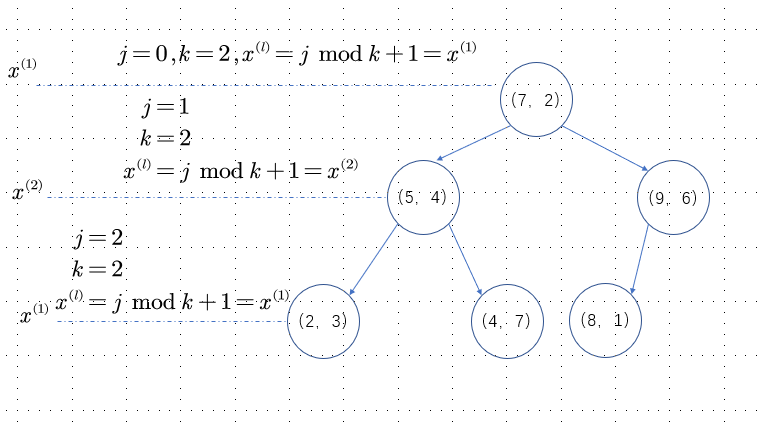
k-近邻简单来说，就是通过距离度量来选择最近的点：
例子：
已知二维空间的3个点，试求在取不同值时，距离下的最近邻点。（关于范数的讲解）
解：

• 因为和只有第一维的值不同，所以为任何值时，；
• 

所以我们可以得到，当时，，最近邻点为；当时，，最近邻点为

k值的选择

当较小时，相当于用较小的邻域中的训练实例进行预测，”学习”近似误差会减小，只有与输入实例相似的训练实例才会对预测结果起作用。但是，”学习”的估计误差会增大，预测结果会对近邻的实例点非常敏感，如果邻近的实例点是噪声，预测就会出错。
k值减小意味着整体模型变得复杂，容易过拟合；
当较大时，相当于用较大邻域中的训练实例进行预测。可以减少学习的估计误差，但是学习的近似误差会增大。这时与输入实例较远的（不相似）训练误差也会对预测起作用，使预测发生错误。

分类决策规则

在选取的个点中，按照各类点数的大小进行分类。

构造平衡kd树

算法描述

输入：维空间数据集，其中其中，
输出：树
（1）开始：构造根节点，根节点对应于包含T的k维空间的超矩形区域。
选择为坐标轴，以T中所有实例的坐标的中位数为切分点，将根节点对应的超矩形区域切分为两个子区域。切分由通过切分点并与坐标轴垂直的超平面实现。
由根节点生成深度为1的左、右子节点：左子节点对应坐标小于切分点的子区域，右子节点对应于坐标大于切分点的子区域。
将落在切分超平面上的实例点保存在根节点。
（2）重复：对深度为的节点，选择为切分的坐标轴，，以该节点的区域中所有实例的坐标的中位数为切分点，将该节点对应的超矩形区域切分为两个子区域。切分由通过切分点并与坐标轴垂直的超平面实现。
由该节点生成深度为左、右子节点：左子节点对应坐标小于切分点的子区域，右子节点对应坐标大于切分点的子区域。
将落在切分超平面上的实例点保存在该节点。
（3）直到两个子区域没有实例存在时停止，从而形成树的区域划分。

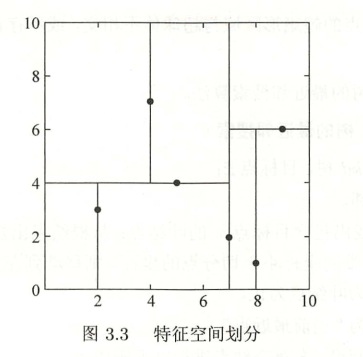
例子

给定一个二维空间的数据集：

构造一个平衡树。

最近邻搜索

算法描述

输入：已构造的树，目标点
输出：的最近邻。
（1）在树中找出包含目标点的叶节点：从根节点出发，递归地向下访问树。若目标点当前维的坐标小于切分点的坐标，则移动到左子节点，否则移动到右子节点。直到子节点为叶节点为止。
（2）以此叶节点为”当前最近点”。
（3）递归地向上回退，在每个节点进行以下操作
（a）如果该节点保存的实例比当前最近点距离目标点更近，则以该实例点为”当前最近点”
（b）当前最近点一定存在于该节点一个子节点对应的区域，检查该子节点的父节点的另一子节点对应的区域是否有更近的点。具体地，检查另一子节点对应的区域是否以目标点位球心、以目标点与”当前最近点”间的距离为半径的超球体相交。
如果相交，可能存在另一个子节点对应的区域内存在距目标点更近的点，移动到另一个子节点，接着，递归地进行最近邻搜索；
如果不相交，向上退回
（4）当退回到根节点时，搜索结束。最后的”当前最近点”即为的最近邻点。

例题

给定一个如图3.5所示的树，根节点为A，其子节点为B，C等。树上共存储7个实例点；另有一个输入目标实例点S，求S的最近邻。

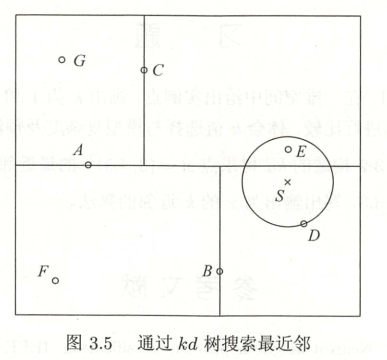
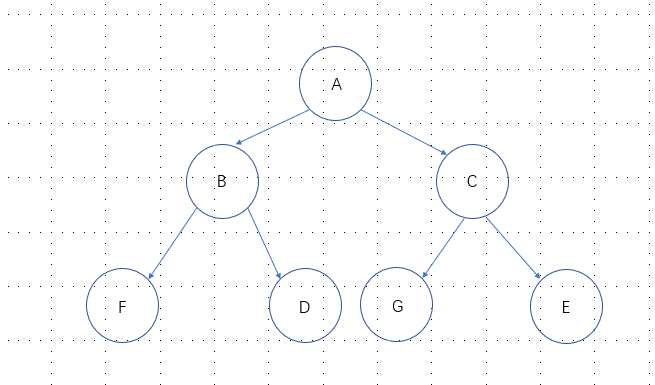
解：
首先在树种找到包含点S的叶节点D（即图中点S在点D所在的长方形种）（图中的右下区域），以点D作为近似最近邻。真正最近邻一定在以S为中心通过点D的圆的内部。
然后返回节点D的父节点B，在节点B的另一子节点F的区域内搜索最近邻。节点F的区域与圆不相交，不可能有最近邻点。
即需返回上一级父节点A，在节点A的另一子节点C的区域内搜索最近邻。节点C的区域与园相交；该区域在圆内的实例点有点E，点E比点D更近，称为新的最近邻近似。得到点E是点S的最近邻。