13.1未标记样本

图一
这样通过与外界的交互来将部分未标记样本转变为有标记样本，如果不与这些未标记的瓜进行交互，得不到它们的信息，还能否利用未标记样本来提高泛化性能吗？
答案是”Yes”。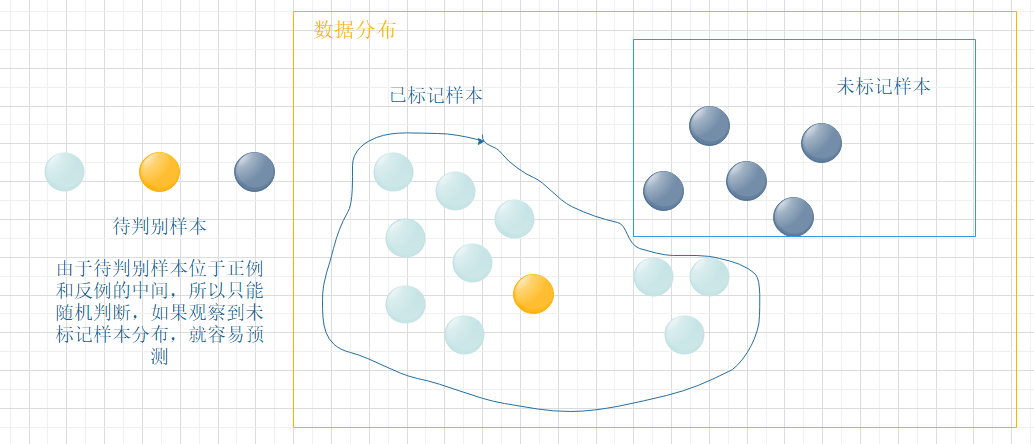

图二
让学习器不依赖外界交互、自动地利用未标记样本来提升学习性能，就是半监督学习（semi-supervised learning）。在现实应用中容易收集到大量未标记样本，而获取”标记”非常耗力，半监督学习就提供了一条简单的途径。
利用未标记样本的方法：

• 1.簇类假设，如上图二所示，假设数据存在簇结构，同一个簇的样本属于同一个类别。
• 2.流形假设，假设数据分布在一个流形结构上，邻近的样本拥有相似的输出值，流形假设是聚类假设的推广，但流形假设对输出值没有限制，比聚类假设的适用范围更广。（聚类假设考虑的是类别标记，通常用于分类任务）
• 3.聚类假设和流形假设的本质是”相似的样本拥有相似的输出”。

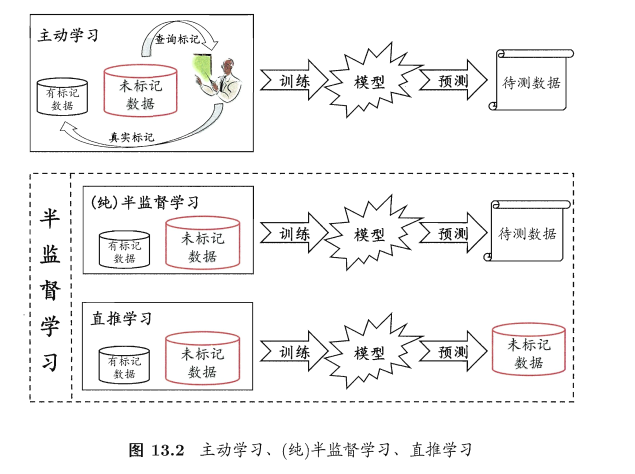
  13.2 生成式方法

  
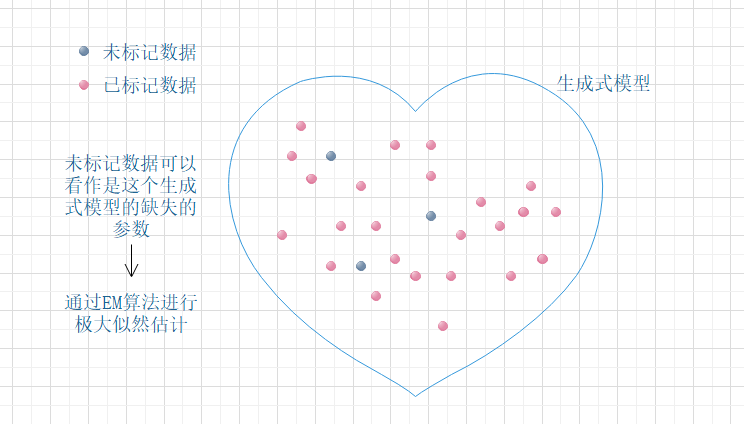
  给定样本，其真实类别标记为，其中为所有可能的类别，假设样本由高斯混合模型生成，且每个类别对应一个高斯混合成分。换言之，数据样本是基于如下概率密度生成：
  

  解析:高斯混合分布的定义式.

其中，混合系数是样本属于第个高斯混合成分的概率；和为该高斯混合成分的参数。
令表示模型对的预测标记，表示样本隶属的高斯混合成分。由最大化后验概率可知

解析:从公式第1行到第2行是对概率进行边缘化(marginalization);通过引入并对其求和以抵消引入的影响.从公式第2行到第3行推导如下:

其中

解析:根据13.1 因此

为样本由第个高斯混合成分生成的后验概率，为由第个高斯混合成分生成且其类别为的概率。由于假设每个类别对应一个高斯混合成分，因此仅与样本所属的高斯混合成分有关，可用代替，不失一般性，假定第个类别对应于第个高斯混合成分，即当且仅当，否则.
不难发现,式子(13.2)中估计需知道样本的标记,因此仅能使用标记数据;而不涉及样本标记,因此有标记和未标记数据均可利用,通过引入大量的未标记数据,对这一项的估计可望由于数据量的增长更为准确,于是式子(13.2)整体的估计可能会更准确,由此可清楚地看出未标记数据为什么能提高分类模型的性能?
给定标记样本集和
未标记样本集.假设所有样本独立同分布,且都是由同一个高斯混合模型生成的,用极大似然法来估计高斯混合模型的参数的对数似然是

解析:第二项很好解释,当不知道类别信息的时候,样本的概率可以用式子(13.1)表示,所有无类别信息的样本的似然是所有样本的乘积,因为函数是单调的,所以也可以将函数作用域这个乘积消除因为连乘产生的数值计算问题,第一项引入了样本的标签信息,由 可知,这项限定了样本只可能来自于来自所对应的高斯分布.

式子(13.4)由两项组成:基于有标记数据的有监督项和基于未标记数据的无监督项.显然,高斯混合模型参数估计可用EM算法求解,迭代更新式如下:

• E步:根据当前模型参数计算未标记样本属于高斯混合成分的概率

解析:参见式子13.3,这项可以理解成样本属于类别标签(或者说由第个高斯分布生成)的后验概率.其中可以通过有标记样本预先计算出来.即:

• M步:基于更新模型参数,其中表示第类的有标记样本数目

推导：这项可以由

而得，而将13.4的两项分别记为： 首先，对求偏导，求和号中只有的项能留下来，即 对求导，参考9.33的推导： 综上， 令，两边同时左乘并移项： 上式中，可以作为常量提到求和号外面，而，即第类样本的有标记样本数目，因此： 即得式子13.6

推导：类似于13.6由得，化简过程同13.6过程类似首先对求偏导，类似于13.6 然后对求偏导，类似于式子9.35 综合可得： 令，两边同时右乘并移项： 两边同时左乘: 即可得13.7

推导：类似式子9.36，写出得拉格朗日形式 类似于式子9.37，对求偏导。对于，求导结果与式子9.37的推导过程一样 对于，类似于式子13.6和13.7的推导过程： 上式推导过程中，重点注意变量是是常量；最后一行相对于求和变量为常量，因此作为公因子提到求和号外面，为第类样本的有标记样本数目，综合两项结果： 令并且两边同乘以，得 结合式子9.30发现，求和号内即为后验概率，即 对所有混合成分求和，得 这里，因此，根据9.30中表达式可知 再结合加法满足交换律，所以 以上分析过程中，形式与等价，其中为未标记样本集得样本个数；其中为有标记样本集的样本个数；将这些结果代入 解出且其中为样本总个数，移项即得最后带入整理解得 整理即得13.8

以上过程不断迭代直至收敛,即可获得模型参数,然后由式子(13.3)和(13.2)就能对样本进行分类.
将上述过程中的高斯混合模型换成混合专家模型,朴素贝叶斯模型等即可推导出其他的生成式半监督学习方法,在有标记数据极少的情况下往往比其他方法性能更好.这个方法有一个关键:模型假设必须准确,即假设的生成式模型必须与真实数据分布吻合;否则利用未标记数据会降低泛化性能.

13.3 半监督SVM

不考虑未标记样本时，支持向量机试图找到最大间隔划分超平面；
考虑未标记样本时，S3VM试图找到能将两类标记样本分开，且穿过数据低密度区域的划分超平面，如图13.3所示，这里的基本假设是”低密度分隔”（low-density separation）。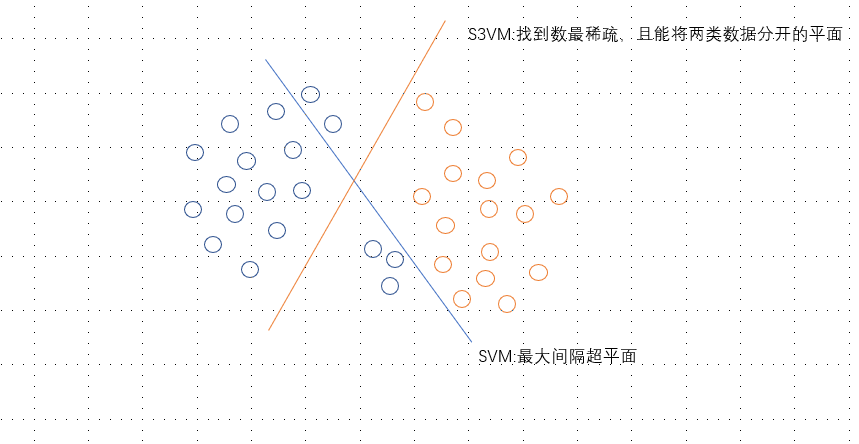

图13.3
半监督支持向量机中最著名的是TSVM(Transuctive Support Vector)，是针对二分类问题的学习方法。TSVM试图考虑对未标记样本进行各种可能的标记指派（label assignment），即尝试将每个未标记样本分别作为正例或反例，然后在所有这些结果中，寻求一个所有样本（包括有标记样本和进行了标记指派的未标记样本）上间隔最大化的划分超平面，一旦超平面确定，未标记样本的标记指派就是其预测结果。
给定和，其中,，TSVM的目标是为中的样本给出预测标记，使得

解析：这个公式和公式6.35基本一致，除了引入了无标记样本的松弛变量和对应的权重系数和无标记样本的标记指派。

其中，确定了一个划分超平面，为松弛向量，对应于有标记样本，对应于未标记样本，是由用户指定的用于平衡模型复杂度、有标记样本与未标记样本重要程度的折中参数。
标记指派未标记样本是一个穷举过程，当未标记样本很少的时候才可能直接求解，这时需考虑更高效的优化策略。

在对未标记样本进行标记指派及调整的过程中，有可能出现类别不平衡问题，即某类的样本远多于另一类，这将对SVM的训练造成困扰，为了减轻不平衡性带来的不利隐形，对图13.4的算法稍加改进；将优化目标中的拆分为与两项，分别对应基于伪标记而当作正、反例使用的未标记样本，并在初始化时令

其中与为基于伪标记而当作正、反例使用的未标记样本数。
在图13.4算法的第6—10行中，若存在一对未标记样本与，其标记指派与不同，且对应的松弛变量满足，则意味着与很可能是错误的，需对二者进行交换后重新求解式子（13.9），这样每轮迭代后均可使式子（13.9）的目标函数值下降。
搜寻标记指派可能出错的每一对未标记样本进行调整，是一个涉及巨大计算开销的大规模优化问题，因此，半监督SVM研究的一个重点是如何设计出高效的优化求解策略