基本概念

学习类型

监督学习

监督学习是指从有标注的数据中学习模型；比如：回归模型（简单线性回归，多元线性回归），分类模型（逻辑斯蒂回归，决策树）

有标注是什么意思？自变量和因变量同时存在的，因变量就可以理解为标注

无监督学习

无监督学习是指从没有标注的数据中学习模型；比如：聚类、降纬

无标注是什么意思？就是只有自变量，没有因变量，数据集中只包含输入部分，没有输出部分，需要自我挖掘，自我驱动

半监督学习

半监督学习是指从部分有标注，部分没标注的数据中学习模型

聚类概述

聚类是针对给定的样本，依据它们的特征的相似度或距离，将其归并到若干个“类”或“簇”的数据分析问题。一个类是给定样本集合的一个子集。

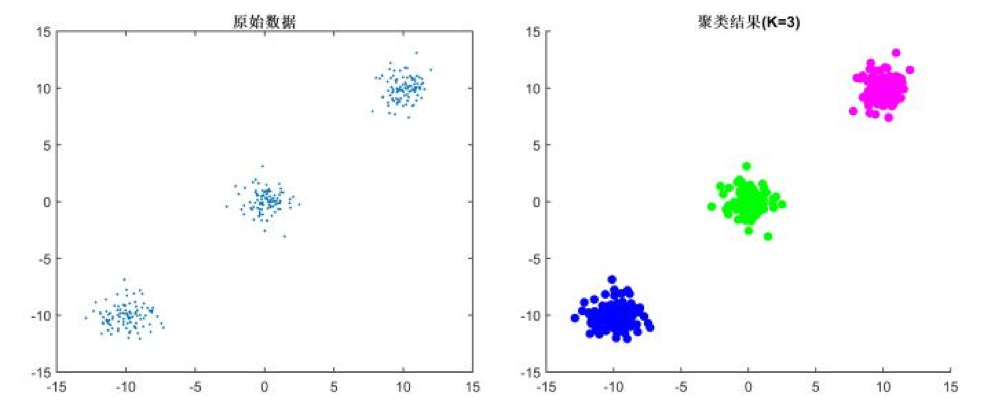
聚类概述.png

聚类的关键性动作就是：分类

如何分类？通过计算样本间的相似度（距离）

聚类案例

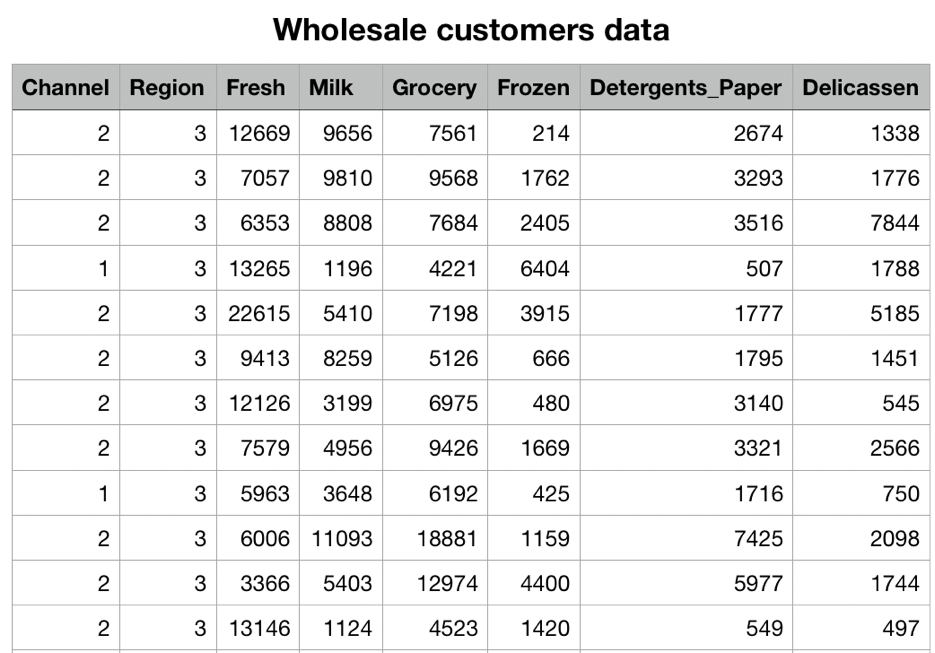
聚类案例.png

  • Wholesale的案例数据表明了其消费者对不同类别商品的年度消费金额；
  • 目标是根据消费记录客户进行类别划分

距离计算

闵可夫斯基距离

闵可夫斯基距离.png

解释一下什么是m维实数向量？看下面的图

每一行表示是一个样本，每一列表示是一个特征。共有m个特征，也可看作是m维实数向量。

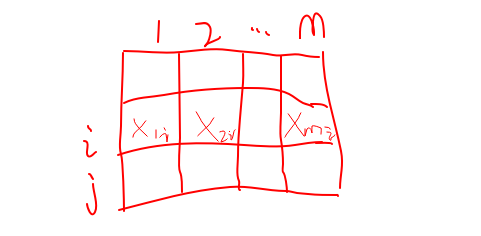
闵可夫斯基解释.png

为什么说距离越大相似度越小？

我们看，欧式距离不就是计算平面上两个点之间的距离吗？距离越远，表示两个点的相异性越大（即相似度小），距离越近，表示两个点的相异性越小（即相似度达）

马哈拉诺比斯距离

马氏距离.png

与各个特征的尺度无关是啥意思？看下面的图

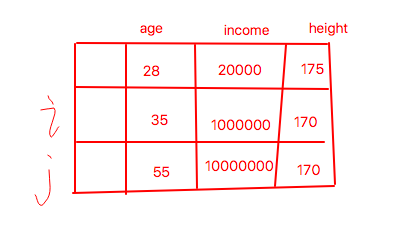
马氏距离解释.png

我们有3个特征，age范围在0到100之间，height范围假设在0到200之间，但income收入却是一个没有上限的值。

如果我们用欧式距离计算样本 i 和样本 j 的相似程度

那么income这个特征会导致计算结果很大，因为计算里包含着1000万减100万的平方

简单点说：就是income这个特征的度量尺度相对其它特征太大了

而马氏距离的计算可以帮助我们避免这个问题（因为计算中包含了协方差距离）

公式剖析

两个样本之间的距离distance计算，公式中使用中括号包裹，是表示里面是矩阵计算的意思

左边是一个行向量的转置，最终为列矩阵的形式；中间为协方差矩阵的逆；右边为行向量；最终的计算结果开平方

相关系数

样本之间的相似度使用相关系数来表示。相关系数的值越接近1，表示样本越相似；越接近0，表示样本越不相似。

相关系数.png

余弦距离

样本之间的夹角余弦来表示余弦距离。夹角余弦的值越接近1，表示样本越相似；越接近0，表示样本越不相似。

余弦距离.png

公式中分子是样本间各个特征相乘然后累加，分母是每个样本特征的平方和相乘开根号

看图理解

余弦距离解释.png

结语

具体选用哪种距离来衡量？取决于数据本身适合使用哪类距离以及自身对业务的理解程度。

KMeans算法

精简版算法描述

K均值聚类的两步骤：

  1. 选择k个类的中心，将样本逐个指派与其最近的中心类中，得到一个聚类结果
  2. 更新每个类的样本均值，作为类的新的中心

重复以上步骤，直到收敛为止。

详细解释：选择k个类的中心；其实做了两个动作，动作一：主观选择最终要聚合成几个类，即k值定为多少、动作二：分别选取k个类的中心点，通过随机选取样本的方式。（比方说，我们根据业务需要设定k值为3，那我们随机选取3条样本分别作为3个类别的中心点）

详细解释：逐个指派；假设我们有n条样本，m个特征，k值为3，那我们针对每个样本分别计算与3个类别中心点的距离（上面我们介绍的距离计算方式），把该样本丢入距离最小的类别中，总共有3n次计算，这样便得到了一个聚类结果

详细解释：更新每个类的样本均值；很明显，我们第一次计算选取中心点是随机的，这样的聚类结果不是最优的，那我们怎么进行更新呢？计算每个类中的样本均值，即对该类别中所有样本的每个特征求平均数，将该样本均值作为类新的中心

详细解释：直到收敛；收敛是什么意思？随着迭代次数的增加，各个类别里的样本不再发生变化，即称之为收敛。或者变化的幅度在我们允许的范围内

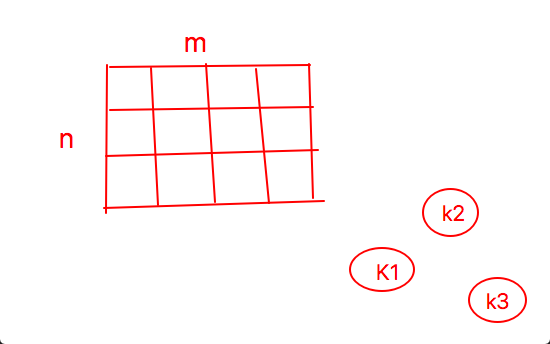
聚类算法图解.png

严谨版算法描述

聚类算法.png

第一个红线解释；上标表示 t，即迭代次数；下标表示类别，共选取了 k 个类

第二个红线解释；我们是怎么计算新的类中心的，通过计算均值（mean），这也是为什么叫k-means的缘故，k表示类别数，mean求平均

聚类过程

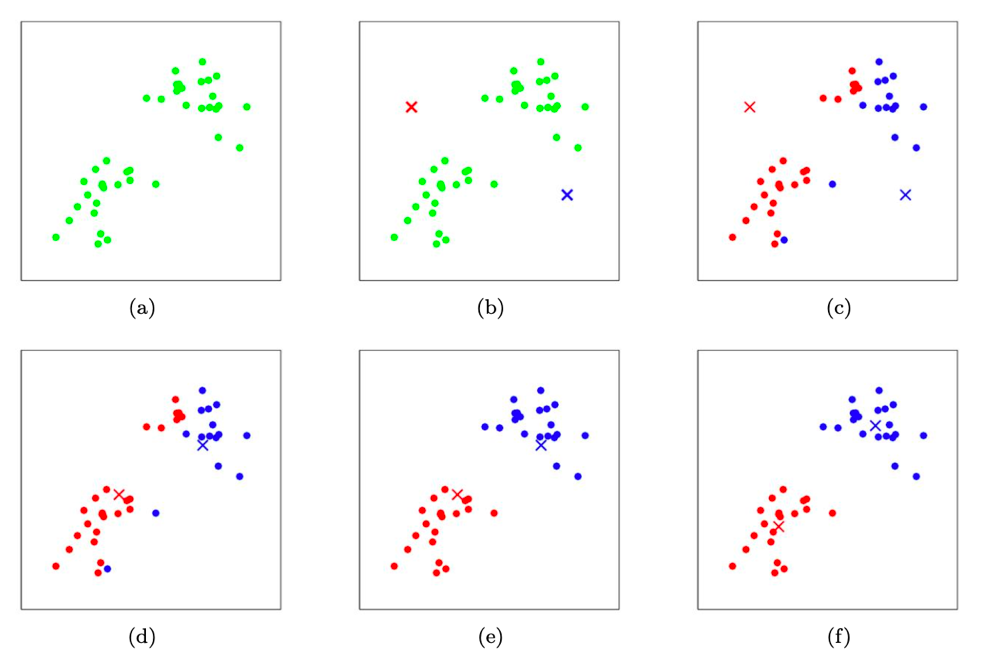
聚类过程.png

初始化

  1. 原始数据集（对应子图a）
  2. 随机初始化聚类中心（对应子图b）(通常我们是随机选取样本作为初始聚类中心，这里是随机初始化也可以)

样本聚类

  1. 样本进行类别分配（对应子图c）
  2. 重新计算聚类中心（对应子图d）
  3. 重新进行样类别分配（对应子图e）

聚类模型

  1. 两次迭代，最终聚类结束，形成两个类（对应子图f）

KMeans优缺点

优点:

  1. 原理比较简单，实现也是很容易，收敛速度快。
  2. 当结果簇是密集的，而簇与簇之间区别明显时, 它的效果较好。
  3. 主要需要调参的参数仅仅是簇数k。

关于第二点也就是说，数据集中有明显的隔离带，这就表明结果簇是密集的（同一个簇内的数据集是聚集在一块的），并且簇与簇之间区别明显（簇与簇之间的距离足够远）。所以可能针对较为分散的数据集，kmeans算法的表现就没那么好了。

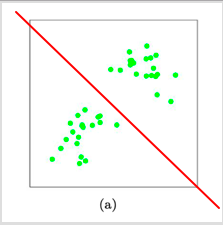
  1.                                     ![优点2.png](https://cdn.nlark.com/yuque/0/2020/png/706453/1581392106791-fb5298ba-bae4-44eb-a1aa-e011fff0425c.png#align=left&display=inline&height=225&margin=%5Bobject%20Object%5D&name=%E4%BC%98%E7%82%B92.png&originHeight=225&originWidth=223&size=13241&status=done&style=none&width=223)

缺点:

  1. K值需要预先给定，很多情况下K值的估计是非常困难的。
  2. K-Means算法对初始选取的质心点是敏感的，不同的随机种子点得到的聚类结果完全不同 ，对结果影响很大。
  3. 对噪音和异常点比较敏感。也就是说异常点会导致kmeans算法的效果变差。
  4. 采用迭代方法，可能只能得到局部的最优解，而无法得到全局的最优解。

面试常考

  • 口述k-means算法的过程
  • 口述k-means算法的优缺点
  • 用笔推导k-means算法（进阶）
  • 手写代码实现k-means算法（数据挖掘）

代码实现

加载模块

  1. import numpy as np
  2. import pandas as pd
  3. import matplotlib.pyplot as plt
  4. import seaborn as sns
  6. from mpl_toolkits.mplot3d import Axes3D
  7. from sklearn.cluster import KMeans
  8. from sklearn import datasets

加载鸢尾花数据

  1. iris = datasets.load_iris()
  2. X = iris.data
  3. Y = iris.target
  4. print(iris.feature_names)

执行

  1. ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']

这里稍微说明一下：X 是150行4列的二维数组；Y是因变量指定类别，后面我们把预测结果和真实结果作对比用

训练模型

  1. cluster = KMeans(n_clusters=3)
  2. cluster.fit(X)

执行

  1. KMeans(algorithm='auto', copy_x=True, init='k-means++', max_iter=300,
  2.        n_clusters=3, n_init=10, n_jobs=None, precompute_distances='auto',
  3.        random_state=None, tol=0.0001, verbose=0)

输出的结果是Kmeans模型中我们指定的参数值以及默认的参数

进行预测

  1. y_pred = cluster.predict(X)
  2. y_pred

执行

  1. array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
  2.        0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
  3.        0, 0, 0, 0, 0, 0, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
  4.        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
  5.        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 2, 2, 2, 2, 1, 2, 2, 2,
  6.        2, 2, 2, 1, 1, 2, 2, 2, 2, 1, 2, 1, 2, 1, 2, 2, 1, 1, 2, 2, 2, 2,
  7.        2, 1, 2, 2, 2, 2, 1, 2, 2, 2, 1, 2, 2, 2, 1, 2, 2, 1], dtype=int32)

作对比

我们把预测结果和真实数据作一个对比，看一看预测的正确率有多少？

  1. df = pd.DataFrame(Y, columns=['init']) 
  2. df['pred'] = y_pred
  3. df

执行

init pred
0 0 0
1 0 0
2 0 0
3 0 0
4 0 0
… … …
145 2 2
146 2 1
147 2 2
148 2 2
149 2 1

150 rows × 2 columns

看一下有多少预测值和真实值是不同的

  1. len(df[df['init'] != df['pred']])                   # 16
  3. 16 / 150                                        # 0.10666666666666667

我们可以看到在预测的结果中，将近90%的正确率了

不同的聚类模型对比

三个聚类模型

我们之前讲初始情况下选取不同的质心点会导致最终形成的聚类结果不同，Kmeans中的 n_init 默认值为10，也就是选取10次，而在第三个聚类模型中，我们设置n_init值为1，也就是只运行一次

  1. # 构建三个不同的聚类模型
  2. estimators = [('k_means_iris_8', KMeans(n_clusters=8)),
  3.               ('k_means_iris_3', KMeans(n_clusters=3)),
  4.               ('k_means_iris_bad_init', KMeans(n_clusters=8, n_init=1, init='random'))]
  5. titles = ['8 clusters', '3 clusters', '3 clusters, bad initialization']

通过3D可视化的方式，将聚类的结果展现出来

fignum = 1
for name, est in estimators:
    # 创建一个画布
    fig = plt.figure(fignum, figsize=(5, 4))
    ax = Axes3D(fig, rect=[0, 0, .95, 1], elev=48, azim=134)
    est.fit(X)
    # 等同于预测的值y_pred
    labels = est.labels_

    # 散点图展示
    ax.scatter(X[:, 3], X[:, 0], X[:, 2], c=labels.astype(np.float), edgecolor='k')

    # 设置轴上的刻度标记为空
    ax.w_xaxis.set_ticklabels([])
    ax.w_yaxis.set_ticklabels([])
    ax.w_zaxis.set_ticklabels([])
    # 设置对应轴上的label
    ax.set_xlabel('Petal width')
    ax.set_ylabel('Sepal length')
    ax.set_zlabel('Petal length')

    # 设置该图片的title
    ax.set_title(titles[fignum - 1])
    # 和图片的大小有关
    ax.dist = 12
    fignum = fignum + 1

0.png
1.png
2.png

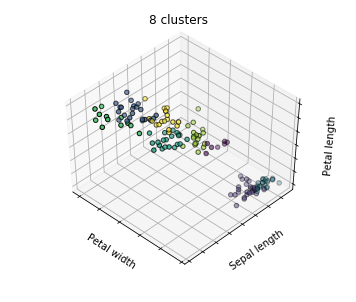
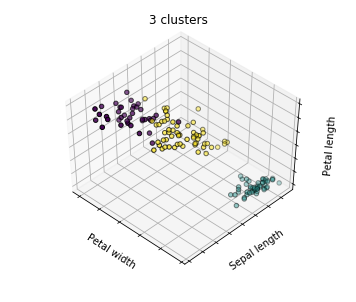
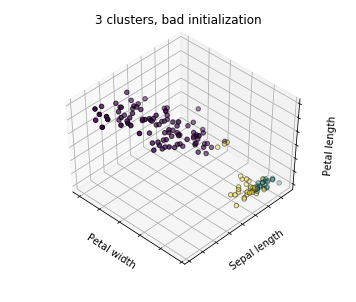
看图说话

  • 第一个子图，类别太多，有点杂乱无章，也就是类与类之间不够泾渭分明
  • 第二个子图，相对较好的结果，其中一个类和另外两个类有明显的分隔带
  • 第三个子图，bad case，虽然最终结果也是3个类别

真实数据

fig = plt.figure(fignum, figsize=(5,4))
# elev和azim参数是用来设置角度的
ax = Axes3D(fig, rect=[0, 0, .95, 1], elev=48, azim=134)

for name, label in [('Setosa', 0),
                    ('Versicolour', 1),
                    ('Virginica', 2)]:
    ax.text3D(X[Y == label, 3].mean(),
             X[Y == label, 0].mean(),
             X[Y == label, 2].mean() + 2,
             name,
             horizontalalignment = 'center',
             bbox = dict(alpha=.2, edgecolor='w', facecolor='w'))

# Reorder the labels to have colors matching the cluster results
Y = iris.target
Y = np.choose(Y, [1, 2, 0]).astype(np.float)
ax.scatter(X[:, 3], X[:, 0], X[:, 2], c=Y, edgecolor='k')

ax.w_xaxis.set_ticklabels([])
ax.w_yaxis.set_ticklabels([])
ax.w_zaxis.set_ticklabels([])
ax.set_xlabel('Petal width')
ax.set_ylabel('Sepal length')
ax.set_zlabel('Petal length')

ax.set_title('Ground Truth')
ax.dist = 12

4.png

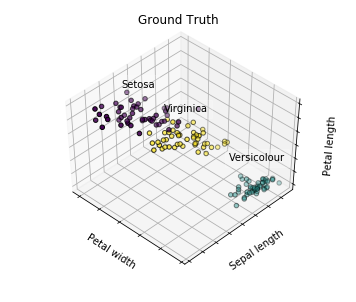
我们可以明显看到，该图（真实数据）与上面预测结果中的第二个子图较为相似。