第一题 递延所得税

Sparr 投资有限公司专门为其顾客研究如何投资，从而能够延缓投资的纳税机会。最近，Sparr 为某公司员工提供了一项工资单扣减投资计划。Sparr 估计目前该公司员工平均每月可延缓纳税的投资额不超过 100 美元。Sparr 根据一个由 40 名员工组成的样本，对目前员工总体投资活动的水平进行假设检验。假定职员每月可延缓纳税的投资额的标准差为 75 美元，假设检验中取显著性水平 为 0.05。

  1. 在这种情况下，发生第二类错误意味着什么?
  2. 当员工每月实际投资的均值为 120 美元时发生第二类错误的概率为多大?
  3. 当员工每月实际投资的均值为 130 美元时发生第二类错误的概率为多大?
  4. 假定样本容量为 80 名员工，重复(2)和(3)中的问题。

第一问

建立假设：
假设检验习题 - 图1 假设检验习题 - 图2
**
显著性水平：0.05

第二类错误即：原假设为假却接受了原假设，即我们认为每月可延缓纳税的的投资额是小于等于100美元的，但实际上却是大于100美元的。

第二问

检验统计量：假设检验习题 - 图3

  1. from scipy.stats import norm
  2. import numpy as np
  4. # 上侧检验
  5. zmin = abs(norm.ppf(0.05)) * 75 / np.sqrt(40) + 100
  6. print(zmin)          # 119.5

即如果抽样样本的均值是大于等于119.5，我们则甘愿冒着风险拒绝原假设。求解第二类错误的概率，即假定总体均值是大于100的，同时计算样本均值小于119.5的概率。

  1. z = (zmin - 120) / 75 * np.sqrt(40)
  3. # 直接对应的就是左侧面积
  4. p = norm.cdf(z)
  5. print(p)            # 0.483

即当总体均值为120美元时，发生第二类错误的概率为48.3%。

第三问

  1. z = (zmin - 130) / 75 * np.sqrt(40)
  3. p = norm.cdf(z)
  4. print(p)           # 0.188

即当总体均值为130美元时，发生第二类错误的概率为18.8%。

第四问

  1. zmin = abs(norm.ppf(0.05)) * 75 / np.sqrt(80) + 100
  2. print(zmin)             # 即如果抽样样本的均值是大于113.8，则我们甘愿冒着风险拒绝原假设
  4. z = (zmin - 120) / 75 * np.sqrt(80)
  5. p = norm.cdf(z)
  6. print(p)                # 当总体均值为120美元时，发生第二类错误的概率为23%
  8. z = (zmin - 130) / 75 * np.sqrt(80)
  9. p = norm.cdf(z)
  10. print(p)                # 当总体均值为130美元时，发生第二类错误的概率为2.66%

执行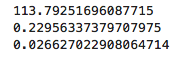
image.png
可以很明显的看到，当抽样的样本容量变大后，显著性水平不变的情况，发生第二类错误的概率变小了。

第二题 可口可乐

据可乐可口公司报道(可口可乐公司官网，2009 年 2 月 3 日)，美国年人均饮料销售量为 423 瓶。可乐可口总部位于美国佐治亚州亚特兰大，假如你想知道在亚特兰大可口可乐饮料的销售量是否更高。由来自亚特兰大地区的 36 人组成的一个样本显示，年销售量的样本均值为 460.4 瓶，标准差 s=101.9。取 a=0.05,样本结果是否支持得出结论认为可乐可口饮料在亚特兰大的年平均销售量更高?

解答：
建立假设：
假设检验习题 - 图5 假设检验习题 - 图6

显著性水平：0.05

计算检验统计量：**假设检验习题 - 图7

  1. z = (460.4 - 423) / (101.9 / np.sqrt(36))
  3. # 上侧检验
  4. print(1 - norm.cdf(z))   # 0.0138

得出的概率值为0.0138，明显小于显著性水平0.05，因此我们甘愿冒着第一类错误的风险拒绝原假设，得出可乐可口饮料在亚特兰大的年平均销售量更高的结论。