
该数据集是通过研究消费者23个变量特征来判断他们是否使用信用卡作为默认支付方式
该项目可以迁移到商业场景中的其它项目中:
- 客户是否流失
- 客户是否购买
- 客户是否点击
- …
数据的23个特征如下,目标值是0/1的二分类
- X1: Amount of the given credit (NT dollar): it includes both the individual consumer credit and his/her family (supplementary) credit.
- X2: Gender (1 = male; 2 = female).
- X3: Education (1 = graduate school; 2 = university; 3 = high school; 4 = others).
- X4: Marital status (1 = married; 2 = single; 3 = others).
- X5: Age (year).
- X6 - X11: History of past payment. We tracked the past monthly payment records (from April to September, 2005) as follows: X6 = the repayment status in September, 2005; X7 = the repayment status in August, 2005; . . .;X11 = the repayment status in April, 2005. The measurement scale for the repayment status is: -1 = pay duly; 1 = payment delay for one month; 2 = payment delay for two months; . . .; 8 = payment delay for eight months; 9 = payment delay for nine months and above.
- X12-X17: Amount of bill statement (NT dollar). X12 = amount of bill statement in September, 2005; X13 = amount of bill statement in August, 2005; . . .; X17 = amount of bill statement in April, 2005.
- X18-X23: Amount of previous payment (NT dollar). X18 = amount paid in September, 2005; X19 = amount paid in August, 2005; . . .;X23 = amount paid in April, 2005.
数据引入与探索
加载模块
import numpy as npimport pandas as pdimport seaborn as snsimport matplotlib.pyplot as pltdf = pd.read_excel('default of credit card clients.xls')df.head()
执行
| ID | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | … | X15 | X16 | X17 | X18 | X19 | X20 | X21 | X22 | X23 | Y | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 20000 | 2 | 2 | 1 | 24 | 2 | 2 | -1 | -1 | … | 0 | 0 | 0 | 0 | 689 | 0 | 0 | 0 | 0 | 1 |
| 1 | 2 | 120000 | 2 | 2 | 2 | 26 | -1 | 2 | 0 | 0 | … | 3272 | 3455 | 3261 | 0 | 1000 | 1000 | 1000 | 0 | 2000 | 1 |
| 2 | 3 | 90000 | 2 | 2 | 2 | 34 | 0 | 0 | 0 | 0 | … | 14331 | 14948 | 15549 | 1518 | 1500 | 1000 | 1000 | 1000 | 5000 | 0 |
| 3 | 4 | 50000 | 2 | 2 | 1 | 37 | 0 | 0 | 0 | 0 | … | 28314 | 28959 | 29547 | 2000 | 2019 | 1200 | 1100 | 1069 | 1000 | 0 |
| 4 | 5 | 50000 | 1 | 2 | 1 | 57 | -1 | 0 | -1 | 0 | … | 20940 | 19146 | 19131 | 2000 | 36681 | 10000 | 9000 | 689 | 679 | 0 |
5 rows × 25 columns
常见探索
查看数据类型
df.dtypes
执行
ID int64X1 int64X2 int64X3 int64X4 int64X5 int64X6 int64X7 int64X8 int64X9 int64X10 int64X11 int64X12 int64X13 int64X14 int64X15 int64X16 int64X17 int64X18 int64X19 int64X20 int64X21 int64X22 int64X23 int64Y int64dtype: object
判断是否存在缺失值
df.isna().sum()
执行
ID 0X1 0X2 0X3 0X4 0X5 0X6 0X7 0X8 0X9 0X10 0X11 0X12 0X13 0X14 0X15 0X16 0X17 0X18 0X19 0X20 0X21 0X22 0X23 0Y 0dtype: int64
通过describe查看额度这个特征的分布
df['X1'].describe()
执行
count 30000.000000mean 167484.322667std 129747.661567min 10000.00000025% 50000.00000050% 140000.00000075% 240000.000000max 1000000.000000Name: X1, dtype: float64
查看数据框的shape
df.shape
执行
(30000, 25)
观察其中某一个样本
df.iloc[2]
执行
ID 3X1 90000X2 2X3 2X4 2X5 34X6 0X7 0X8 0X9 0X10 0X11 0X12 29239X13 14027X14 13559X15 14331X16 14948X17 15549X18 1518X19 1500X20 1000X21 1000X22 1000X23 5000Y 0Name: 2, dtype: int64
单特征探索
离散特征X2的分布
1 = male; 2 = female
df['X2'].value_counts()
执行
2 181121 11888Name: X2, dtype: int64
离散特征X3的分布
1 = graduate school; 2 = university; 3 = high school; 4 = others
df['X3'].value_counts().plot(kind='bar')
执行
<matplotlib.axes._subplots.AxesSubplot at 0x1240d0df0>
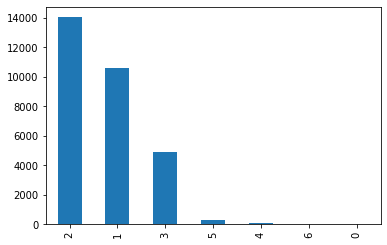
离散特征X4的分布
1 = married; 2 = single; 3 = others
df['X4'].value_counts()
执行
2 159641 136593 3230 54Name: X4, dtype: int64
目标值Y的分布
可以看到在当前的数据集中,目标值的分布是不均匀的
df['Y'].value_counts()
执行
0 233641 6636Name: Y, dtype: int64
分组探索
X2特征,按照性别进行分组,比较不同月份的账单
# 1 = male; 2 = femaledf.groupby(['X2']).agg({'X12': 'mean', 'X13': 'mean', 'X14': 'mean', 'X15': 'mean', 'X16': 'mean', 'X17': 'mean'}).plot(kind='bar')
执行
<matplotlib.axes._subplots.AxesSubplot at 0x1203be4f0>
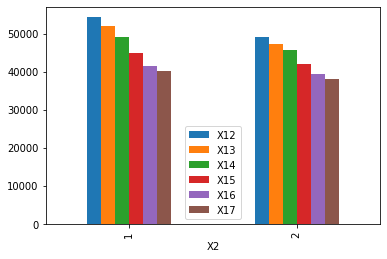
X2特征,按照性别进行分组,比较同一月份男性和女性的账单差异
# 1 = male; 2 = femaledf.groupby(['X2']).agg({'X12': 'mean', 'X13': 'mean', 'X14': 'mean', 'X15': 'mean', 'X16': 'mean', 'X17': 'mean'}).T.plot(kind='bar')
执行
<matplotlib.axes._subplots.AxesSubplot at 0x11feac850>
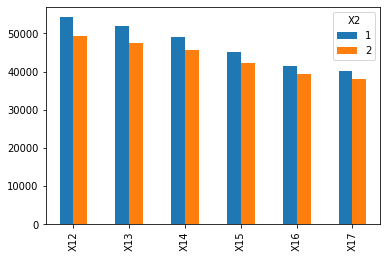
X2特征,按照性别进行分组,比较同一月份男性和女性的Amount of previous payment差异
# 1 = male; 2 = femaledf.groupby(['X2']).agg({'X18': 'mean', 'X19': 'mean', 'X20': 'mean', 'X21': 'mean', 'X22': 'mean', 'X23': 'mean'}).T.plot(kind='bar')
执行
<matplotlib.axes._subplots.AxesSubplot at 0x11feac520>
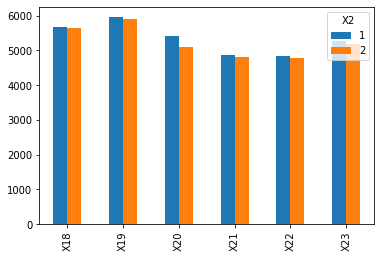
特征处理
我们的数据集中有3个离散特征,而scikit-learn中是没法直接将离散特征作为输入的;
因此需要对离散特征做one-hot-encoder操作,类似于我们在学习线性回归章节的哑变量(只能取值0或1)处理。
方法一:OneHotEncoder
我们可以使用sklearn中OneHotEncoder函数
生成哑变量对应的列
from sklearn.preprocessing import OneHotEncoderenc = OneHotEncoder()enc.fit(df.iloc[:, [2,3,4]])res = enc.transform(df.iloc[:, [2,3,4]]).toarray()
我们想看一下生成的结果是什么样子的?如下所示:
enc_data = pd.DataFrame(res)enc_data.head()
执行
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 |
| 1 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 2 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 3 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 |
| 4 | 1.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 |
对于上面这个表格,不禁想吐槽一句,这是什么鬼?我们来分析一下:
X2这个特征有1,2两种取值结果;X3这个特征有0,1,2,3,4,5,6共七种取值结果;X4这个特征有0,1,2,3共四种取值结果;因此2+7+4=13;就分别对应上面表格中的13列数据;
将哑变量与原有数据集横向拼接
train_data = pd.concat([df, enc_data], axis=1)train_data.head()
执行
| ID | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | … | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 20000 | 2 | 2 | 1 | 24 | 2 | 2 | -1 | -1 | … | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 |
| 1 | 2 | 120000 | 2 | 2 | 2 | 26 | -1 | 2 | 0 | 0 | … | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 2 | 3 | 90000 | 2 | 2 | 2 | 34 | 0 | 0 | 0 | 0 | … | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 |
| 3 | 4 | 50000 | 2 | 2 | 1 | 37 | 0 | 0 | 0 | 0 | … | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 |
| 4 | 5 | 50000 | 1 | 2 | 1 | 57 | -1 | 0 | -1 | 0 | … | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 |
5 rows × 38 columns
去除不需要的离散特征列
# 这三列特征我们是不会给模型学习的,应该丢弃掉train_data.drop(columns=['X2', 'X3', 'X4']).shape
执行
(30000, 35)
方法二:get_dummies
# 两个优点:1,自动去除掉原有的列 2,新增的列名定义的很清晰train_data = pd.get_dummies(df, columns=['X2', 'X3', 'X4'])train_data.head()
执行
| ID | X1 | X5 | X6 | X7 | X8 | X9 | X10 | X11 | X12 | … | X3_1 | X3_2 | X3_3 | X3_4 | X3_5 | X3_6 | X4_0 | X4_1 | X4_2 | X4_3 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 20000 | 24 | 2 | 2 | -1 | -1 | -2 | -2 | 3913 | … | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 2 | 120000 | 26 | -1 | 2 | 0 | 0 | 0 | 2 | 2682 | … | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 2 | 3 | 90000 | 34 | 0 | 0 | 0 | 0 | 0 | 0 | 29239 | … | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 3 | 4 | 50000 | 37 | 0 | 0 | 0 | 0 | 0 | 0 | 46990 | … | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 4 | 5 | 50000 | 57 | -1 | 0 | -1 | 0 | 0 | 0 | 8617 | … | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
5 rows × 35 columns
训练模型
随机森林模型
fit
from sklearn.ensemble import RandomForestClassifier# 构建10棵决策树rfModel = RandomForestClassifier(n_estimators=10)# 去除掉输入数据集中不需要的列X = train_data.drop(columns=['ID', 'Y'])Y = train_data['Y']rfModel.fit(X, Y)
执行
RandomForestClassifier(bootstrap=True, ccp_alpha=0.0, class_weight=None,criterion='gini', max_depth=None, max_features='auto',max_leaf_nodes=None, max_samples=None,min_impurity_decrease=0.0, min_impurity_split=None,min_samples_leaf=1, min_samples_split=2,min_weight_fraction_leaf=0.0, n_estimators=10,n_jobs=None, oob_score=False, random_state=None,verbose=0, warm_start=False)
我们可以从它的参数中看出随机森林默认最优特征的选取是基于基尼系数的;连续特征作离散化处理;计算量很大;
评估
使用score方法查看模型准确率,又当裁判又当运动员,这种方式有作弊的嫌疑,不太可取;
rfModel.score(X, Y)
执行
0.9797333333333333
还记得我们之前学习过的OOB SCORE吗?通过未被模型学习过的样本进行预测,这样才有可靠性;
# 设置oob_score参数为TruerfModel = RandomForestClassifier(n_estimators=10, oob_score=True)rfModel.fit(X, Y)# 查看模型准确率rfModel.oob_score_
执行
0.7822
这个78%的正确率才是比较合理的
提高模型复杂度
# 构建100棵决策树rfModel = RandomForestClassifier(n_estimators=100, oob_score=True)rfModel.fit(X, Y)rfModel.oob_score_
执行
0.8151666666666667
此时,正确率已经达到了81.5%;相比于我们之前10棵决策树时,提高了3个百分点;
# 设置最大深度为10rfModel = RandomForestClassifier(n_estimators=100, oob_score=True, max_depth=10)rfModel.fit(X, Y)rfModel.oob_score_
执行
0.8195333333333333
此时,正确率达到了81.9%;相比于我们上面的100棵决策树,提高了40个基点;(一个基点是0.01%)
要知道模型的效果,是越往上越难提升;因为数据本身的限制,以及模型的学习方式,它的效果是存在上限的;
决策树模型
from sklearn.tree import DecisionTreeClassifierdtc = DecisionTreeClassifier(max_depth=10)dtc.fit(X, Y)dtc.score(X, Y)
执行
0.8461333333333333
即便是这种不太公平的对决(既当裁判又当运动员),随机森林的效果(约98%)也远胜于单一决策树;
公平的对比决策树与随机森林
accuracy方法
划分数据集为训练集和测试集
from sklearn.model_selection import StratifiedShuffleSplitsf = StratifiedShuffleSplit(n_splits=1, test_size=0.2)for train_index, test_index in sf.split(X, Y):train_X, test_X = X.iloc[train_index], X.iloc[test_index]train_Y, test_Y = Y.iloc[train_index], Y.iloc[test_index]
这里之所以使用StratifiedShuffleSplit方法,是为了尽可能确保我们的训练集和测试集中样本的分布是成比例的;(保证类别0和类别1的比例与原始数据集中是一致的)当然你也可以进行随机抽样手动划分;
print(train_X.shape) # (24000, 33)print(test_X.shape) # (6000, 33)print(train_Y.shape) # (24000,)train_Y
执行
3847 010087 06901 027103 08097 0..9342 013619 120637 019574 05944 0Name: Y, Length: 24000, dtype: int64
决策树学习
dtc = DecisionTreeClassifier(max_depth=10)dtc.fit(train_X, train_Y)# 使用测试数据集评估dtc.score(test_X, test_Y)
执行
0.8081666666666667
随机森林学习
rfModel = RandomForestClassifier(n_estimators=100, max_depth=10)rfModel.fit(train_X, train_Y)# 与上述oob_score对比你会发现两者比较接近,验证了oob_score的有效性rfModel.score(test_X, test_Y)
执行
0.8183333333333334
我们可以看到相对来说,随机森林的效果是要好于决策树的;然而这里面却有一个严重的缺陷;
大缺陷
我们可以看到,在我们的测试数据集中,类别1有1327个,类别0有4673个;
np.unique(test_Y, return_counts=True)
执行
(array([0, 1]), array([4673, 1327]))
假设我们不管三七二一,把测试集所有的样本都预测为类别0,这种情况下模型的正确率有多少呢?
4673 / (4673 + 1327)
执行
0.7788333333333334
可以看到,即便瞎猜的,模型的正确率也有77.8%;
因此,使用正确率这个指标来对比随机森林和决策树模型的效果是不恰当的;
使用roc曲线更公平的对比
决策树
# roc_auc_score可以很好的消除这种样本不均衡带来的评估影响
from sklearn.metrics import roc_auc_score
# 输出的结果为类别值的概率值
dtc_predict = dtc.predict_proba(test_X)
dtc_predict
执行
array([[0.83280255, 0.16719745],
[0.29149798, 0.70850202],
[0.98076923, 0.01923077],
...,
[0.83280255, 0.16719745],
[0.91752577, 0.08247423],
[0.15503876, 0.84496124]])
注意:这是一个二维的数组,第0列表示预测值为类别0的概率,第1列表示预测值为类别1的概率
# 获取类别值为1的概率
dtc_predict = dtc_predict[:, 1]
# 真实的label和预测的label作比较
roc_auc_score(test_Y, dtc_predict)
执行
0.7261580297984009
可以看到结果为72.6%;
随机森林
# 获取类别值为1的概率
rfModel_predict = rfModel.predict_proba(test_X)[:, 1]
# 真实的label和预测的label作比较
roc_auc_score(test_Y, rfModel_predict)
执行
0.7721940290636891
结果为77.2%;相对于决策树来讲,提升了5个百分点,已经算是提升很大的了;
特征重要性
哪些特征重要
rfModel = RandomForestClassifier(n_estimators=100, max_depth=10)
rfModel.fit(X, Y)
执行
RandomForestClassifier(bootstrap=True, ccp_alpha=0.0, class_weight=None,
criterion='gini', max_depth=10, max_features='auto',
max_leaf_nodes=None, max_samples=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=100,
n_jobs=None, oob_score=False, random_state=None,
verbose=0, warm_start=False)
通过featureimportances属性,我们可以看到哪些特征相对比较重要
rfModel.feature_importances_
执行
array([3.59942809e-02, 2.30633923e-02, 2.48168743e-01, 1.14646345e-01,
6.04621758e-02, 5.68672273e-02, 5.88615783e-02, 3.22794928e-02,
3.24865008e-02, 2.99892679e-02, 2.71754611e-02, 2.60024289e-02,
2.52445532e-02, 2.59896530e-02, 3.99988873e-02, 3.34622517e-02,
2.92641917e-02, 2.47773719e-02, 2.37720527e-02, 2.54647251e-02,
3.37819462e-03, 3.21148967e-03, 6.65792514e-07, 4.16449451e-03,
3.10293159e-03, 3.02263322e-03, 1.57962602e-04, 9.79727323e-04,
3.66076691e-04, 2.69770331e-04, 3.27758513e-03, 3.17172365e-03,
9.26164452e-04])
可视化的方式进行展现
plt.rcParams['figure.figsize'] = (10.0, 8.0)
feature_importances = pd.Series(rfModel.feature_importances_, index=X.columns)
feature_importances.sort_values().plot(kind='bar')
执行
<matplotlib.axes._subplots.AxesSubplot at 0x12a1e9730>
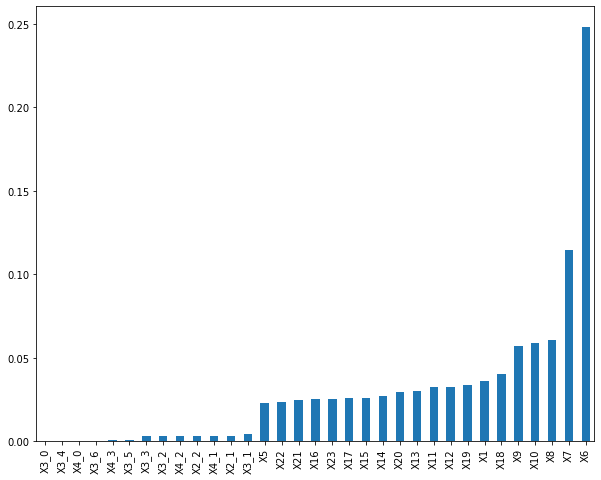
有了特征的重要程度,我们可以做两件事情
- 可以对业务进行解释,哪几个特征相对来说比较重要
- 可以对重要性大的特征作进一步的挖掘和探索
更多特征工程
def cat_values(df, categorical_columns, target_columns):
j = 0
for c in categorical_columns:
# 分组后做了标准化处理 每次循环新增 len(target_columns) 列
grouped = df.groupby(c)
result1 = grouped[target_columns].transform(lambda s: (s - s.mean()) / s.std())
result1.columns = [col + '_' + str(j) for col in target_columns]
j += 1
df = pd.concat([df, result1], axis=1)
# 左连接 每次循环新增 2 * len(target_columns) 列
result = grouped[target_columns].agg(['mean', 'std'])
result.columns = [t + aggfunc for t in target_columns for aggfunc in ['_mean', '_std']]
df = pd.merge(df,result,left_on=c,right_index = True)
return df
data = cat_values(df,['X2','X3','X4'],['X6','X7','X8','X9','X10'])
print(data.shape) # (30000, 70)
train_data = pd.get_dummies(data=data, columns=['X2', 'X3', 'X4'])
print(train_data.shape) # (30000, 80)
对下面随机森林方法中涉及到的参数作一个简单说明:n_jobs设置为-1,有多少线程跑多少线程;max_features 特征的采样最多70%
rfModel = RandomForestClassifier(n_estimators=200, max_depth=10, n_jobs=-1, oob_score=True, max_features=0.7)
X = train_data.drop(columns = ['ID', 'Y'])
Y = train_data['Y']
rfModel.fit(X, Y)
执行
RandomForestClassifier(bootstrap=True, ccp_alpha=0.0, class_weight=None,
criterion='gini', max_depth=10, max_features=0.7,
max_leaf_nodes=None, max_samples=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=200,
n_jobs=-1, oob_score=True, random_state=None, verbose=0,
warm_start=False)
查看一下oob_score
rfModel.oob_score_
执行
0.8210666666666666

