第一题 餐厅销售额

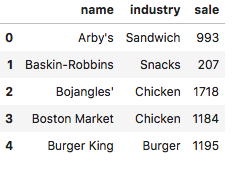
名为 FoodIndustry 的文件包含的数据有连锁店的名字、每个店的平均销售额(单位：1000美元)和47家连锁餐厅对应的食品细分行业。

  1. 对于 47 家连锁餐厅，每个店的平均销售额是多少?
  2. 第一四分位数和第三四分位数是多少?你怎么解释四分位数?
  3. 绘制销售水平的箱形图，并讨论销售额方面是否有异常值，是否偏离结果？
  4. 对每一个细分行业，编制反映每个店销售额的频数分布，并对所得结果加以评论。

解答：

  1. import numpy as np
  2. import pandas as pd
  4. df = pd.read_csv('FoodIndustry.csv', names=['name', 'industry', 'sale'], header=0)
  5. df.head()

我们先有一个数据的轮廓：
image.png

第一问

  1. df['sale'].mean()                # 1275.1914893617022

因此我们得出，总共47家店，平均每个门店的销售额约为127.5万美元。

第二问

  1. df['sale'].describe()

执行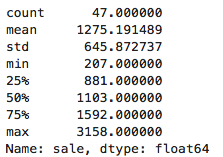
image.png
可以看到，第一四分位数为88.1万美元，第三四分位数为159.2万美元
大约有25%的门店销售额是小于88.1万美元的，大约有25%的门店销售额是大于159.2万美元的

第三问

  1. df['sale'].plot(kind='box')

执行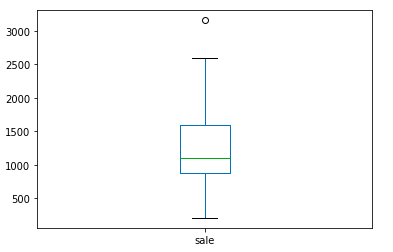
image.png
从上面这个图，我们一眼就可以看出来是存在异常值的，根据前面的describe输出，我们知道该异常值为315.8
我们顺带看一下是哪家门店如此优秀？

  1. df[df['sale'] == 3158]

执行
image.png
可以看到是Chick-fil-A这家门店，所属的细分行业是鸡肉，有可能是门店的促销活动起了大作用，但谁知道呢

第四问

  1. # 获取鸡肉该细分行业的销售额数据
  2. tmp_df = df.loc[df['industry'] == 'Chicken']['sale']
  4. # 将连续型数值变量转化为分类变量
  5. df['group'] = pd.cut(tmp_df, bins=5, right=True, include_lowest=True)
  6. pd.DataFrame(df['group'].value_counts())

执行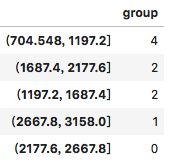
image.png
说明在鸡肉这个细分行业里，有一半的门店销售额是在70.4万美元到119.7万美元之间。大部分门店的销售额是平均偏下的，只有一家门店的销售额比较突出。

第二题 烟雾探测器

过去40年，美国拥有烟雾探测器的家庭比例持续上升，并稳定在大约96% (NationalFireProtec-tionAssociationwebsite，2015年1月)。由于烟雾探测器使用的增加，家庭火灾死亡率有何变化？文件 SmokeDetector 包含了17年间拥有烟雾探测器的家庭比例和每 100 万人口家庭火灾死亡率的估计数据。

  1. 你期待烟雾探测器的使用和家庭火灾死亡率之间是正相关还是负相关？为什么？
  2. 计算相关系数。烟雾探测器的使用和家庭火灾死亡率之间是正相关还是负相关？请加以评论。
  3. 绘制每 100 万人口死亡率和拥有烟雾探测器家庭比例之间关系的散点图。

解答：

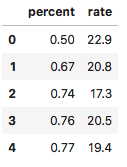
  1. df = pd.read_csv('SmokeDetectors.csv', names=['percent', 'rate', 1, 2], header=0)
  2. df = df[['percent', 'rate']]
  3. df = df.dropna()
  4. df.head()

先有一个数据的轮廓
image.png

第一问

猜测为负相关，烟雾报警器使用得多了，家庭中大火灾发生的可能性就会降低，能够在火灾发生的初始阶段就把小火苗扑灭，死亡率也会随之下降。

第二问

根据皮尔逊相关系数公式：描述统计学习题 - 图7
根据协方差计算公式：描述统计学习题 - 图8

我们依次进行计算：
描述统计学习题 - 图9

  1. # 计算平均数
  2. avg_percent = df['percent'].mean()
  3. avg_rate = df['rate'].mean()
  5. # 计算样本协方差
  6. sxy = np.sum((df['percent'] - avg_percent) * (df['rate'] - avg_rate)) / (len(df) - 1)
  8. # 计算样本标准差
  9. sx = df['percent'].std()
  10. sy = df['rate'].std()
  12. # 计算相关系数
  13. r = sxy / (sx * sy)
  14. r                                # -0.9059552875657785

我们可以从计算结果看到，数值是很接近-1了。
即烟雾探测器的使用和家庭火灾死亡率之间存在着强的负线性关系。
更具体的说，随着烟雾探测器的使用增加，家庭火灾死亡率逐渐降低，但这并不意味着它们之间存在因果关系。

这里补充一个小插曲：
起初我在计算标准差时，使用的是np.std，后来发现该计算结果和自己手动按照标准差公式计算出的数据有出入，上网查了一下，原来np.std计算的总体标准差，而pd.std则计算的是样本标准差。

第三问

  1. import matplotlib.pyplot as plt
  2. plt.scatter(x='percent', y='rate', data=df)

执行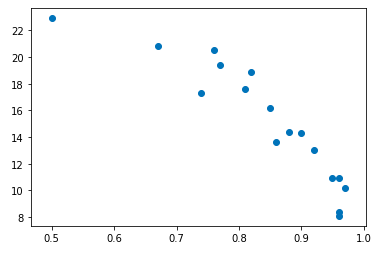
image.png
从图中我们可以看到，左上角的这个数据点，明显是属于一个异常值。

第三题 橄榄球教练

《今日美国》报道美国大学生体育协会 (NCAA)学院和大学向新招聘的橄榄球教练支付比前任橄榄球教练更高的工资(《今日美国》，2013年2月12日）。数据文件 Coaches 给出了 23 所学院和大学前任和现任橄榄球主教练的基础薪资。

  1. 分别确定前任和现任橄榄球主教练的中位数年薪。
  2. 分别计算前任和现任橄榄球主教练的极差。
  3. 分别计算前任和现任橄榄球主教练的标准差。
  4. 根据(1)~(3)的结果，就一所学校对现任橄榄球主教练与前任橄榄球主教练相比支付的基础年薪之间的不同发表评价。

解答：

  1. df = pd.read_csv('Coaches.csv', names=['School', 'Previous Salary', 'New Salary', 1], header=0)
  2. df = df.iloc[:,:3]
  3. df.head()

先看一下数据的轮廓：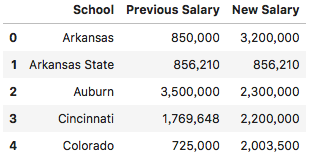
image.png

第一问

我们注意薪水这两列的数据存在千位分隔符，同时还有空格的情况，因此我们要先对数据进行清洗一下。

  1. # 处理千位分隔符
  2. df['Previous Salary'] = df['Previous Salary'].apply(lambda s: int((s.strip().replace(',', ''))))
  3. df['New Salary'] = df['New Salary'].apply(lambda s: int((s.strip().replace(',', ''))))
  5. previous = df['Previous Salary'].median()
  6. new = df['New Salary'].median()
  8. print(previous)                        # 850000.0
  9. print(new)                            # 1150000.0

即前任橄榄球主教练的薪资中位数在85万美元，而现任橄榄球主教练的薪资中位数在115万美元。

第二问

  1. print(df['Previous Salary'].max() - df['Previous Salary'].min())    # 3232200
  2. print(df['New Salary'].max() - df['New Salary'].min())              # 2920000

即前任橄榄球主教练的极差在323万美元，现任橄榄球主教练的极差在292万美元。（果然人比人，气死人）

第三问

  1. print(df['Previous Salary'].std())            # 1004739.5463241073
  2. print(df['New Salary'].std())               # 901872.5331704873

可以看到，前任橄榄球主教练的年薪变异程度相对现任要大一些。

第四问

就Arkansas学校而言，现任橄榄球主教练的年薪是前任的将近三倍还要多，而且远远大于现任橄榄球主教练的中位数薪资，应该能说明两点：Arkansas现任橄榄球主教练的技术水平很高；该学校希望大力发展提高橄榄球运动。