描述统计


第一步要做的就是了解熟悉数据：主要是历史逾期还款期数这一列数据。**

  1. import pandas as pd
  2. import numpy as np
  4. df = pd.read_csv('LC.csv', )
  5. df.head()

执行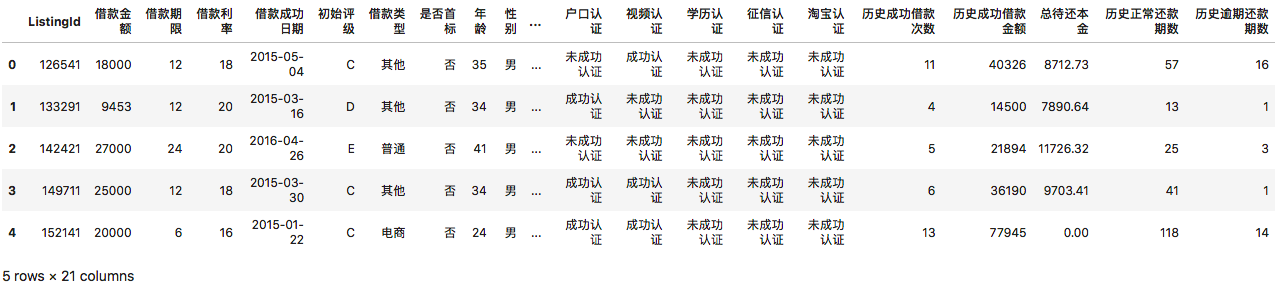
image.png
看一下数据都有哪些列？

  1. df.columns

执行
image.png
我们看到数据中有一列是ListingId，看起来很像是索引，检查一下该列数据是不是唯一？

  1. df['ListingId'].nunique() == len(df)             # False

因此我们不能把该列设置为索引列。该列应该是借款人的Id。同一个借款人可以同时有多笔借款记录。
看一下数据的规模：

  1. df.shape                                         # (4517, 21)

选取第一行数据看一下：

  1. df.loc[0]

执行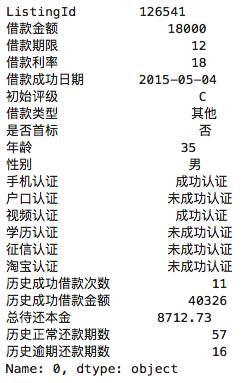
image.png
初始评级有哪些等级呢？

  1. df['初始评级'].unique()        # array(['C', 'D', 'E', 'A', 'B', 'F'], dtype=object)

最后，最重要的通过describe方法查看一下我们感兴趣的列

  1. df[['借款金额','借款期限','借款利率','年龄','历史成功借款次数',
  2.     '历史成功借款金额','总待还本金','历史正常还款期数','历史逾期还款期数']].describe()

执行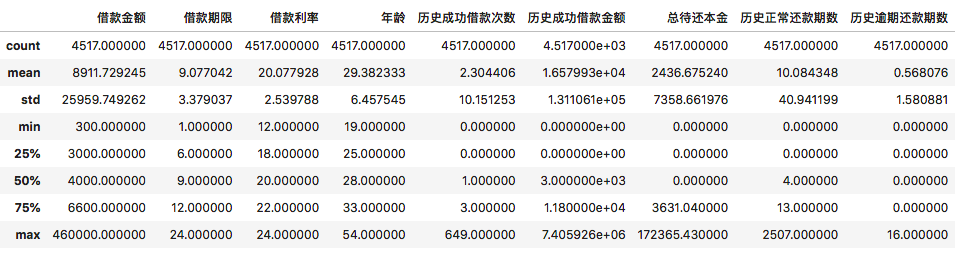
image.png
从”历史逾期还款期数“这一列的输出来看，大部分人都有良好的还款记录，平均的逾期次数为0.58。
那逾期还款的记录占比是多少呢？

  1. (df['历史逾期还款期数'] != 0).sum() / len(df)                # 0.22382112021253045

可视化

我们想知道历史逾期还款期数这一列的数据分布是怎样的？是否是正态分布吗？最直观的方式就是通过柱状图。
画图之前，我们需要先检查一下数据：

  1. df['历史逾期还款期数'].unique()

执行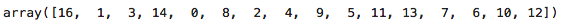
image.png

  1. # 离散型变量 我们用柱状图
  2. df['历史逾期还款期数'].value_counts().sort_index()

执行
image.png
真正开始画图，我们绘制针对具体逾期次数的记录所占总记录的百分比图：

  1. import matplotlib.pyplot as plt
  3. tmp = df['历史逾期还款期数'].value_counts().sort_index()
  4. plt.bar(tmp.index, tmp.values/len(df))

执行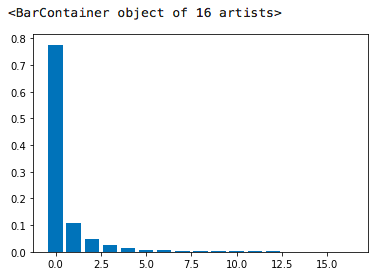
image.png
我们可以清晰的看到，数据严重右偏。这和我们前面describe方法输出的结果是一致的，应该至少有75%的记录是0次违约的，即大部分人都是有良好还款记录的。

相关性分析

  1. plt.scatter(x=df['总待还本金'], y=df['历史逾期还款期数'])

执行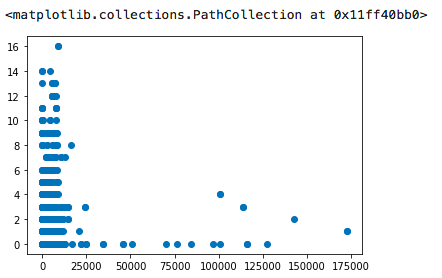
image.png
这两个变量间并没有明显的线性关系，至少从这4000多条记录看，是这个样子。

  1. df[['历史逾期还款期数', '征信认证']].groupby(['征信认证'])
  2.     .agg(['mean', 'std', 'max', 'min', 'count'])

执行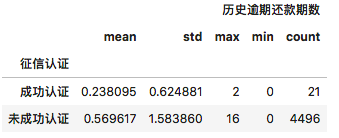
image.png
可以明显看到，征信认证还是非常管用的，逾期还款期数平均值缩小了一半还要多。

  1. df[['历史逾期还款期数', '性别']].groupby(['性别'])
  2.     .agg(['mean', 'std', 'max', 'min', 'count'])

执行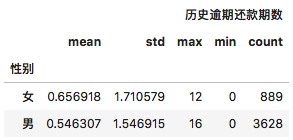
image.png
从这个结果看，女性要比男性的平均逾期还款次数大，且不稳定性也大。似乎是男性在这方面表现的比女性要好。这着实有点出乎意料。

  1. plt.scatter(x=df['初始评级'], y=df['历史逾期还款期数'])

执行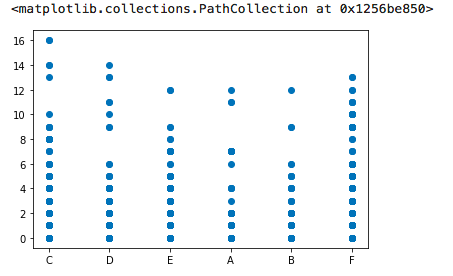
image.png
本以为初始评级会对逾期还款次数会有明显影响，从这里看，并不是这个样子。

假设检验

我们对总待还本金，设计一个实验，作一个假设检验：

  1. total_avg = df['总待还本金'].mean()
  2. print(total_avg)                            # 2436.675240203675
  4. total_std = df['总待还本金'].std()
  5. print(total_std)                            # 7358.661975694644
  7. df['总待还本金'].describe()

执行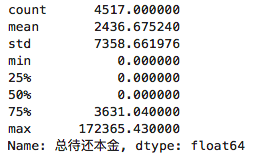
image.png

  1. plt.hist(df['总待还本金'], bins=20)

执行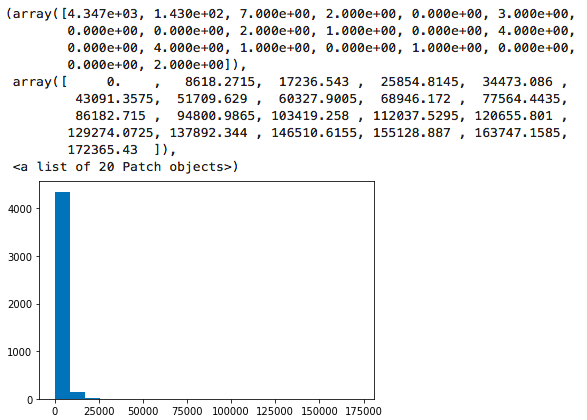
image.png
数据严重右偏，我们抽样时，选取样本容量可得用心了。

  1. # 模拟随机抽样
  2. data = df['总待还本金'].sample(frac=0.1)
  4. print(data.mean())      # 2684.8759734513274
  6. print(data.std())       # 9546.555029497065

假设我们认为总待还金额在2400元以内则是风险可控的，总体标准差未知，研究样本数据，在0.05的显著性水平下，是否可以得出”总体数据的总待还金额是风险可控的“结论呢？

建立假设：**
逾期还款---金融 - 图14 逾期还款---金融 - 图15

显著性水平：0.05

计算样本统计量：

  1. from scipy.stats import t
  3. n = len(df) * 0.1
  4. s = data.std() / np.sqrt(n)
  5. z = (data.mean() - 2400) / s
  7. # 属于是上侧检验
  8. p = 1 - t.cdf(z, n - 1)
  9. p                                    # 0.26313224614031694

可以看到p值大于显著性水平，如果不能拒绝原假设，那么犯第二类错误的概率是多少呢？

  1. z = t.ppf(0.975, n - 1) 
  2. tmp = z * s + 2400
  3. print(tmp)                    # 3282.7496355352687

即当样本均值大于等于3283时，拒绝原假设，进一步得出：当样本均值小于3283时，接受原假设；

  1. # 1，假定原假设为假，即选取一个大于2400的总体均值，这里选择3000
  2. # 2，求假定均值为3000时，小于3283的概率
  4. z = (tmp - 3000) / s
  6. p = t.cdf(z, n - 1)
  7. p                        # 0.7353223767289456

这里我们计算出，犯第二类错误的概率为0.735，还是很高的。