数据挖掘导论

与数据分析的区别

数据分析前置知识：（业务岗）

• Python
• 概率统计

数据挖掘前置知识：（技术岗）

• 掌握数据分析是大前提
• 微积分(重中之重)
• 线性代数

什么是机器学习

背景

对于新手来讲，可将机器学习等同于数据挖掘。

机器学习是人工智能的一个分支。人工智能的研究是从以“推理”为重点到以“知识”为重点，再到以“学习”为重点，一条自然、清晰的脉络。显然，机器学习是实现人工智能的一个途径，即以机器学习为手段解决人工智能中的问题。机器学习在近30多年已发展为一门多领域交叉学科，涉及概率论、统计学、逼近论、凸分析、计算复杂性理论等多门学科。机器学习理论主要是设计和分析一些让计算机可以自动“学习”的算法。机器学习算法是一类从数据中自动分析获得规律，并利用规律对未知数据进行预测的算法。因为学习算法中涉及了大量的统计学理论，机器学习与推断统计学联系尤为密切，也被称为统计学习理论。（推荐书籍《统计学习方法》作者李航，人手一本）算法设计方面，机器学习理论关注可以实现的，行之有效的学习算法。很多推论问题属于无程序可循难度，所以部分的机器学习研究是开发容易处理的近似算法。

机器学习已广泛应用于数据挖掘、计算机视觉、自然语言处理、生物特征识别、搜索引擎、医学诊断、检测信用卡欺诈、证券市场分析、DNA序列测序、语音和手写识别、战略游戏和机器人等领域。

定义

机器学习有下面几种定义：

1. 机器学习是一门人工智能的科学，该领域的主要研究对象是人工智能，特别是如何在经验（其实就是数据）学习中改善具体算法的性能。
2. 机器学习是对能通过经验自动改进的计算机算法的研究。
3. 机器学习是用数据或以往的经验，以此优化计算机程序的性能标准。

机器学习的英文定义如下：（摘自维基百科）
A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.

机器学习的种类

监督学习

监督学习从给定的训练数据集中学习出一个函数，当新的数据到来时，可以根据这个函数预测结果。监督学习的训练集要求是包括输入和输出，也可以说是特征和目标。训练集中的目标是由人标注的。常见的监督学习算法包括回归分析（针对目标值是连续的）和统计分类（针对目标值是离散的）。

无监督学习

无监督学习与监督学习相比，训练集没有人为标注的结果。常见的无监督学习算法有聚类。

半监督学习

半监督学习介于监督学习和无监督学习之间。

增强学习

增强学习通过观察来学习做成如何的动作。每个动作都会对环境有所影响，学习对象根据观察到的周围环境的反馈来做出判断。

代价函数

线性回归中的案例

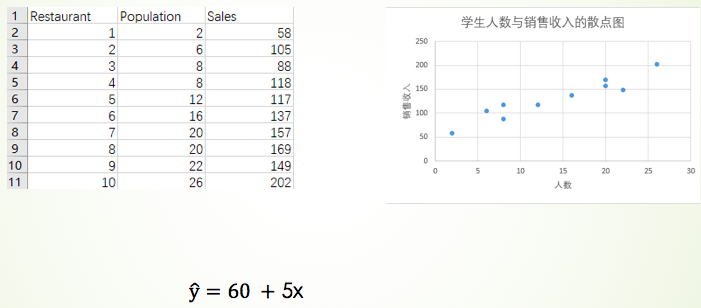
之前我们是通过最小二乘法计算出了估计的简单线性回归方程。下面换一种方式来求解。

模型的建立

约定下面几种符号的含义：

• m 表示样本的数量，这里 m=10
• n 表示每条样本特征的数量，这里 n = 1，即就一个特征Population
• 表示第 i 条样本，使用上标表示
• 表示某条样本的第 j 个特征，使用下标表示
• 表示截距
• 表示自变量 前的系数

我们简单线性回归的模型如下所示：

代价函数如下：（代价函数是用来衡量真实值与预测值之间误差的一种函数，一般用 表示）

相比于最小二乘法，只是前面多了 ，将上式中的预测值 替换为我们的模型表达式可得：

我们想办法让上面这个代价函数取值最小即可，在该式中，只有参数 是未知的，其它的都是已知。

注意：所有的监督学习都存在代价函数。

定义

性质

• 每种算法的代价函数不是唯一的（比如除了平方，还可以加绝对值等，有其它形式）
• 代价函数是参数θ的函数
• 总的代价函数J(θ)可以用来评价模型的好坏
• J(θ)是一个标量，一个实数，是可比较的

很自然的想到，令代价函数的值达到最小，即可求出最佳的参数θ，即求解 。求最小值，我们想到了什么？导数在这里就派上用场了，在印象中求解一元二次方程时，令导数取值为0，就对应着因变量的极值（最小值或最大值）。在这里最常用的方法是梯度下降法，这里的梯度就是 对 的偏导数。

常见面试题

写出简单线性回归的代价函数？就是1/2m * 最小二乘法公式，即

前置导数知识

• 加法的求导：可对每一项先求导再相加
• 减法的求导：可对每一项先求导再相减
• 乘法的求导： 求导可得：
• 偏导数：对谁求偏导，就只关注它，其它的则视为常数
• 更多求导知识可参考后面的微积分小节

梯度求解

回忆下我们前面得出的代价函数：

我们对 求偏导，使用偏导符号 可写成如下形式：（在这里 j 取值1或2）

令 j = 0 ，即对 求偏导可得：

令 j = 1 ，即对 求偏导可得：

注意：上面的求导过程中，涉及到了复合函数的求导，应用链式法则，先对外层求导，再对内层求导。

梯度下降算法

其中参数 为学习率，又称为步长，表示每次更新的有多快。步长大，运行时间快，但容易错过最优解；步长小，运行时间慢，不容易错过最优解；其中大括号包裹的称之为梯度，是对参数θ的偏导数。

因此，我们可以得到下面的迭代公式：

这里面哪些参数是未知的？其中 是我们要求解的参数，是未知的； 也是未知的，不过我们可以自定义，即手动地选择一个学习率。这里我们假设 已知，进行下面的步骤：

开始条件：随机给出θ0和θ1的两个值，通常情况下初始值都很小，比如为 0.01 和 0.001，一般初始值不为0。

如何迭代？每次传入一个样本，可以计算出对应的梯度，即偏导数结果（注意：上一步θ0和θ1此时可代入计算）。进一步通过迭代公式可以得到参数θ0和θ1的更新。

终止条件？不断重复，直到θ收敛，收敛即值不再发生变化或在一个很小区间内变化；或者已经消耗完所有的样本。

为什么以自我迭代的方式求解是可行的呢？看一下下面这个图：（梯度保证了我们是不断往下走的）

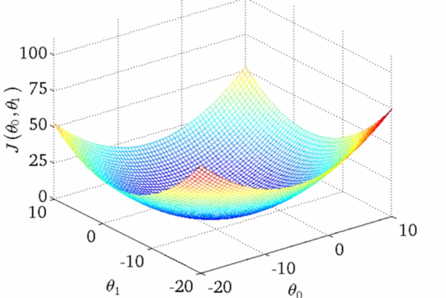
常见代价函数

回归分析中，均方误差是最常见的：

分类分析中，交叉熵是最常见的：



上式为逻辑斯蒂回归的代价函数。其中 要么取0要么取1， 表示为类别1的概率值。

模型泛化能力

泛化能力可理解为通用性，是对未知数据的预测能力。如果一个模型只在某份样本数据上表现良好，在其它样本数据上表现差，则该模型的可泛化能力差；另外一个概念是“过拟合”。如果模型对某份样本数据过度拟合了，那它的泛化能力肯定不好。

在统计上，我们追求的是模型的可解释性。比如前面的 中每个参数有什么含义等；我们使用判断系数 来评估模型的好坏。但这是不合理的，为什么？同一份数据既用来建模又用来评估，属于是又当裁判又当运动员的情况。

在机器学习中，我们追求的是模型对新鲜事物的可预测性。当新的样本到来时，我们模型预测的准确性怎么样；为了避免既当运动员又当裁判的情况出现，我们应该使用模型没有见过的数据去评估模型的准确性。通常采取的办法是对初始数据集进行分割。比如70%数据（Train Data）用来给模型训练，30%数据（Test Data）用来测试，即这30%模型没有见过的数据用来预测（Predict）评估模型的可泛化能力。

模型过拟合

我们先来看三个模型：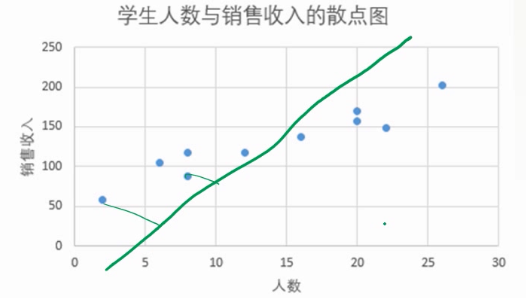

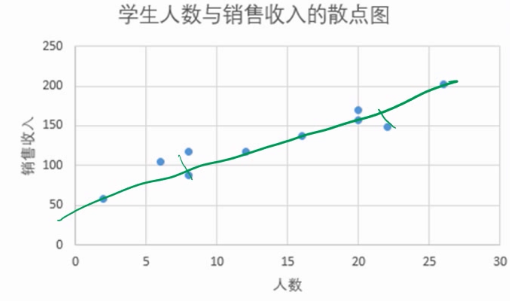
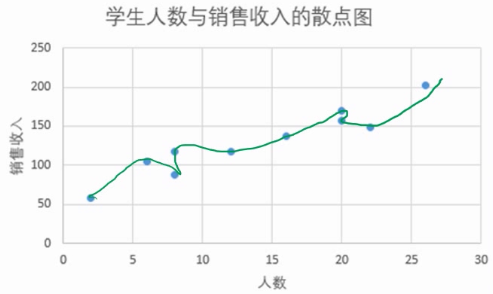
哪个模型效果最好？第二张图对应的模型效果最好。

第一张图对应的模型属于是 underfitting，模型根本没拟合好。解决办法：继续训练就好了，在实际中并不常见。

第三张图对应的模型属于是 overfitting，模型拟合过头了。什么原因造成的？可能因素有许多，比如样本数量太少，模型太过复杂等。在实际中较为常见。

如何解决过拟合的问题呢？

首要的就是不要在训练集上做模型的评估。另外可以通过在损失函数中添加正则项来尽可能避免。

即：

其中第二个加数为正则项（Regelization），λ 为惩罚项系数，它越大模型拟合程度越差，惩罚过头，模型就畏畏缩缩不敢动了。