模型学习

模型机制

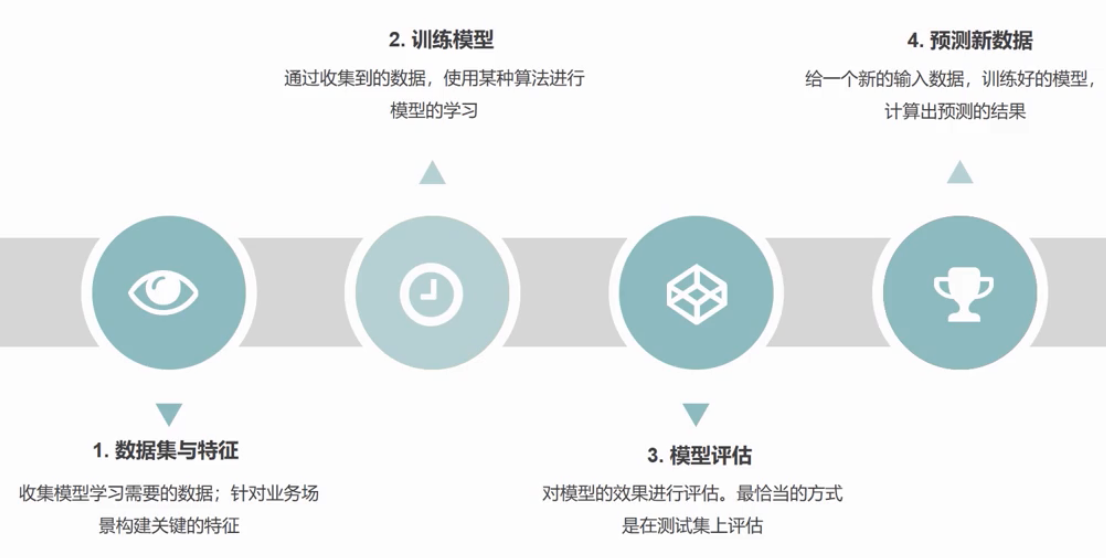
模型机制.png

无论是数据分析，数据挖掘，还是机器学习，模型的机制都是通用的，我们大部分时间都是在收集数据，构建特征。

决策树介绍

决策树.png

决策树模型

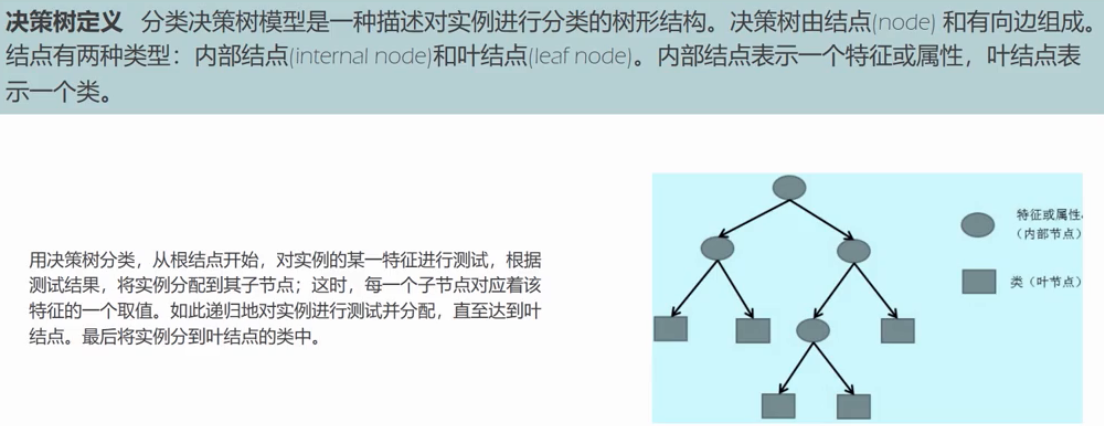
决策树模型.png

这里，我想说一下这里的实例是什么意思？就是一条条样本，比如我们线性回归中的抽样数据，每一行数据就代表一个样本。

决策树学习

决策树学习.png

为什么可能会产生多个决策树？因为我们选取的特征不同，顺序不同，都会得到不同的决策树，就看哪个好了

这里解释一下泛化能力：指的是该模型在新的数据集上也有很好的表现。

怎么来挑选好的决策树模型？上面两点结论都说了，一个是训练的好，一个是泛化的好。

怎么从条件概率模型来理解？输入了一些特征，然后我们要求的是在这些特征的前提下，Y为某一特定类别的概率。

决策树学习步骤.png

什么叫能够被基本正确分类？就是可以统一确定这些样本的类别值了。（比如之前 salary 小于50000美元的样本，就直接得出了 decline 的类别结果）

什么叫不能被基本正确分类？就是无法统一确定这些样本的类别值，还需要再选取特征进行划分。（比如之前 salary 大于50000美元的样本，就再次选取了 commute time 作为特征进行划分）

接下来，我们心里就要问问题了？要怎么选取最优特征，才能使得各个子集在当前条件有最好的分类呢（这就对应第二个大标题了）

决策树剪枝

决策树剪枝.png

先理解一下什么是过拟合？指的是在训练数据集上表现很好，但在新的数据集上却表现糟糕

之前，我们不断选取最优特征，进行特征空间的划分，是为了能训练好我们的决策树模型，但没有考虑泛化能力；这里的剪枝操作，就是使得模型的泛化能力更强

案例引入

案例引入.png

特征选择

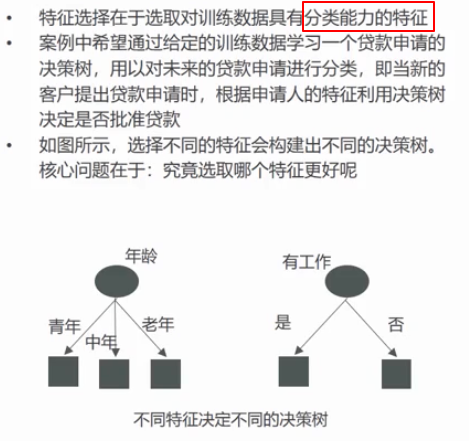
特征选择1.png

这就说明了针对每一个特征，肯定有个指标，可以用来衡量它的分类能力

熵的定义

熵的定义.png

简单回忆一下什么是随机变量？比如x的值，表示1万个学生的身高记录（连续型随机变量），1万个学生的年龄记录，一万个学生所使用手机的类别（离散型随机变量）

我们之前学习过使用方差来衡量一组数据的变异性（不确定性），这里的熵是更为科学的一种方式

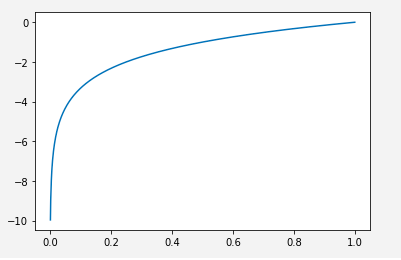
看一下log以2为底的函数是什么样子的（x的值无限逼近于0，但永远不可能为0；当x取值为1时，y值为0）

log以2为底.png

我们尝试输出一下，假设只有2个类别，即2元分类问题熵定义的函数图形（参照我们上面得出的公式）

  1. import numpy as np
  2. import matplotlib.pyplot as plt
  4. X = np.linspace(0, 1, 1000)
  5. Y = -np.log2([p ** p for p in X]) - np.log2([p ** p for p in (1 - X)])
  6. plt.plot(X, Y)
  8. plt.annotate('max value: 1', xy=(0.5, 1), 
  9.             xytext=(0.3, 0.3),
  10.             fontsize=16,
  11.             arrowprops=dict(arrowstyle='->'))

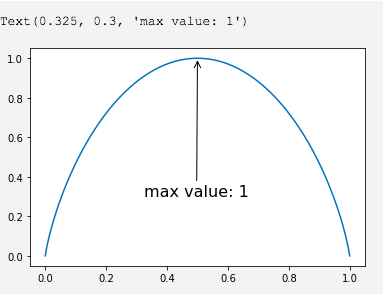
二元分类问题.png

我们动笔计算一下，也是如此

  1. X = [0.5, 0.5]
  2. Y = -np.log2([p ** p for p in X])
  3. print(Y.sum())                       # 0.9999999999999998   # 计算精度问题

针对二元分类问题，当p=0，或p=1时，熵的计算结果为0；也就是说某个事件百分之百发生，或百分之百不发生，那自然是没有什么不确定性了。当p=0.5时，H(p)=1，熵取值最大，随机变量不确定性最大。

条件熵

条件熵.png

信息增益定义

在引入概念之前，我们先考虑一个问题？假设我们选取了某个特征，并且根据该特征对数据集进行了划分，产生了多个子集，每个子集都可以计算出一个熵的值，那所有子集的熵的和（其实就是条件熵）是越大越好还是越小越好呢？换言之，是不是所有子集的熵的和越大，就说明我们选取的特征越好呢？

答案：不是的。所有子集的熵的和越大，说明这样划分导致的结果是不确定性越大（纯度越差），前面我们说过，我们希望划分后的子集能尽可能的被正确归类（纯度高），所以我们希望如果按照某个特定的特征来划分数据集，那划分后的结果数据集熵的总和是越小越好。

划分前熵的总和 - 划分后熵的总和（其实就是条件熵） = 信息增益

信息增益1.png

这里举一个例子：假设我们数据集中有20条样本，其中有10条样本属于类别C，另外10条样本属于类别C。每条样本有顾客ID，性别（男，女），车型（家用，运动，豪华），衬衣尺码（小，中，大，加大）这四个特征。

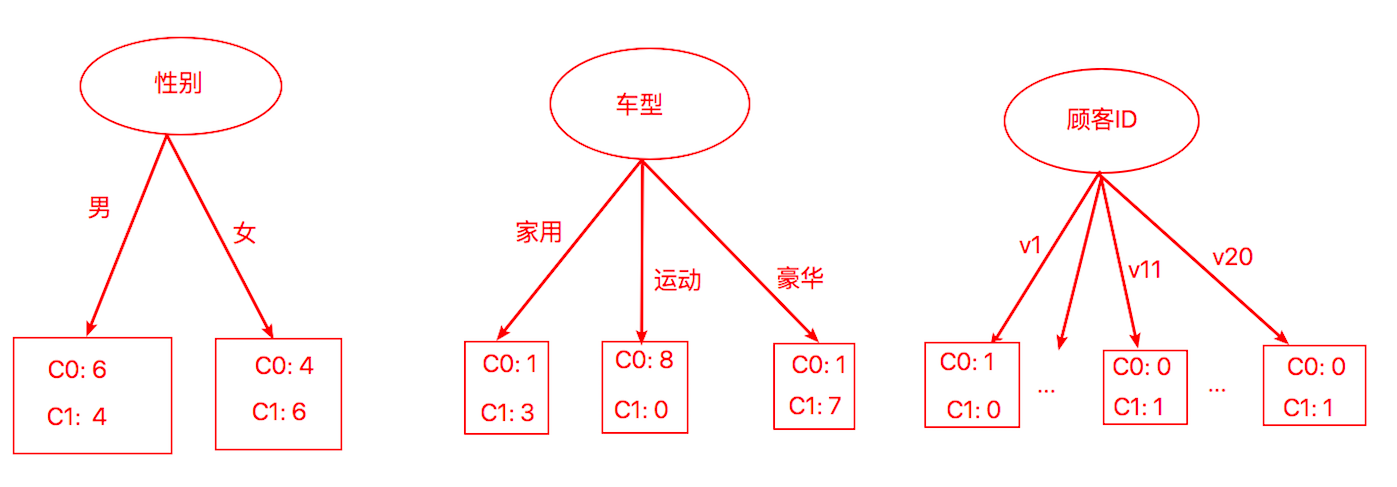
划分.png

我们来计算一下划分后的熵的总和（按照我们之前的条件熵的公式）

  1. # 按性别划分
  2. X1 = [0.6, 0.4]
  3. Y1 = -np.log2([p ** p for p in X1])
  4. X2 = [0.4, 0.6]
  5. Y2 = -np.log2([p ** p for p in X2])
  6. entropy = (10 / 20) * Y1.sum() + (10 / 20) * Y2.sum()
  7. print(entropy)          # 0.9709505944546688
  9. # 按车型划分
  10. X1 = [0.25, 0.75]
  11. Y1 = -np.log2([p ** p for p in X1])
  12. X2 = [1, 0]
  13. Y2 = -np.log2([p ** p for p in X2])
  14. X3 = [1/7, 6/7]
  15. Y3 = -np.log2([p ** p for p in X3])
  16. entropy = (4 / 20) * Y1.sum() + (8 / 20) * Y2.sum() + (8 / 20) * Y3.sum()
  17. print(entropy)          # 0.39892473632475756

很明显，按照车型这个特征来划分数据集，划分结果的条件熵值最小，不确定性低（纯度高）效果好。

选择最佳划分的度量通常是根据划分后子女结点不纯性（不确定性）的程度。不纯的程度越低（即很纯，即不确定性小），类分布就越倾斜（即是某一个特定类别的概率越大，越有可能被正确分类）

信息增益算法

信息增益算法.png

其实我们上面的计算过程，做的就是第二步的计算。这里就不多赘述了。条件熵的值最小，也就意味着信息增益的值最大。信息增益的值最大，说明我们选取的特征最优。

信息增益比

之前，我们在按特征划分20条样本时，并没有计算按照顾客Id去划分的情况。我们在这里算一下：

  1. # 按顾客ID进行划分（每个顾客属于特定类别，且总样本中类分布为0.5：0.5）
  2. X1 = [1, 0]
  3. Y1 = -np.log2([p ** p for p in X1])
  4. X2 = [0, 1]
  5. Y2 = -np.log2([p ** p for p in X2])
  6. entropy = (1 / 20) * Y1.sum() * 10 + (1 / 20) * Y2.sum() * 10
  7. print(entropy)          # 0 （有点极端了）

毫无疑问，这种情况下，划分后的条件熵值最小，信息增益最大，那我们为什么不选择这个顾客ID作为最优特征呢？因为与每个划分相关联的记录太少，以致不能作出可靠的预测。

解决该问题的策略有两种：第一种策略是限制测试条件只能是二元划分，CART这样的决策树算法采用的就是这种策略；另一种策略是修改评估划分的标准，把属性测试条件产生的输出数也考虑进去。例如，决策树算法C4.5采用作为增益率（gain ratio）的划分标准来评估划分。

信息增益比.png

如果某个特征产生了大量的划分，这会使得H(D)特别大，从而降低了信息增益比。

树的生成

常见的决策树算法

决策树概况.png

ID3算法

ID3算法.png

这里具体来解释一下这个算法，假设特征集A包含四个特征（a, b, c, d）, 阈值设置为0.5 （根据自己对算法和业务的理解，主观设置）

关于第一点：属于特殊情况，该数据集下所有的样本数据都有相同的类别，直接归为叶子节点了。（单节点树）

关于第二点：也属于特殊情况，已经没有可供选择的特征了，将该数据集下占比最多的类别作为类标号。（单节点树）

关于第三点：假设我们计算最大信息增益对应的特征为特征a，则在这里A就为a。

关于第四点：也属于特殊情况，假设我们计算出特征c对应信息增益为0.3，小于我们设置的阈值0.5，则置该数据集下占比最多的类别作为类标号。（单节点树）

关于第五点：假设我们基于特征a，划分成了3个子集，分别记为D,D,D，则将每个子集中占比最多的类别作为类标号。

关于第六点：前面我们基于特征a，划分成了3个子集，分别是D,D,D，这里以D为训练集，以{b, c, d}为特征集，递归调用1-5。

以前面的贷款数据为例，我们来实例应用一下ID3算法

首先，依次计算各个特征的信息增益

  1. # 计算初始熵的总和
  2. X = [6/15, 9/15]
  3. Y = -np.log2([p ** p for p in X])
  4. H = round(Y.sum(), 3)               
  5. print(H)                            # 0.971
  7. # 特征 年龄 （青年，中年，老年）（A1）
  8. X1 = [2/5, 3/5]
  9. Y1 = -np.log2([p ** p for p in X1])
  10. X2 = [3/5, 2/5]
  11. Y2 = -np.log2([p ** p for p in X2])
  12. X3 = [4/5, 1/5]
  13. Y3 = -np.log2([p ** p for p in X3])
  14. entropy = (5 / 15) * Y1.sum() + (5 / 15) * Y2.sum() + (5 / 15) * Y3.sum()
  15. gi = round(H - entropy, 3)          
  16. print(gi)                           # 0.083
  18. # 特征 有工作 （是，否）（A2）
  19. X1 = [5/5, 0/5]
  20. Y1 = -np.log2([p ** p for p in X1])
  21. X2 = [4/10, 6/10]
  22. Y2 = -np.log2([p ** p for p in X2])
  23. entropy = (5 / 15) * Y1.sum() + (10 / 15) * Y2.sum()
  24. gi = round(H - entropy, 3)          
  25. print(gi)                           # 0.324
  27. # 特征 有房子 （是，否）（A3）
  28. X1 = [6/6, 0/6]
  29. Y1 = -np.log2([p ** p for p in X1])
  30. X2 = [3/9, 6/9]
  31. Y2 = -np.log2([p ** p for p in X2])
  32. entropy = (6 / 15) * Y1.sum() + (9 / 15) * Y2.sum()
  33. gi = round(H - entropy, 3)          
  34. print(gi)                           # 0.42
  36. # 特征 信贷情况 （一般，好，非常好）（A4）
  37. X1 = [1/5, 4/5]
  38. Y1 = -np.log2([p ** p for p in X1])
  39. X2 = [4/6, 2/6]
  40. Y2 = -np.log2([p ** p for p in X2])
  41. X3 = [4/4, 0/4]
  42. Y3 = -np.log2([p ** p for p in X3])
  43. entropy = (5 / 15) * Y1.sum() + (6 / 15) * Y2.sum() + (4 / 15) * Y3.sum()
  44. gi = round(H - entropy, 3)          
  45. print(gi)                           # 0.363

观察数据可知，是否有房子这个特征的信息增益是最大的，因此，我们选取房子作为当前条件下的最优特征。

然后，我们构建基于是否有房子该特征的决策树，并对子节点作类标记。

接下来，剥离房子这个特征后，还有三个特征，再次依次计算它们各自的信息增益，这里只计算了年龄这个特征作为示例。

  1. X = [3/9, 6/9]
  2. Y = -np.log2([p ** p for p in X])
  3. H = round(Y.sum(), 3)               
  4. print(H)                           # 0.918 
  6. # 特征 年龄 （青年，中年，老年）
  7. X1 = [1/4, 3/4]
  8. Y1 = -np.log2([p ** p for p in X1])
  9. X2 = [0/2, 2/2]
  10. Y2 = -np.log2([p ** p for p in X2])
  11. X3 = [2/3, 1/3]
  12. Y3 = -np.log2([p ** p for p in X3])
  13. entropy = (4 / 9) * Y1.sum() + (2 / 9) * Y2.sum() + (3 / 9) * Y3.sum()
  14. gi = round(H - entropy, 3)          
  15. print(gi)                           # 0.251

ID3实例.png

C4.5算法

C4.5算法改进.png

这里想对C4.5的连续特征离散化作一个解释：假设我们数据集中有一列特征是身高，共20个样本，排好序之后，为161，162，….，180。取相邻两个样本的均值，于是就产生了19个划分点，为161.5，162.5，….，169.5，接下来我们分别计算这19个划分点的信息增益，以162.5举例来说，小于162.5的划分为一个子集，大于162.5的划分为另一个子集，划分后的子集中样本可能都属于同一类别，也可能属于不同类别。这样就可以计算以162.5为划分的信息增益了。划分点逐个计算之后，我们选取信息增益最大的划分点作为最终的二元离散分类点。（只想吐槽一句，计算量好多）

C4.5算法步骤.png

CART

CART引入

Classification And Regression Tree（分类回归树）

cart1.png

为什么说CART与C4.5非常类似，因为它们都要选取最佳分割点，但C4.5是只支持分类模型的。

基尼系数

基尼系数.png

关于第一个方框中的公式，我们想一想，K个类别的概率总和是不是就等于1。（基于总共K个类别的前提下）

可以手动计算一下，1 - (p + (1 - p)) = 2p(1 - p) ，看一下图形，在0~1范围内，针对二分类问题，p为0或1时，基尼系数最小，取值为0。

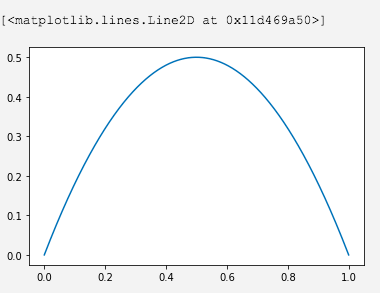
二次方程.png

基尼系数2.png

基尼系数前面的是数量之比

回忆一下，C4.5是基于排序后临近两个样本的均值划分的，而这里是取了某个特征的不同值逐个划分的。

CART算法

cart算法.png

ID3 和 C4.5 都是特征与特征之间进行比较的；而CART算法则是对特征内部的不同取值之间作比较。

每个特征都可以计算出一个最佳切分点，所有特征的最佳切分点的基尼系数进行比较，就产生了最优特征。该特征下的最佳切分点就成为了当前条件下的最优切分点。

因为CART算法针对某个分割点，总是是或否两种选择，这也造就了它最显著的特征，产生的总是二叉树。

cart案例.png
A2和A3特征是是否有工作，是否有房子，我们会发现计算A2取值为有工作的基尼系数和取值为无工作的基尼系数是相同的（是二分类），也就是说针对这种只有2个取值的特征，只计算结果为“是”这种情况的基尼系数就可以了。

看一下第二轮对基尼系数的计算

  1. # 计算特征A1的基尼指数
  2. G(D2, A1=1) = 4/9 * (2 * 1/4 * 3/4) + 5/9 * (2 * 2/5 * 3/5) = 0.433
  3. G(D2, A1=2) = 2/9 * (2 * 0/2 * 2/2) + 7/9 * (2 * 3/7 * 4/7) = 0.381
  4. G(D2, A1=3) = 3/9 * (2 * 2/3 * 1/3) + 6/9 * (2 * 1/6 * 5/6) = 0.333
  6. # 计算特征A2的基尼指数
  7. G(D2, A2=1) = 3/9 * (2 * 3/3 * 0/3) + 6/9 * (2 * 0/6 * 6/6) = 0   # 不用再往下算了，取值为0，说明结果已经可以被正确分类了

常见面试问题

你对决策树算法了解多少？
ID3，C4.5，CART之间有什么区别和联系呢？

C4.5相对于ID3使用的是信息增益比，能够将连续特征离散化。

CART衡量的标准是基尼系数，而且构建的最终结果是二叉树。它不仅要选取最优分类特征，还要选取最优切分点。