多元线性回归(P360)
多元线性回归同简单线性回归的整个流程没有太大差别,我们通过两个案例将整个的知识点串起来
案例分析:Butler运输公司
Butler运输公司面临的一个问题:管理人员希望估计司机每天行驶的时间。管理人员认为司机的行驶时间可能与每天运送货物行驶的里程以及运送货物的次数有关系。
Butler运输公司的数据:
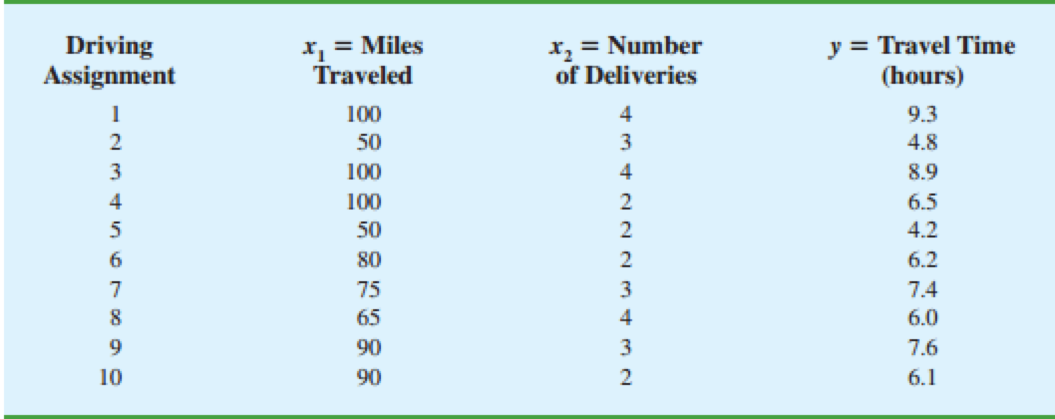
求解回归方程
我们使用Python程序来求解(求解的原理还是最小二乘法)
import pandas as pdfrom statsmodels.formula.api import olsdf = pd.read_csv("Butler.CSV")df_model = ols("Time ~ Miles + Deliveries", data=df).fit()print(df_model.summary())
注意:在ols中第一个参数,我们使用加号来添加自变量。
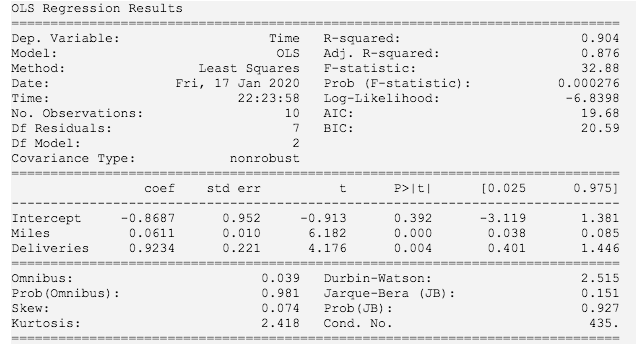
如上图所示,我们得到的回归方程是:
= 0.0611x + 0.9234x - 0.8687
我们看一下上图中有价值的信息都有哪些?Least Squares 表明是最小二乘法,右边给出了多元判定系数,修正的多元判定系数,F检验的临界值,概率值;中间有多元回归方程,标准差,t检验临界值,概率值,置信区间;下面有偏度等一些信息。
判定系数
假如我们只考虑了里程数这一个自变量,没有考虑到送货次数这个自变量,那么把它当成简单线性回归来处理时,我们同样会得到的一个判定系数,经过计算为0.664,而在两个自变量的情况下,被提升至了0.904,为了避免增加自变量影响到因变量中的变异性被估计的回归方程解释的百分比,我们提出用自变量的个数取修正判定系数,也就是上图中的Adj. R-squared,具体公式如下:(其中,n表示观测值的数目,p表示自变量的数目)
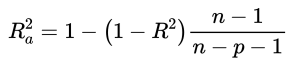
残差分析
在多元回归模型中,关于误差项 的假定与简单线性回归模型的那些假定类似。我们通过残差分析来确保我们的模型假定是有意义的,或者说至少没有被明显违背。
df['predicted'] = 0.0611 * df['Miles'] + 0.9234 * df['Deliveries'] - 0.8687df['residuals'] = df['Time'] - df['predicted']df.plot.scatter(x='predicted', y='residuals')
看下面我们作出来的残差图
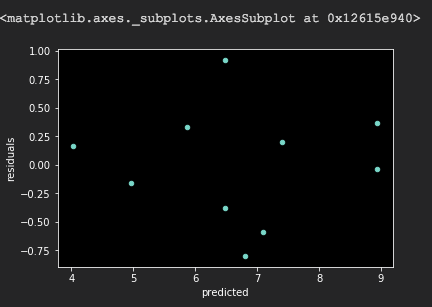
从图中我们可以看出,抛去异常值后,基本还是位于一个水平带附近的。
假设检验
F检验用于确定在因变量和所有自变量之间是否存在一个显著的关系,我们把F检验称为总体的显著性检验。
假设有10个自变量,那么F检验检验的是这10个自变量是否同时为0的情况。
如果F检验已经表明了模型总体的显著性,那么t检验用来确定每一个单个的自变量是否为一个显著的自变量。对模型中的每一个单个的自变量,都要单独地进行 t 检验,我们把每一个这样的t检验都称为单个的显著性检验。
在多元线性回归中,进行 t 检验的前提是,模型已经进行了F检验,且表明了总体的显著性。
总体显著性的F检验

放一个F分布的图(有个直观印象)
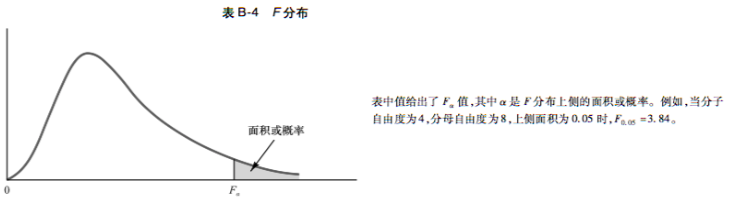
原假设:β = β = 0
备择假设:至少有一个参数不等于0
从我们之前程序的输出结果可以看到,F统计量为32.88,对应的p-value为0.000276小于显著性水平0.01,所以我们应该拒绝原假设。得出结论:每天行驶的时间 y 和每天运送货物的行驶里程x,运行货物的次数x 这两个自变量之间存在一个显著关系。
单个参数的t检验
**
我们有两个自变量,因此作2次 t 检验,从前面程序的输出结果,我们看到两次 t 检验对应p-value值一个是0.000,一个是0.004,均小于显著性水平0.01。因此我们得出拒绝原假设(H: β = 0 和 H: β = 0)的结论。
案例分析:水过滤系统
约翰逊过滤股份有限公司想要预估每次帮客户维修所需要的时间,管理人员认为维修时间依赖于两个因素:一个是从最近一次维修服务至今水过滤系统已经使用的时间,另一个是需要维修的故障类型。
约翰逊过滤公司的数据
**
我们定义如下的变量: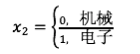
在回归分析中, 被称为虚拟变量或指标变量(哑变量),我们可以把多元回归模型写成如下形式:
我尝试定义该虚拟变量为其它的随机数(比如3和1,5和10),最后得到的回归方程是截然不同的,截距不同。
我们将数据集中分类变量的值用0和1替代之后,使用程序来求解。
Python 程序求解
import pandas as pdfrom statsmodels.formula.api import olsdf = pd.read_csv("Johnson.csv")df_model = ols("Time ~ Months + C(Type)", data=df).fit()print(df_model.summary())
这里解释一下ols(ordinary least squares)方法参数中C的含义,C是分类的意思,表示后面括号中对应的那一列变量为分类变量。在这个代码块中,研究Time(维修时间)与Months(月份)和Type(类型)之间的线性关系,其中Type这一列对应的数值为分类变量。
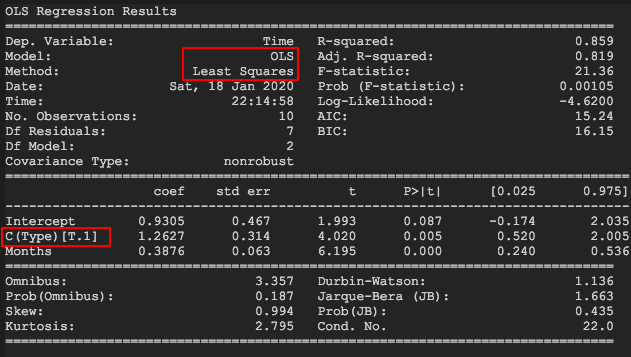
注意图中圈红框的地方,一个表明这个求解原理依旧是最小二乘法,另一个表明该分类变量取值为1时对应的系数。我们可以观察到:在显著性水平0.05下,与F检验相关联的P-值是0.001,这就表明回归关系是显著的;t 检验部分表明,两个自变量在统计上都是显著的;修正的判定系数表明估计的回归方程很好地解释了维修时间的变异性。
结果解读

满足特定条件下的期望值,这里我想既然就一个分类值,于是我只考虑机械类型的维修数据,得到了一个简单线性回归;只考虑电子类型的维修数据,得到了一个简单线性回归;发现和通过分类来求解线性回归的结果是不同的。可能是由于我只考虑了部分数据的原因。
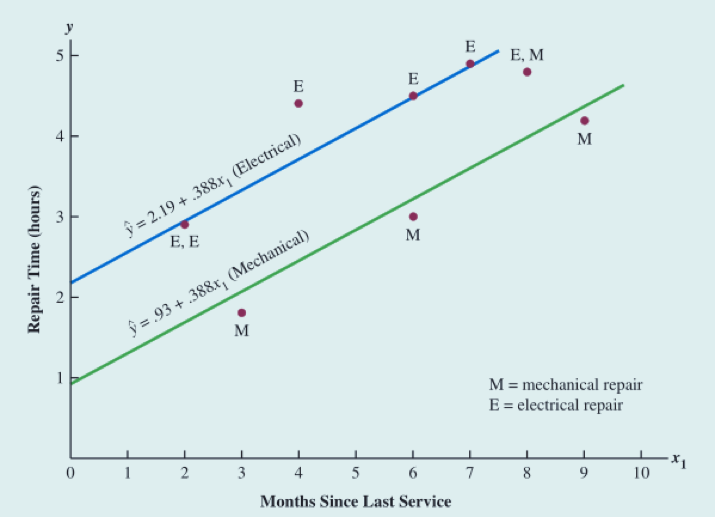
最终估计的多元回归方程:
- 机械类故障:
- 电子类故障:
我们得到了两个估计的回归方程。因为 b = 1.263(2.193 - 0.93),可得知:电子类型故障的维修时间要比机械类型故障的维修时间多用了1.263个小时。
复杂分类变量
如果一个分类变量有超过2个值呢?我们该如何处理?
销售地区A、B、C三个值,因此我们需要定义3-1=2个虚拟变量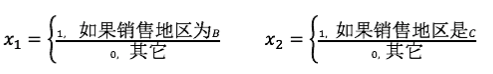
表格形式如下所示:

之所以定义k-1个虚拟变量,是因为其中一个水平我们可以用全部取值为0来表示,剩下的k-1个每个虚拟变量一个咯。遗留一个思考题:如果一个多元线性回归中,有2个分类变量,就比如在这里,一个是销售地区(A,B,C),一个是维修水平(电子,机械),我们应该定义几个虚拟变量呢?(应该定义5个,2 * 3 - 1)

