简单线性回归

简单线性回归模型（P318）

管理决策经常取决于对两个或多个变量之间关系的分析：

• 把预测的变量称为因变量
• 把用来预测因变量的一个或多个变量成为自变量
• 只包括一个自变量和一个因变量，二者之间的关系可以用一条直线近似表示，这种回归分析被称为简单线性回归

回归模型和回归方程

描述y如何依赖于x和误差项的方程称为回归模型

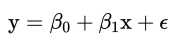
式中β，β被称为模型的参数（注意：是总体的参数）；ϵ是一个随机变量，被称为模型的误差项。

误差项说明了包含在y里，但不能被x和y之间的线性关系解释的变异性。

描述y的期望值E(y)如何依赖于x的方程称为回归方程

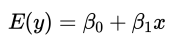
估计的回归方程

描述y的期望值E(y)如何依赖于x的方程称为回归方程

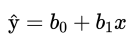
案例理解

Armand披萨店在美国都开在大学附近，其管理人员认为连锁店的销售收入y与学生人数x是正相关的。我们将会利用回归分析，求出一个能说明因变量y是如何依赖自变量x的方程。在案例中，总体是由所有的Armand披萨店连锁组成的。对于总体中的每一个连锁店，都有一个学生值x和一个对应的季度销售收入y值。

Armand披萨店的总体还可以视为由若干个子总体组成的集合，每一个子总体都对应一个不同的x值：一个子总体由8000名学生的校园附近的Armand披萨店组成的；一个子总体由9000名学生的校园附近的Armand披萨店组成的；每个子总体都会对应一个y值的分布，y值的每一个分布都有它自己的平均值或期望值。

这里为什么说y值的每一个分布都有它自己的平均值或期望值。因为具体来讲，8000名学生的校园可能有多个，而每一个都对应着一个y值，也就是说，一个子总体对应着一个x值，却可能对应多个y值，因此就存在平均值了。这也解释了为什么在简单线性回归方程中，等号左边取的是y值的平均值或者说是期望值。

估计步骤

1. 如果总体参数β，β已知，那么对于一个给定的x值，我们就能利用公式：简单线性回归方程，计算y的平均值；在实际中，β，β都是未知的，我们必须使用样本统计量b，b作为总体参数β，β的估计量。
2. b是截距，b是斜率，我们将利用最小二乘法来求解这两个值。
3. 我们不能把回归分析看作在变量之间建立一个因果关系的过程。回归分析只能表明变量时如何彼此联系在一起的。

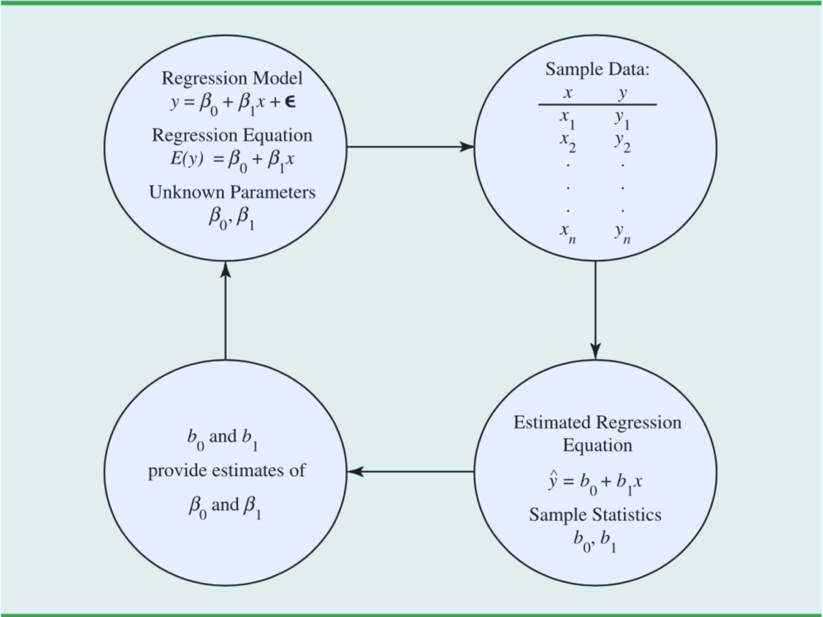
这四个循环的图可以说把内容概括得很全了，因为我们没办法知道总体参数（没办法拿到所有的数据），因此通过样本数据来计算样本统计量，在这里是斜率和截距，也就是总体参数的点估计量。注意，对于一个给定x值，也是E(y)的一个点估计。整个的过程是循环的，如果总体参数不知道，那就抽取样本计算斜率截距进行估计呗。

最小二乘法则（P320）

先介绍几个符号的含义：

• x: 第i个观测值（第i家连锁店的学生人数）
• y: 第i个观测值（第i家连锁店的销售收入）

下表统计了披萨店和学生人数，销量的数据，绘制散点图看一下大致的趋势。（Population的单位为1千人，Sales的单位为1000美元）

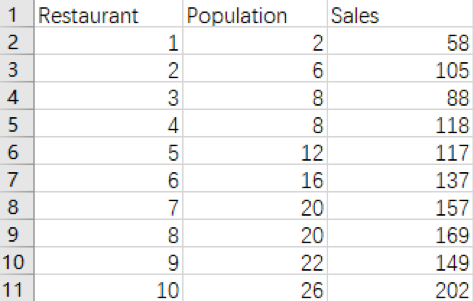
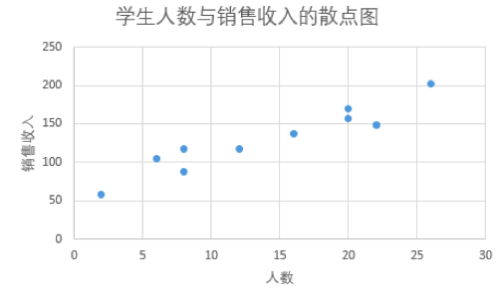
似乎人数越多，销售收入越高，它们之间可以用一条直线近似的表示。

最小二乘法

为了使估计的回归直线能对样本数据有一个好的拟合，我们希望销售收入的观测值与销售收入的预测值之间的差要小。

最小二乘法利用样本数据，通过使因变量的观测值 y 与因变量的预测值 之间的差的平方和达到最小的方法求得b，b的值。

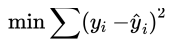
公式中 y 对于第𝑖次观测因变量的观测值； 为对于第𝑖次观测因变量的预测值。

案例应用

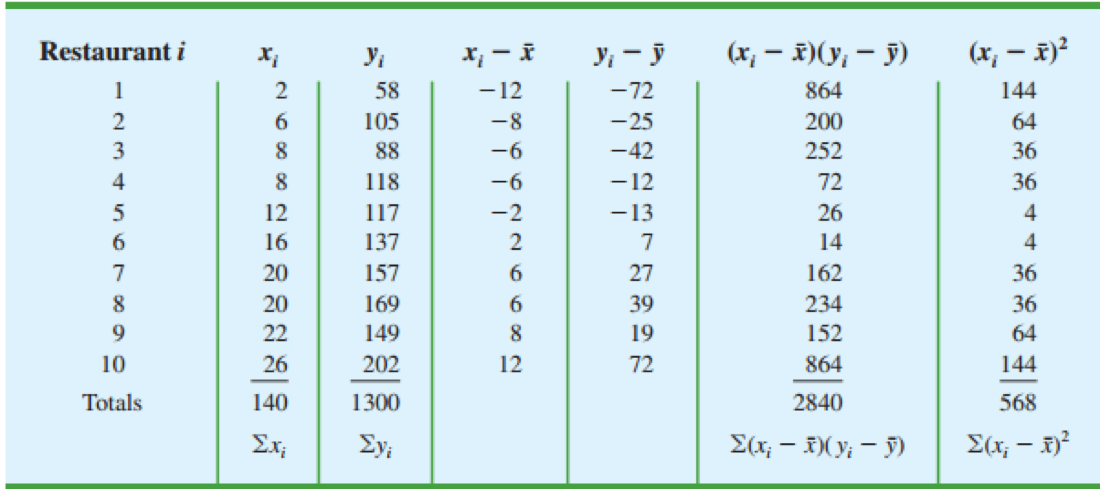
计算x的平均数为 140/10 = 14 ；y的平均数为 1300/10 = 130

利用公式便可求解得出 b = 60 ；b = 5

估计的回归方程： = 60 + 5x

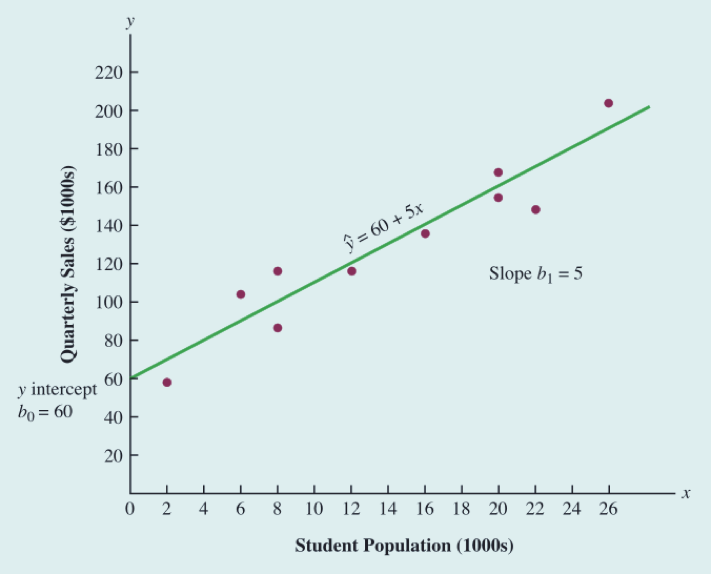
回归方程的斜率是正的，表明随着学生人数的增加，Armand披萨店的季度销售收入也增加。

更进一步的结论为学生人数每增加一千人，销售收入增加五千美元。

判定系数（P325）

判定系数为估计的回归方程提供了一个拟合优度的度量。

误差平方和

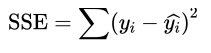
观测值减去预测值的平方和

观测值在回归方程附近聚集程度的度量

总的平方和

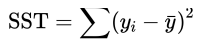
观测值减去平均值的平方和（注意：这里指的是所有观测值的平均值，也可以叫离差平方和）

可以看作是观测值在 y = 直线附近聚集程度的度量

回归平方和

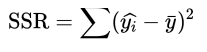
预测值减去平均值的平方和（注意：这里指的是所有观测值的平均值）

判定系数

如何利用这三个平方和为估计的回归方程给出一个拟合优度的度量呢？

• 如果因变量的每一个值 y 都刚好落在估计的回归线上，那么估计的回归方程将给出一个完全的拟合。这时候，对于每一个观测值, y − 都等于0，从而导致SSE=0.
• SST = SSR + SSE，对于一个完全拟合，SSR必须等于SST，也就是SSR / SST = 1.
• 值SSR/SST将在0到1之间取值，这个比值被称为判定系数

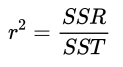
• 回到披萨店的案例中，判定系数为 14200 / 15730 = 0.9027
• 我们把 r 理解为总平方和中能被估计的回归方程解释的百分比。
• 在用估计的回归方程去预测销售收入时，我们能断定总平方和的90.27%能被估计的回归方程所解释。
• 换句话说：销售收入变异性的90.27%能被学生人数和销售收入之间的线性关系所解释。
• 这里的变异性指的就是观测值（实际值）与平均值（期望）的差值

样本相关系数

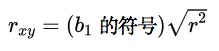
• 关于Armand披萨店中的样本相关系数： +0.9501 表示的是x和y之间存在着一个强的正向的线性关系
• 在两变量之间的存在一个线性关系的情况下，判定系数和样本相关系数都给出了他们之间线性关系强度的度量
• 样本相关系数的适用范围被限制在两变量之间存在线性关系的情况，但是判定系数对非线性关系以及有两个以上的自变量的相关关系都适用。因此判定系数有着更广泛的适应范围

模型的假定（P329）

判定系数 𝑟 即使较大，我们也需要对假定模型的合理性做出进一步的分析（是否符合统计学上的一些假定）

确定是否合理的一个步骤：是要对变量之间关系的显著性进行检验

而进行显著性检验的前提是误差项要满足一些条件，即下面的四条假定（层层相扣的）

1, 误差项 𝜀 是一个平均值或期望值为0的随机变量，即 𝐸(𝜀) = 0

我们期望我们估计出来的模型是没有误差的，是理想状态下的。也就是说我们估计出来的β, β就等于真实的值，因为有 β 和 β 是常数，所以 E(β) = β 和 E(β) = β ，每一个x值对应着一个误差，所有误差值的期望应该为0。

2, 对所有的x值，𝜀 的方差都是相同的。我们用 σ 表示 𝜀 的方差

方差是用来干嘛的？用来衡量变异程度的对吧，对于同一组数，都加上一个常数或减去一个常数，它们总体的方差是不会发生变化的，在这个假设中，x充当常数，y是关于 𝜀 的函数，所以对于所有的x值，y的方差都是相等的。

3, 𝜀的值是相互独立的

样本与样本之间是相互独立的，（比如第一家披萨店的销量和第二家披萨店的销量是没关系的），那么每个样本的误差也是相互独立的。

4, 对所有特定的x值，误差项𝜀是一个正态分布的随机变量

y是关于误差项的线性函数，从前面的简单线性回归模型可以看出来，既然误差项是一个正态分布的随机变量了，x当作常数，y又是线性的，那么y也是一个正态分布的随机变量了。

对于所有的x，误差的方差（变异程度）相同；对于所有特定的x（比如x=20），误差是一个正态分布的随机变量；关于这两点，这个图片给出了很形象的解释。

显著性检验（P330）

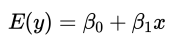
对于上面的简单线性回归方程，如果 β 的值是0，那么y的平均值或者期望值不依赖于x的值，因此我们得出的结论是两变量x和y之间不存在线性关系。我们必须使用一个假设检验来判定 β 的值是否等于0，从而检验出两个变量之间是否存在线性关系。（有点像做完了一道数学题，然后反过来推导验证一下）

总体方差 𝝈 的估计

• 𝜖 的方差 𝝈 也是因变量y的值关于回归直线的方差。（参考下面的公式定义理解）
• 残差平方和SSE是实际观测值关于估计的回归线变异性的度量
• 利用SSE除以它自己的自由度，得到均方误差MSE，均方误差给出了 𝝈 的一个估计量
• 统计学家已经证明，为了计算SSE，必须估计两个参数β，β，所以SSE的自由度是n-2。（n为样本容量，2为未知参数的个数）

均方误差MSE（𝝈的估计量）

估计的标准误差

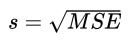
披萨店的案列中，s = 1530 / 8 = 191.25, s = 13.829

注意：这里之所以会介绍估计的标准误差，首先第一点：我们没办法知道误差项的总体标准差，只能通过点估计量来估计，第二点：后面在计算 b 的检验统计量时会用到这个估计的标准误差

这里提供了一种估计总体标准差 𝝈 的方式（估计的标准误差）；后面的F分布会提供另外一种估计方式

你看这里的总体方差的估计公式，像不像之前学习过的方差的计算公式，与平均数差值的平方和 / (n - 1)，之前的自由度为 n - 1，此时的自由度为n - 2。

t 检验

构建关于 β 的双侧检验

• H: β = 0 H: β ≠ 0
• 如果 H 被拒绝，我们将会得到 β ≠ 0的结论，于是证明了x与y之间存在一个统计上显著的关系；
• 如果 H 没有被拒绝，我们将没有充分的理由来断定x与y之间存在一个统计上显著的关系;

我们使用了不同的样本就会得出不同的估计的回归方程。比如披萨店的案列中，我们假设使用了另一批样本，我们得到的估计回归方程只能是和 = 60 + 5x 相似，但是不太可能完全一致。实际上，最小二乘估计量 b，b 是样本统计量，他们有着自己的抽样分布。（就如同样本均值符合正态分布一样，不同的样本会得到不同的 b，b，这一系列的值有着自己的分布）

在上面的图中，b 的期望值等于 β，所以 b 是 β 的无偏估计量（换句话说，b 这个样本统计量的平均值等于 β）

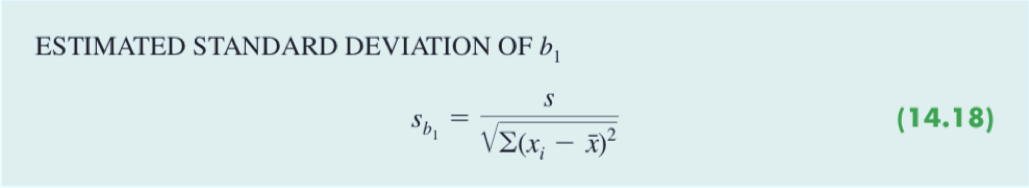
由于总体标准差 𝜎 是未知的，使用样本标准差。

计算过程

特别注意一下这里样本的检验统计量

我们回忆一下总体标准差已知，正态分布的样本均值检验统计量：(样本均值 - 总体均值) / 样本标准差；

总体标准差未知，t分布的样本均值检验统计量：(样本均值 - 总体均值) / 样本标准差；

没毛病，这里β的期望取值为0，只不过是这里样本标准差的计算方式发生了变化。

β 的置信区间

这里的 1.95 是 3.355 * 0.5803 得到的。（置信区间肯定与假设检验是有关系的，前面我们得出过结论）

在这个案例中，置信系数为0.99，也就是说有99%的概率落在这个置信区间内，1%的概率落在这个置信区间外。而 β = 0 显然不在置信区间内，而且 β = 0 的概率是小于0.01的，因此拒绝原假设。

连续变量的概率求解只与概率密度函数下方的面积有关。置信区间外所有的范围概率才占0.01，那么 β = 0 的概率肯定是小于0.01的。

F 检验

F检验被用来检验回归方程总体的显著关系，也就是说，假设有两个自变量，那么F检验检验的是 β = 0 同时 β = 0 的概率。而t分布依旧是单个单个进行检验的。

为什么说 β != 0 时，MSR是高估 𝝈 的？我们回到源头部分，SSE 是误差平方和，观测值与预测值差值的平方和，除以(n-2)后，就可以用来估计总体的方差，而且是理想的状态（无偏估计量）；而 SSR 是回归平方和，它度量的是预测值与样本均值的变异程度，也就是预测值在一条直线附近聚集程度的度量，这肯定会造成算出来的结果相对MSE特别大。

显著性解释

• 拒绝原假设 H: β = 0 并且得出变量x和y之间存在显著性关系的结论，并不意味着我们能得出变量x和y之间存在一个因果关系的结论。
• 我们仅仅是证实了变量x和y之间存在统计显著性关系，但这并不能让我们得出变量x和y之间存在线性关系的结论！我们仅仅能说明在x的样本观测值范围内，x和y是相关的。而且这个线性关系只是在x的样本观测值范围内，解释了y的变异性的显著部分。(很严谨)

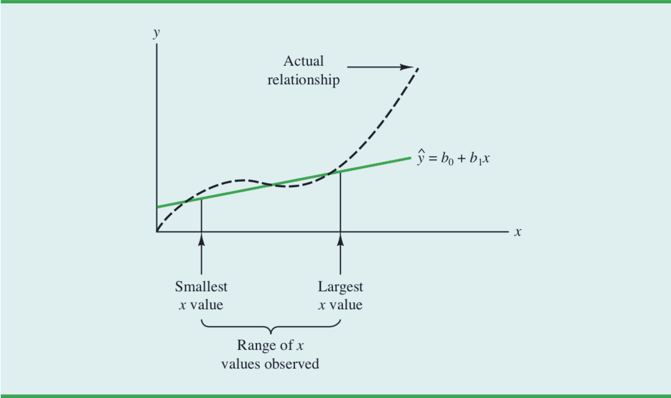
我们利用估计的回归方程对于x的样本观测值范围以内的x值进行预测，应该是完全有把握的。但是超过这一范就需要十分谨慎！

Python 程序求解回归

需要安装 statsmodels 库，使用pip install命令进行安装。

import pandas as pd
from statsmodels.formula.api import ols
df = pd.read_csv("Armand's.CSV")
# fit方法训练模型
df_model = ols("Sales ~ Population", data=df).fit()
print(df_model.summary())

这里我想解释一下 ols 的第一个参数表示是一个公式，其中Sales是y，是因变量，Population是x，是自变量，中间用波浪线隔开（键盘上数字1左边的那个）

看一下结果：

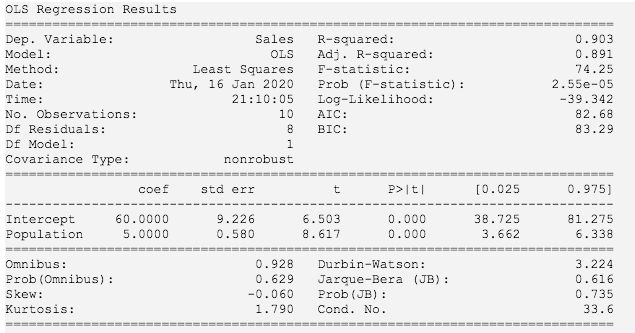
其中Intercept表示截距，在这里可以视为 b，Population在这里可以视为斜率 b。如果对其中的某些数值不太理解，我们可以对比下面Excel求解回归的输出。

Excel 求解回归

具体的步骤这里就不详细列出了。（如果忘记，可以在Excel帮助里搜索数据分析，查看在线文档）

看一下结果（同样应用Armand’s.CSV数据集）：

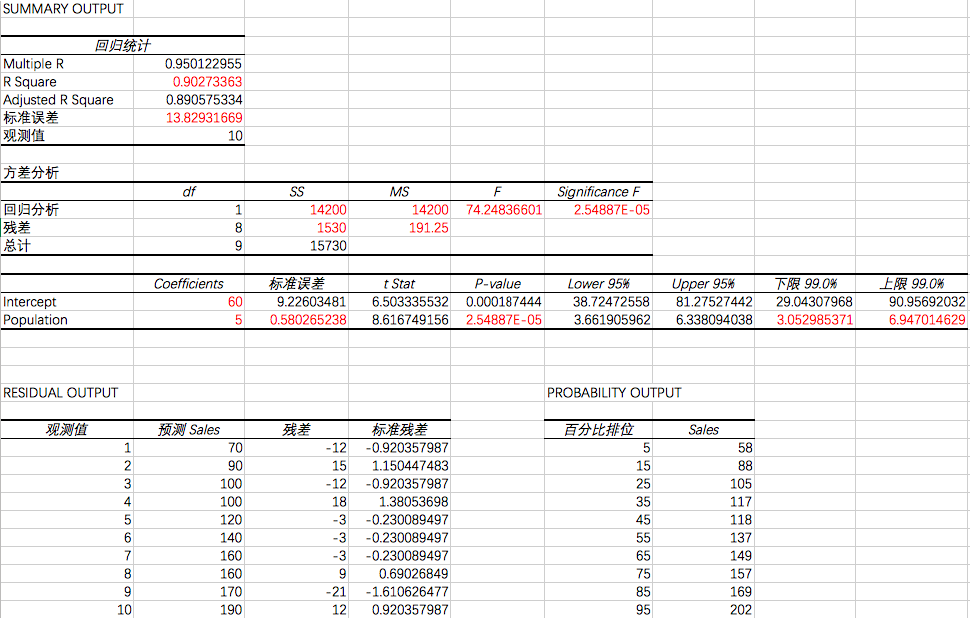
我们可以对比下，标红的这些数值，是不是和我们之前求解的数值都是相等的，包括SSR, SSE, SST, MSR, MSE 还有假设检验和置信区间。

残差分析（P342）

• 残差分析的目的是为了证实模型的假定
• 这些假定对于显著性检验、置信区间估计都提供了理论上的依据。如果关于误差项 𝜀 的假定显得不那么可靠，那么有关回归分析的结果可能会站不住脚
• 残差提供了有关误差项 𝜀 的重要信息。因此，残差分析是确定误差项𝜀的假定是否成立的重要步骤
• 残差分析都是在对残差图形仔细考察的基础上完成的（有一定的主观意愿）

第 𝒊 次观测的残差: y -

• y 代表因变量的观测值
• 代表因变量的预测值

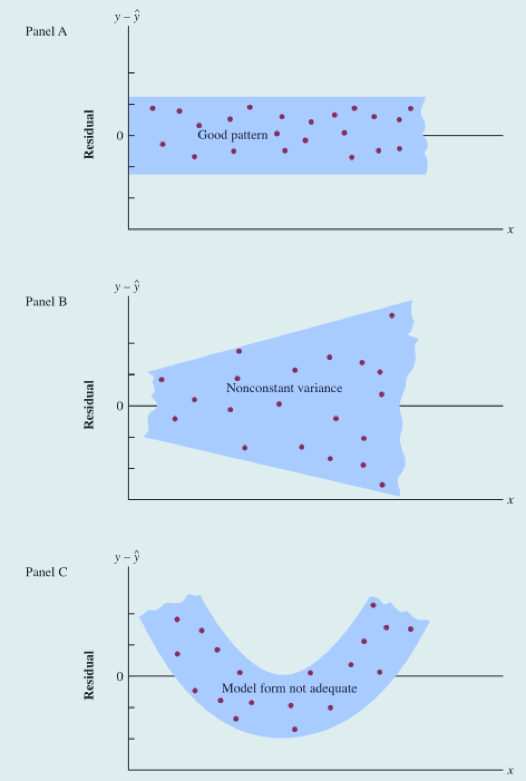
Armand的残差数据

关于 x 的残差

三种回归研究的残差图

残差图（residual plot）：横轴表示自变量的值，纵轴表示对应的残差值。

• Panel A示意所有的散点都落在一条水平带中间。
• Panel B示意我们违背了残差有一个相同的常数方差的假定。
• Panel C示意回归模型不恰当

之前第二条模型假定是：对于所有的x值，误差项的方差是相同的。也即是说，对于所有的x值，误差项的变异程度是相同的。当x等于1时，和x=10时残差的变异程度应该是相同的。反映在残差图上，就是位于一条水平带中间。

案例的残差图

残差的分布接近于Panel A。因此，我们的结论是残差图并没有提供足够的证据，使我们对Armand的回归模型所做的假定表示怀疑。

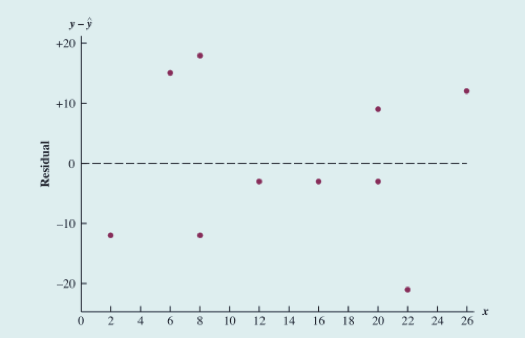
关于 残差图

• 的残差图与 x 的模式一致，我们无法对模型的假定产生怀疑。
• 对于多元回归分析，因为有一个以上的自变量，所以 的残差图更适用

标准化残差

第 i 个残差的标准差

标准化残差的计算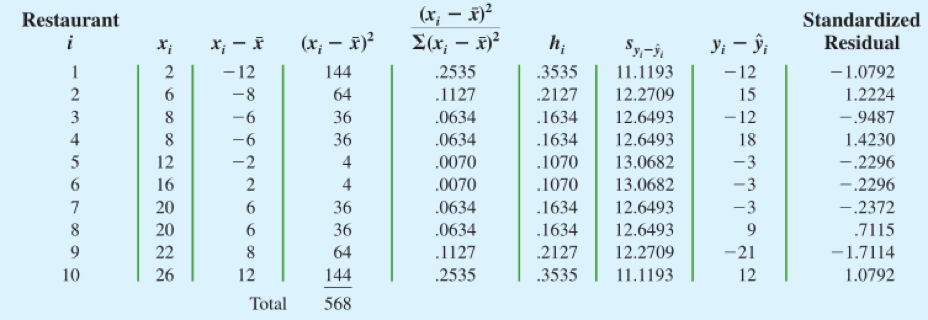


**第 𝒊 次观测的标准化残差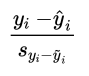


** 正常来讲，我们标准化一个随机变量是怎么做的？减去平均数，除以标准差。这里由于残差的平均值是零，于是每个残差只要简单地除以它的标准差，就得到了标准化残差。

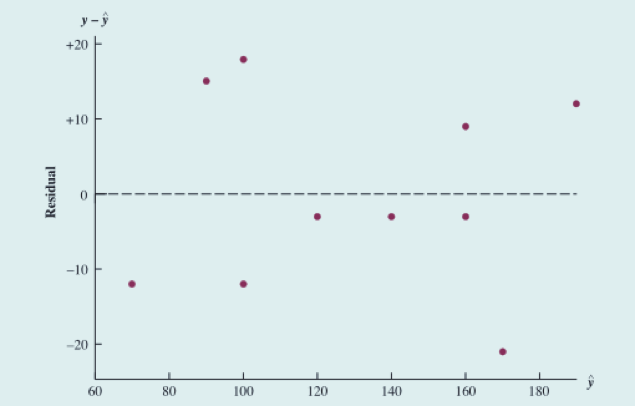
关于自变量x的标准化残差图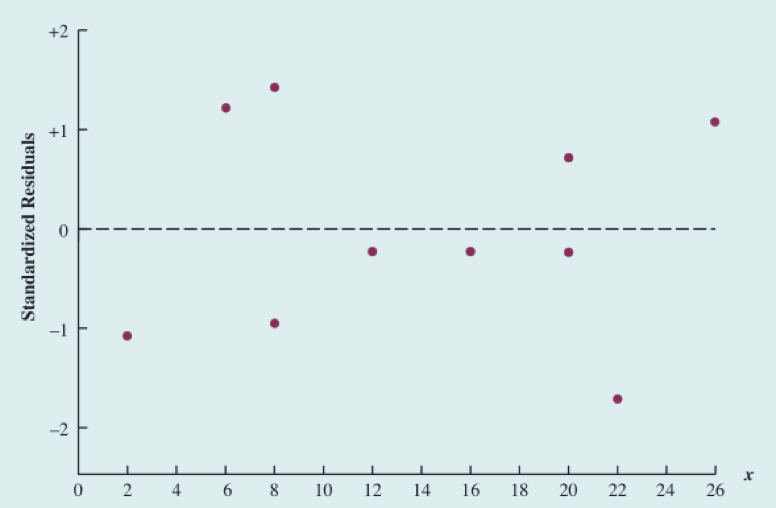



**标准化残差图能对随机误差项 𝜀 服从正态分布的假定提供一种直观的认识。

如果这一假定被满足，那么标准化残差分析分布看起来也应该服从一个标准正态分布。

看图可知，大约有95%标准化残差介于-2 ~ +2之间。

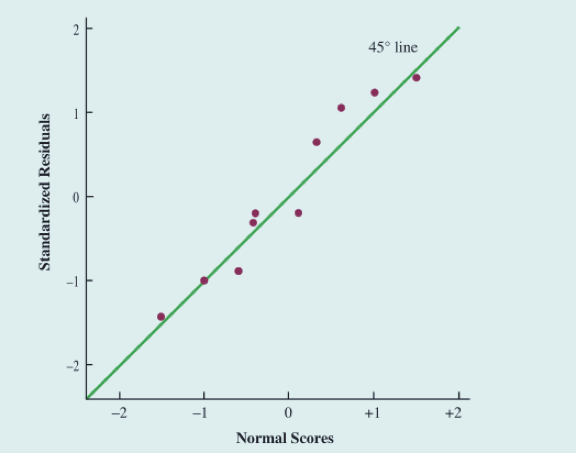
正态概率图

确定误差项 𝜀 服从正态分布的假设成立的另一个方法是正态概率图

什么是正态分数？

1. 从均值为0，标准差为1的标准正态概率分布的数据中随机抽取10个数值
2. 重复这一抽样多次，然后把每个样本中的数据进行排序
3. 选取每个样本中的最小值，组成一个随机变量，被称为一阶顺序统计量
4. 统计学家已经证明：来自标准正态概率分布的容量为10的样本，一阶顺序统计量的期望值为-1.55。这个期望值被称为正态分数
5. 一般的，如果数据集由n个观测值组成，那么就有n个顺序统计量和n个正态分数

Armand案例分析

• 对于Armand案例，我们将10个正态分数和10个排好顺序的标准化残差放在一起。如果正态性的假设被满足，那么最小的标准化残差应接近最小的正态分数，以此类推
• 横轴表示正态分数，纵轴表示标准残差。如果符合正态分布，那么这些点应该围绕在45度直线附近
• 从图中可以看出，随机误差项服从标准正态概率分布的假定是合理的

我们利用残差和正态概率图来证实一个回归模型的假定。如果我们的检查表明一个或几个假定是不可靠的，那么我们就应该考虑一个不同的回归模型或者一个数据变换。

证实回归模型的假定成立的主要方法是残差分析。即使没有发现假定被违背，但是这并不一定意味着模型将能给出一个好的预测。然而，如果有补充的统计检验支持显著性结论，并且有较大的判定系数，那么我们的模型就有一个比较好的预测。

也就是说一个简单线性模型合理有三点条件需要满足：

1. 模型的假定没有被违背（残差分析是ok的）
2. 可以得出显著性检验的结论（可以拒绝斜率等于0的假设）
3. 有一个较大的判定系数