logistic回归

回归定义及求解

定义描述

logistic regression 中文名翻译成逻辑斯蒂回归，而不是逻辑回归。（实际应用中还是很广泛的）

当因变量的值是两个离散值时，我们称这是一个二分类模型。最基础二分类模型就是logistic 回归。
**
案例：
Simmons商店正在使用的一种直接邮寄广告的促销手段。他们计划印刷5000份昂贵的彩色商品目录，并且每份商品目录还赠送一张商家优惠券。因为商品目录价格昂贵，所以Simmons只愿意将商品目录寄送给那些最有可能使用优惠券并购买商品的顾客。

根据客人的年消费支出与是否拥有Simmons信用卡两个特征，来计算顾客使用优惠券的概率。表格中记录了部分去年消费者的特征与是否使用优惠券的数据。

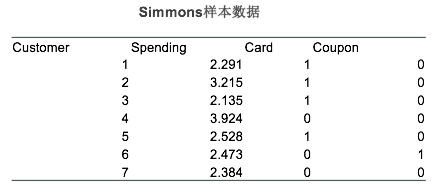
通常情况下，带有回归二字的模型基本都是线性模型，而且因变量（也叫响应变量）是连续的；但logistic回归比较特殊，虽然带有回归二字，但它的因变量为离散型变量。因为logistic回归与线性回归有着千丝万缕的关系。

如果因变量不是二分类，而是有2个以上的类别，logistic也能做，不过通常情况下，logistic回归最常用的场景就是二分类模型。

logistic回归与线性回归的区别就在于，线性回归的因变量是连续的，而logistic回归的因变量是离散的。

logistic回归方程

logistic回归方程由一个因变量和一个或一个以上的自变量组成。

logistic回归方程：

因变量的取值为1或0，那么E(y)给出的是在给定一组自变量值的情形下，有关y=1的概率。

logistic回中的E(y)被解释为概率：

注意：这里的自变量可以是连续型变量，也可以是离散型变量。也可以同时存在。

仔细观察这个回归方程，e是一个自然常数，e的指数是不是很像多元回归的线性方程。某种程度上解释了logistic回归和线性回归的关系。

从概率角度上进行理解，很重要。

为如果我们定义，那么logistic回归方程可以写成：

进一步转化，等号右边公式分子分母都除以 ，可得：

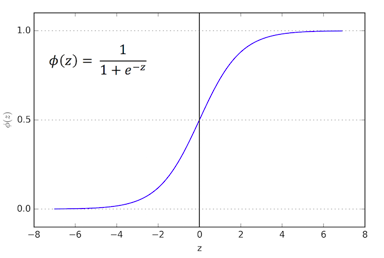
从这个图形中，我们可以看到E(y)的取值在0-1之间，这从理论上保证了logistic适合做概率模型；随着z值的增大，输出的结果也就越大，越来越接近1；在S曲线的中间阶段，值变化的速度很快，但是在两端趋于平稳缓和。

继续观察上面这个图形，有一条虚线，y = 0.5，这个是我们的阈值，阈值是我们用来区分类别的一个标准，比如最终我们计算出要预测样本的概率值大于0.5，则视为类别1，否则，则视为类别0。阈值也可以设置为其它值，根据实际业务需要。

估计logistic回归方程

logistic回归的求解通常使用的是凸优化理论的梯度法和牛顿法，手动计算很麻烦，也超出了课程范围。但是我们可以使用Python很方便的求解。

估计的logistic回归方程：

给出了y = 1的概率的估计。

案例求解

回到Simmons商店的例子。我们定义的变量如下所示：

于是，我们有两个自变量的logistic回归方程为：

import statsmodels.api as sm
import pandas as pd
df = pd.read_csv("Simmons.csv")
x = df[['Spending', 'Card']]
y = df['Coupon']
# 往自变量x中添加常数，并赋值给x
x = sm.add_constant(x)
model = sm.Logit(y, x).fit()
print(model.summary2())

执行

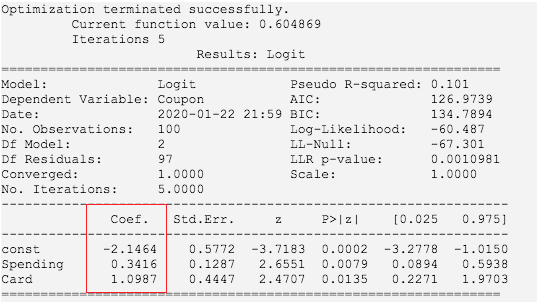
如果你注释掉给自变量添加常数的那行代码，会得到一个完全不同的输出。

主要看圈红框的部分，表示我们求解出来的参数。对总体参数进行估计，最终的logistic回归方程为：

根据这个结果，我们可以对新用户进行预估：假设一位顾客去年消费2000美元并且拥有信用卡，我们将=2，=1代入公式，得到： ，结论：他们使用优惠券的概率大约为0.19。

回归解释

机会比率计算

有利于一个事件发生的机会比：事件将要发生的概率与该事件将不会发生的概率比。
在自变量的一组特定值已知时，有利于事件 y = 1 发生的机会比计算公式：（有时候也叫优势比）

机会比率：度量了当一组自变量中只有一个自变量增加了一个单位时对机会比的影响。

将去年消费2000美元并且拥有信用卡的顾客，即=2，=1，使用优惠券的的机会比，与去年消费2000美元但是没有信用卡的顾客，即=2，=0，使用优惠券的的机会比进行比较。我们感兴趣的是解释自变量增加一个单位的影响。

估计的机会比率是

机会比率解释

去年消费支出为2000美元并且拥有Simmons信用卡的顾客使用优惠券的机会比，是去年消费支出为2000美元但没有Simmons信用卡的顾客使用优惠券的机会比的3倍。

其它的自变量取何值对于计算某一自变量的机会比率没有任何影响，即拥有Simmons信用卡的顾客使用优惠券的机会比，是没有拥有Simmons信用卡的顾客使用优惠券的机会比的3倍。

前者的机会比是后者机会比的3倍，并不代表在其他自变量相等条件下前者使用优惠券的概率是后者的3倍，代入公式求解一下就会发现并不是如此。机会比肯定是越大越好，越大表明该事件越有可能发生。

连续型自变量的估计的机会比率：
**
考虑的问题是：当自变量增加一个或者超过一个单位时机会比的变化情况。例如，去年消费支出为5000美元的顾客使用优惠券的估计的机会比，是去年消费支出为2000美元的顾客使用优惠券的估计的机会比的多少倍呢？

在一个变量的机会比率和它所对应的回归系数之间存在一个唯一的关系。在logistic回归方程中，每一个自变量都能表示如下形式：

即的估计的机会比率是： , 同样的的估计的机会比率是：

通过回归系数来求解机会比率，这种方式貌似简单许多。针对连续型变量的机会比率，指的是增加一个单位时的情况。即当一个自变量变化一个单位，而其他所有的自变量都保持不变时，一个自变量的机会比率描述了该自变量机会比的变化。

回到案例中：
**
去年消费支出为5000（=5）美元的顾客使用优惠券的估计的机会比，与去年消费支出为2000 （=2）美元的顾客使用优惠券的估计的机会比进行进行比较。这种情形下，c=5-3=2，对应的机会比率是：

我们可以得到如下的结论：去年消费支出为5000美元的顾客使用优惠券的估计的机会比，是去年消费支出为2000美元的顾客使用优惠券的估计的机会比的2.79倍；换句话说，对于一个去年消费支持增加3000美元的顾客而言，使用优惠券的估计的机会比率是2.79。（这里5 - 2 = 3相当于是增加了3个单位）

回归总结

回归定义：当因变量的值是两个离散值时，我们称这是一个二分类模型。最基础二分类模型就是logistic 回归。

回归方程：

概率解释：

机会比率： 度量了当一组自变量中只有一个自变量增加了一个单位时对机会比的影响。

统计模型：这里只是统计意义上的logistic回归。它在更深入的机器学习领域有着更广泛的应用。

机会比率和机会比是非常重要的两个概念，需要好好理解消化。

在统计学上，我们特别强调可解释性。一个模型训练出来了，怎么来解释呢很重要，要能够阐述出来。

注意：在这个地方，我们并没有讲述logistic回归的具体算法，以及该如何评估该模型。