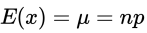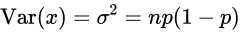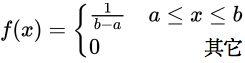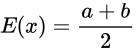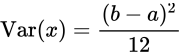概率

随机试验，计数法则(P91)

概率介绍

  • 概率
    • (probability)数值度量
      • 描述一个事件发生可能性的大小
    • 总是介于0到1之间
  • 随机试验
    • 试验结果是完全确定的
    • 出现哪种结果是偶然性的
    • 比如抛硬币
  • 样本空间
    • 所有可能的实验结果的集合
    • 比如{正，反}
  • 样本点
    • 一个试验的结果
    • 它是样本空间的一个元素
    • 比如{正}

多步骤试验计数法则

  • 多步骤试验（是为了计算样本空间的大小）
    • 考虑抛两枚硬币的试验，请问会出现多少种可能的试验结果？
    • 实验步骤：第一步抛掷第一枚硬币，第二步抛掷第二枚硬币
  • 树形图(可视化)
    • 列出每一步骤的试验结果，最后进行组合
  • 多步骤试验计数法则
    • 如果一个试验可以分为连续的k个步骤
    • 在第一步有n1种可能的结果
    • 在第二步有n2种可能的结果，以此类推
    • 那么所有的试验结果的个数为(n1)*(n2)….(nk)

多步骤实验举例，下图为抛两次硬币的实验可能结果：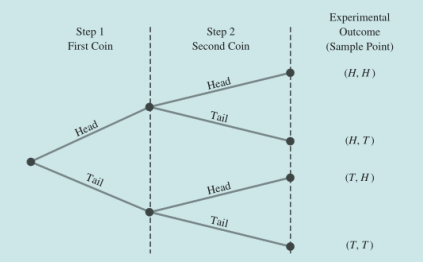
image.png

组合计数法则

  • 概念
    • 从N项中任取n项的组合数
      • 关键点：不考虑顺序
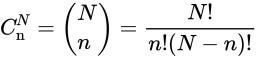
  • 公式 组合.png
  • 高中数学案例
    • 一个袋子当中装有5个不同编号的球，从中取出任意2个球，共有多少种不同的取法呢？
    • 首先这是一个试验，目的是计算样本空间的大小，计算总共有多少个样本点，即总共多少种试验结果
    • 应用组合计算公式，结果为10

排列计数法则

  • 概念
    • 从N个物体的集合中选取n个物品
      • 关键点：考虑顺序
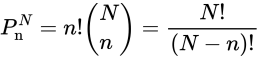
  • 公式 排列.png
  • 注意
    • n个物体考虑排序的选取有n阶乘种不同的方式
    • 排列的试验结果总是大于组合的试验结果
  • 高中数学案例
    • 同上
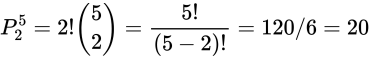
    • 排列举例.png

这里，C表示组合，不考虑顺序，P表示排列，要考虑顺序，排列与组合的计算公式是有必要记住的。

事件及其概率(P97)

  • 事件
    • 事件是样本点的一个集合
    • 假设该集合中共有n个样本点
    • 则n个样本点中的任意一种试验结果出现，我们就称该事件发生
  • 事件的概率
    • 事件的概率等于事件中所有样本点的概率之和

概率的基本性质(P99)

事件的补

  • 概念
    • 给定一个事件A，事件A的补是指所有不属于事件A的样本点组成的事件
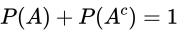
  • 公式 补集.png
  • 注意
    • 前提条件是在某一个样本空间内
      • 事件A在该样本空间内
      • 事件A的补也在该样本空间内
      • 它们的并集构成了整个的样本空间

事件的补，文氏图如下：
image.png

加法公式

  • 概念
    • 对于两个事件A和B
    • 我们希望知道事件A或事件B或两者都发生的概率时
    • 我们使用加法公式
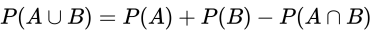
  • 公式 加法公式.png

我们来看一下具体的情况：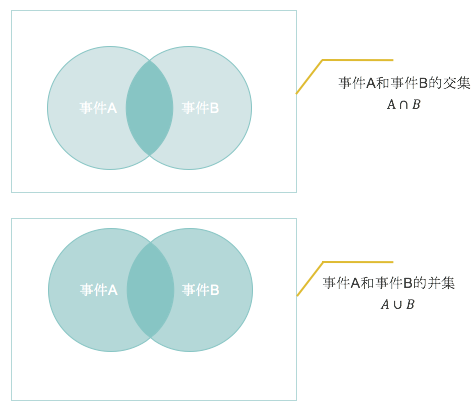
image.png
因为交集被计算了两次，因此我们计算并的概率时需要特别减去这个部分。

互斥事件

  • 概念
    • 如果两个事件没有公共的样本点，则称这两个事件互斥
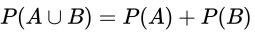
  • 互斥事件的加法公式 互斥事件的加法公式.png

互斥事件的文氏图如下：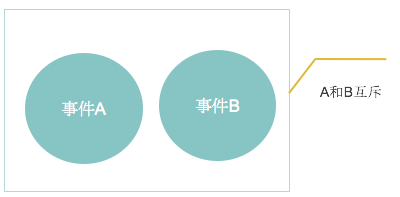
image.png

条件概率(P102)

  • 概念
    • 某个事件发生的可能性经常会受到另一个相关事件发生与否的影响
    • 假设事件A发生的概率为P(A)，且A事件的发生依赖于事件B的发生
    • 那么事件A发生的可能性叫做条件概率，记为P(A|B)
  • 公式
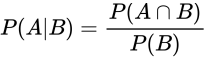
    • 条件概率.png
    • 联合概率 / 边际概率
  • 联合概率
    • 两个事件交的概率
    • 联合概率表
  • 边际概率
    • 是指联合概率表边缘的概率
      • 即某个事件的边缘概率
    • 边际概率总可以由联合概率表中的联合概率按行或按列求和得到
  • 独立事件
    • 概念
      • 假设事件A的概率受到事件B的影响，则它们是相依事件，不是独立事件
      • 如果P(A|M) = P(A) , 则称事件A与事件M是独立事件
    • 性质
      • 如果P(A|B) = P(A) , P(B|A) = P(B)
      • 则两个事件A和B是相互独立的
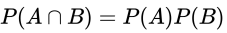
    • 独立事件的乘法公式 独立事件的乘法公式.png
  • 乘法公式
    • 概念
      • 用来计算两个相交事件的概率
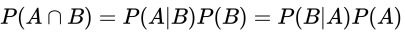
    • 通用公式 乘法公式.png
  • 互斥与独立
    • 这是两个不同的概念
    • 两个概率不为0的事件不可能既是互斥事件又是独立事件
    • 如果两个互斥事件之一已经发生，那么另一事件不会发生，因此这两个事件不是独立事件
    • 最重要的一点
      • 互斥事件A和B是在同一个样本空间内
      • 而独立事件A和B则是分属不同的样本空间

**

我们看一个具体的案例，考虑职员的升值与否与性别的关系：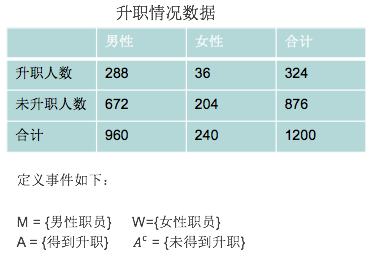
image.png
进一步计算出联合概率表如下所示：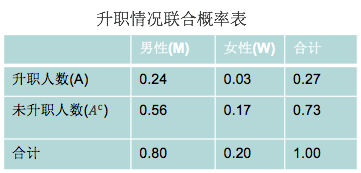
image.png
计算一下某位职员是男性的前提下升值的概率如下：
P(A|M) = P(A∩M) / P(M) = 0.24 / 0.80 = 0.3
同样计算一下是女性的前提下升值的概率：
P(A|W) = P(A∩W) / P(W) = 0.03 / 0.20 = 0.15 因此得出结论，性别对于升职与否是有影响的
我们可以看到，条件概率本质上就是联合概率/边际概率；而乘法公式不过是条件概率的变形罢了；

贝叶斯定理(P106)

  • 先验概率
    • 在获得新的信息之后对概率进行修正是重要的概率分析手段
    • 通常在开始分析前，总是对所关心的特定事件估计一个初始或先验概率
  • 后验概率
    • 然后从样本，专项报告或产品检验中获取了有关该事件的新信息
    • 就能根据这些新增的信息计算修正概率，更新先验概率值得到后验概率
  • 贝叶斯
    • 贝叶斯定理停供了这种概率计算的一种方法
  • 修正步骤
    • 先验概率—->新信息—->应用贝叶斯定理—->后验概率
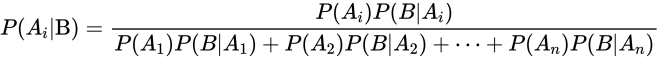
  • 公式 贝叶斯公式.png
  • 应用
    • 通常应用于如下情况
    • 即我们希望计算后验概率的那些事件是互斥的
    • 且它们的并集构成了整个样本空间

来看一个具体的案例：
假设某制造企业从两个不同的供应商处采购零件。令A1表示事件”零件来自于供应商1”，A2表示事件”零件来自于供应商2”。目前该企业有65%的零件采购自供应商1，其余35%采购自供应商2. 那么随机选取一个零件，因此可以设定先验概率P(A1)=0.65 和 P(A2)=0.35。同时两个供应商零件质量的历史数据如下所示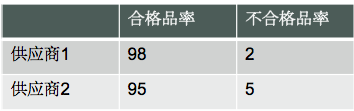：image.png
令G表示事件“零件合格”，B表示事件“零件不合格”。则可以得出如下的条件概率：
P(G | A1) = 0.98; P(B | A1) = 0.02; P(G | A2) = 0.95; P(B | A2) = 0.05;
我们想知道，在已知一个零件不合格的情况，来自供应商1的概率有多大？即求解P(A1 | B)
我们看一下这个树形图：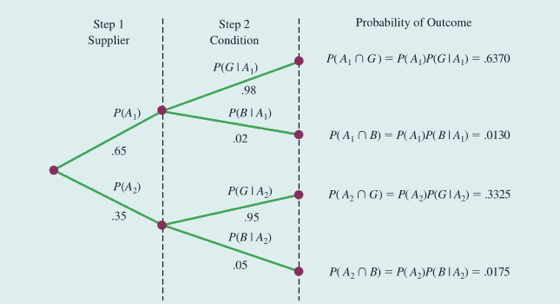
image.png
概率与随机变量分布 - 图19

我们可以看到开始随机选取的零件有0.65（先验概率）的概率来自于供应商1，
但是在给定零件不合格的信息以后，这个零件来自于供应商1的概率下降到0.4262（后验概率）。
要么来自供应商1，要么来自供应商2，这两个事件是互斥的，且共同构成了整个样本空间。

离散概率分布

随机变量(P116)

  • 定义
    • 对试验结果的数值描述
      • 比如抛硬币掷骰子
  • 解释
    • 随机变量将每一个可能出现的实验结果赋予一个数值
    • 随机变量的值取决于试验结果
  • 分类
    • 离散型随机变量
      • 可以取有限多个值或无限可数多个值
        • 比如性别，比如地球上的国家数
        • 比如自然数（无限但可数）
    • 连续性随机变量
      • 可以取某一个区间或多个区间内任意值的随机变量

离散型概率分布(P118)

  • 概率分布
    • 描述随机变量取不同值的概率
    • 对于离散型随机变量，会给出随机变量取每种值的概率，记作f(x)
  • 表达形式
    • 表格形式
    • 特定的数学函数
  • 古典法(P94)
    • 解释
      • 若各种实验结果是等概率发生的，适合采用古典法进行概率分配
      • 如果某一个试验有n个可能的试验结果，则为每个试验结果分配的概率均为1/n
    • 当各种试验结果对应的随机变量等概率时，适合采用古典法为随机变量的值分配概率
  • 相对频数法(P95)
    • 依据历史数据，采用相对频数法建立离散型概率分布得到所谓的经验离散分布
  • 离散型概率函数的基本条件
    • f(x) >= 0
    • ∑f(x) = 1
  • 离散型均匀概率函数
    • f(x) = 1/n
    • 其中n代表随机变量可能取值的个数

均匀概率分布举例：下图为抛掷一枚筛子朝上一面的概率分布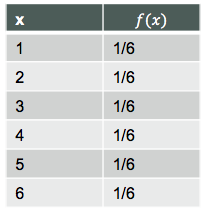
image.png
非均匀概率分布举例：下图为汽车日销量的概率分布（汽车公司过去300天的营业时间中，有54天汽车日销量为0，117天为1辆，72天为2辆，42天为3辆，12天为4辆，3天为5辆，可得54/300=0.18，即f(0) = 0.18，依次计算）
image.png
在实际应用中，古典法是不怎么常用的，用的最多的还是相对频数法。

数学期望与方差(P120)

  • 数学期望
    • 概念
      • 随机变量的数学期望或均值是对随机变量中心位置的一种度量
    • 离散型随机变量的数学期望
      • E(x) = u = ∑xf(x)
      • 想想离散型变量性别 男和女 怎么加起来求平均
  • 方差
    • 概念
      • 用来描述随机变量取值的变异性
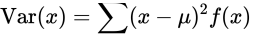
    • 离散型随机变量的方差 离散型随机变量的方差.png

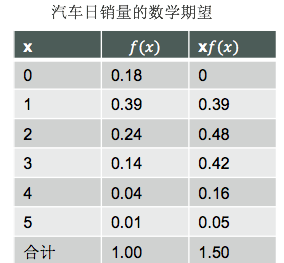
image.png
我们需要注意的就是：数学期望是有着实际意义的，而不仅仅就是一个数字，在这里，数学期望值等于1.5表达的是可以预期汽车公司平均日销量汽车1.5辆。如果一个月营业30天，可以预计汽车的平均销量为45辆。

二项概率分布(P128)

  • 二项试验的性质
    • 试验由一系列相同的n个试验组成
    • 每次试验有两种可能的结果，我们把其中一个称为成功，另一个称为失败
    • 每次试验成功的概率时相同的，用p来表示，失败的概率也是相同的，用1-p表示
    • 试验是相互独立的
  • 概念
    • 在二项试验中，我们感兴趣的是在n次实验中成功出现的次数。如果令x代表n次实验中成功的次数，则x的可能值为0，1，2.。。。n。由于随机变量取值的个数是有限的，所以x是一个离散型随机变量。与这一随机变量相对应的概率分布称为二项概率分布
  • 典型案例
    • 计算抛5次硬币中3次出现正面的概率
    • 强假设
    • 马丁服装店的问题
  • 类别公式
    • n次试验中恰有x次成功的试验结果的数目
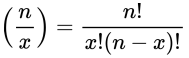
    • 二项分布类别.png
  • 二项概率计算
    • 我们想要确定n次试验中x次成功的概率，还必须知道其中每一个试验结果发生的概率
    • 由于二项试验的各个试验是相互独立的
      • 这一点非常重要
    • 我们只需要简单地将各个试验结果发生的概率相乘即可
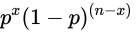
      • 应用乘法公式 二项分布概率.png
    • 在n次试验中有x次成功的特定试验结果的概率
      • 注意：一个是数目即类别，一个是每个类别的概率
      • 每个类别的概率都是相等的，总概率就是f + f + f…
      • 所以在概率函数那个地方可以看到公式为 数目 * f
  • 二项概率函数
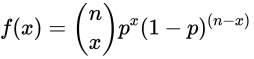
    • 二项分布概率函数.png
    • 解释
      • x代表成功的次数
      • p代表一次试验中成功的概率
      • n代表试验的次数
      • f(x)代表n次试验中有x次成功的概率
  • 二项分布的数学期望和方差
    • 二项分布期望.png
    • 二项分布方差.png

具体案例：
马丁服装店有3名顾客前来购买衣服，根据过去的经验，每名客人购买衣服的概率是0.3。那么，在3名顾客中有2名顾客购买服装的概率是多少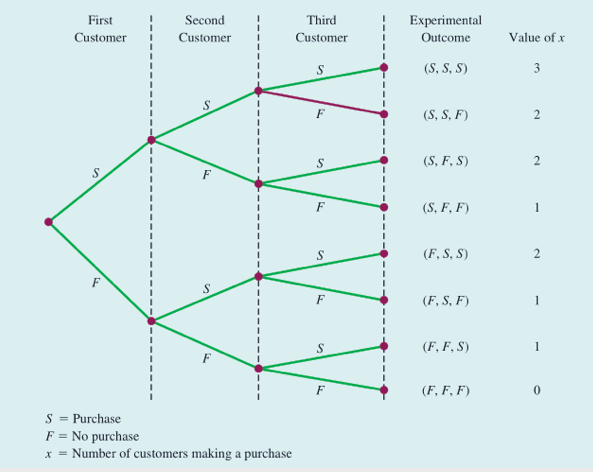？image.png
3名顾客中有2名顾客进行购买的概率如下：
pp(1-p)=0.3 ∗ 0.3 ∗ (1-0.3) = 0.063
那总共有多少种情况呢？即（S,S,F）(S,F,S) (F,S,S) 共三种情况。
0.063 3 = 0.189 即在3名顾客中有2名顾客购买服装的概率为0.189。
期望的计算为 0.3 n，意味着假设下个月有1000名顾客来光顾，那么实际购物的顾客人数期望值为300人。

毫无疑问，这个地方的计算是相对简单的，只是想说明一点，在二项概率函数的组成部分中，一部分表示概率，一部分表示组合的个数。

泊松概率分布(P134)

  • 概念
    • 主要用于估计某事件在特定时间段或空间中发生的次数
  • 性质
    • 任意两个长度相等的区间上，事件发生的概率是相同的
      • 概率相同
    • 事件在任一区间上是否发生与事件在其他区间上是否发生是独立的
      • 事件的独立性
    • 它的数学期望和方差相等
  • 泊松概率函数
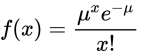
    • 泊松概率函数.png
    • 解释
      • f(x)代表事件在一个区间上发生x次的概率
      • u代表事件在一个区间上发生次数的数学期望
  • 案例
    • 时间上
      • 工作日早上7点到7点15之间到达停车场的汽车数量
      • 每辆车是否到达停车场，彼此之间是相互独立的
    • 空间上
      • 高速公路出发点至1000米内发生车祸的数量

具体案例：
我们感兴趣的是工作日早上15分钟内到达停车场的汽车数量：假设任意两个长度相等的事件内有一辆汽车到达的概率是相同的；假设任一时间段上是否有汽车到达与其他时间段是否有汽车到达相互独立；那么泊松概率在这里是适用的，并且根据历史数据显示，15分钟的时间段上到达车辆数目的平均值为10：
概率与随机变量分布 - 图31

如果管理员想知道15分钟内恰有5辆车到达的概率：
概率与随机变量分布 - 图32

泊松概率分布的一个重要性质是它的数学期望和方差相等，从而15分钟内到达车辆数的方差为 10。

假设需要计算3分钟内有1辆汽车到达的概率，又该如何计算呢？
由15分钟内到达车辆数的期望值为10可知，1分钟内到达的车辆数的期望值为10/15=2/3，于是3分钟内到达的车辆数的期望值为3*2/3=2。3分钟内有1辆汽车到达的概率如下：
概率与随机变量分布 - 图33

超几何分布(P137)

超几何分布与二项分布联系密切。这两种概率分布主要有两处不同：在超几何概率分布中，各次试验不是独立的，并且各次试验中成功的概率也不等。

举个简单的例子：不放回抽样概率的计算就属于超几何分布。具体可参考书本。

连续概率分布

随机变量

  • 连续型随机变量
    • 可以取某一个区间或多个区间内任意值的随机变量

区别

  • 离散型随机变量
    • 概率函数
      • 记为f(x)
    • 直接给出取某个特定值的概率
  • 连续型随机变量
    • 概率密度函数
      • 也记为f(x)
    • 取某个特定值的概率值为0是没有意义的
    • 讨论某一区间上的取值概率
      • 即给定区间上曲线f(x)下的面积
    • 函数性质
      • 曲线f(x)下方的面积为1，不管是什么分布
      • 对于所有的x值，都有f(x) >= 0

均匀概率分布(P145)

  • 概念
    • 任意一个单位区间内，它的概率值都是相同的
  • 概率密度函数
    • 均匀概率密度函数.png
  • 期望
    • 均匀概率期望.png
  • 方差
    • 均匀概率方差.png

均匀概率分布举例：下图为某一个飞机航班到达目的地所需的时间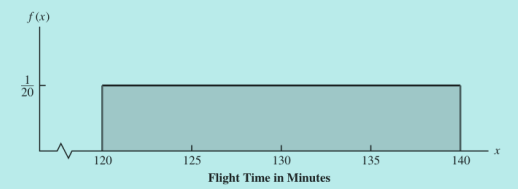
image.png
均匀概率分布中的计算是最为简单的了：直接求矩形面积就行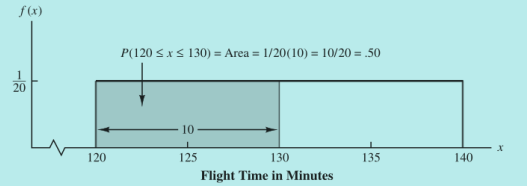
image.png

正态概率分布(高斯分布)(P148)

正态概率分布

  • 概念
    • 是描述连续型随机变量的最重要的一种概率分布
  • 概率密度函数
    • 概率与随机变量分布 - 图39
    • 解释
      • 平均数
      • 标准差
      • π=3.14159
      • e=2.71828
  • 性质
    • 正态分布簇中的每个分布因为均值和标准差这两个参数的不同而不同
    • 正态曲线的最高点在均值处达到，均值还是分布的中位数和众数
    • 分布的均值可以是任意值：负数，零，正数
    • 正态分布是对称的
      • 钟形，左右完全对称
    • 标准差决定曲线的宽度和平坦程度
      • 标准差越大则曲线越宽越平坦，表明数据更大的异动性
    • 正态随机变量的概率由正态曲线下的面积给出

正态分布公式及示意图如下：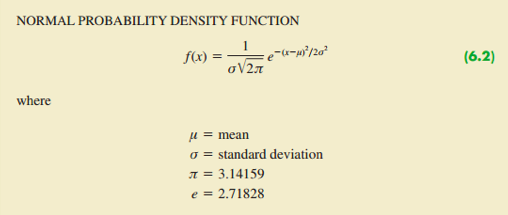
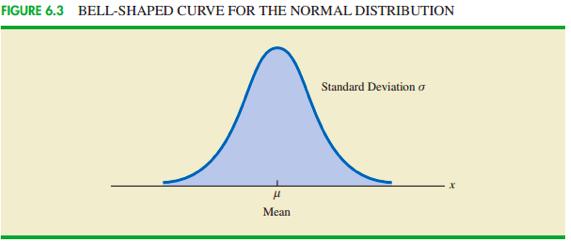
image.png
image.png
正态分布的第三条性质举例：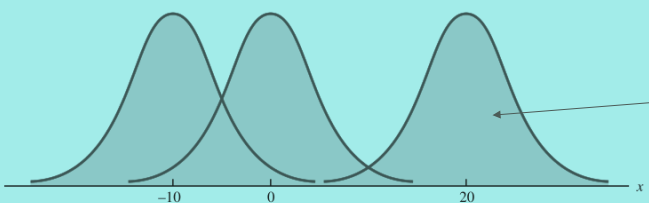
image.png
根据正态分布的第五条性质举例：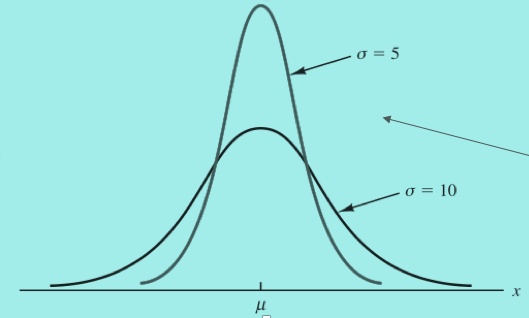
image.png

标准正态概率分布

  • 概念
    • 如果一个随机变量服从均值为0且标准差为1的正态分布，则称该随机变量服从标准正态分布
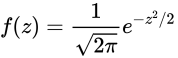
  • 标准正态概率密度函数 标准正态分布概率密度函数.png
  • 概率表
    • 对于标准正态分布，正态曲线下的面积已计算出来并且被编制成了表
    • 概率表中通常是没有z为负数时的概率的，因为是对称的，可以计算出来
    • 概率表对应的是z值小于或等于一给定值的概率
    • z等于0时 显示概率值为0.5 面积1的一半嘛
  • 三种类型概率
    • 标准正态随机变量z小于或等于一给定值的概率
    • z在两个给定值之间的概率
    • z大于或等于一给定值的概率
  • 正态分布标准化
    • 概念
      • 任何正态分布的随机变量我们都可以通过标准化转换
      • 将其概率求解转换为标准正态分布
      • 然后利用概率表进行求解
    • 公式
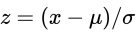
      • 标准化.png
      • 减去均值 / 标准差
      • 转换之后新的随机变量均值为0标准差为1
    • 实践
      • 想象一下为什么需要标准化，其实是为了更方便的计算概率
      • 两个方向的应用
        • 正向
          • 原数值 —-> z —-> 概率
        • 反向
          • 概率—-> z —-> 原数值

标准正态图形示例：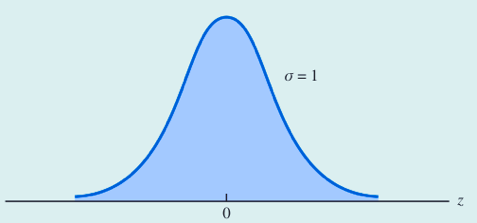
image.png
三种求解z值的情况图形化示例：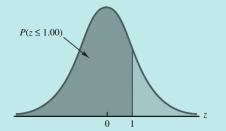
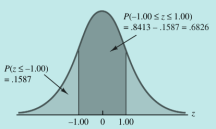
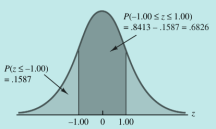
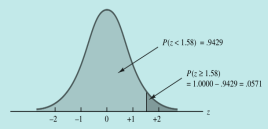
image.pngimage.png
image.png
image.pngimage.png
具体案例：
Grwar轮胎公司估计出开发出的新轮胎可行驶里程的平均数为36500，标准差为5000，收集的数据符合正态分布。预估一下可行驶里程超过40000的概率是多少？（属于常规情况：根据z值求概率，画出对应图形更加形象化）
解：
z = (40000 – 36500) / 5000 = 0.70
查表z = 0.70左边曲线面积为0.758
z大于0.70的概率为 1 – 0.758 = 0.242
即大约24.2%的轮胎行驶里程超过40000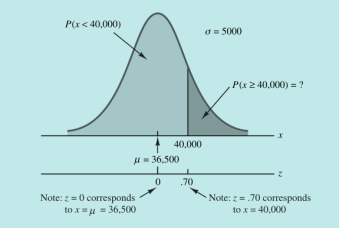
image.png
如果质量担保里程不达标， Grwar公司将会提供召回换胎服务，公司希望召回的比例不超过10%，那么质量担保的里程应该是多少？（属于是反向求解的情况：根据概率求解z值）
解：
左边曲线面积为0.1
查看概率表，得知z = -1.28
z = (x-μ)/σ = -1.28
x = μ – 1.28σ = 36500-1.28 * 5000 = 30100
即若设定质量保证为30100英里，则大约有10%的轮胎符合质量保证条件的要求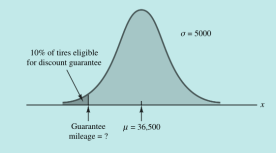image.png
注意这个地方，标准正态分布在质量担保方面的应用，它有着实际的应用意义。

指数概率分布(P155)

  • 概率
    • 对于诸如到达一家洗车房的两辆汽车的时间间隔、装载一辆货车所需的时间、公路上两起重大事故之间的距离等随机变量，可以用指数概率分布来描述
    • 描述的是一个间隔
    • 时间的间隔 或空间的间隔(距离)
    • 装载一辆货车所需的时间其实也是求间隔，即装第一件物品和装最后一件物品的时间间隔
  • 概率密度函数
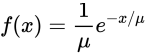
    • 指数概率密度函数.png
    • u代表期望值或均值
  • 性质
    • 指数分布的均值和标准差相等
  • 累积概率
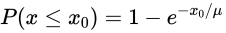
    • 指数分布累积概率.png
    • 最终计算概率是用的这个公式
  • 对比泊松分布
    • 泊松分布
      • 离散型的，给出的是取特定次数时的概率
      • 即每一区间中事件发生的次数
      • 比如10分钟内到达小区门口的人数
    • 指数分布
      • 连续型的，给出的是某一区间内的概率
      • 即事件发生的时间间隔长度
      • 比如货车在6-18分钟内装完货的概率
    • 存在一定的关联性，只不过刻画的对象不同
    • 一个刻画的是单个值，一个刻画的是某个区间上

指数分布图形示例：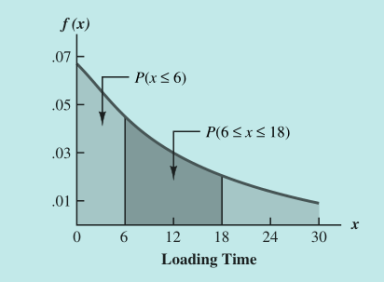
image.png
注意对上面累计函数的求导，结果就是我们的概率密度函数；是属于复合函数求导的过程。

具体案例：
假定在一小时当中到达某一洗车店的汽车数可以用泊松分布描述，其均值为每小时10辆。泊松概率函数给出了每小时有x辆汽车到达的概率：
概率与随机变量分布 - 图57
由于车辆到达的平均数是每小时10辆，则两车到达的时间间隔的均值为：
1小时/10辆车=0.1小时/辆
于是，描述两车到达的时间间隔的对应分布是指数分布，其均值为0.1小时/辆，从而指数概率密度函数为：

概率与随机变量分布 - 图58