成年人收入水平预测 --- 金融

项目的目的是根据一些特征，包括连续的，分类的，判断客户的年收入是大于50k，还是小于等于50k。数据集中每个数据列的含义如下所示：

• target: >50K, <=50K.
• age: continuous.
• workclass: Private, Self-emp-not-inc, Self-emp-inc, Federal-gov, Local-gov, State-gov, Without-pay, Never-worked.
• fnlwgt: continuous.
• education: Bachelors, Some-college, 11th, HS-grad, Prof-school, Assoc-acdm, Assoc-voc, 9th, 7th-8th, 12th, Masters, 1st-4th, 10th, Doctorate, 5th-6th, Preschool.
• education-num: continuous.
• marital-status: Married-civ-spouse, Divorced, Never-married, Separated, Widowed, Married-spouse-absent, Married-AF-spouse.
• occupation: Tech-support, Craft-repair, Other-service, Sales, Exec-managerial, Prof-specialty, Handlers-cleaners, Machine-op-inspct, Adm-clerical, Farming-fishing, Transport-moving, Priv-house-serv, Protective-serv, Armed-Forces.
• relationship: Wife, Own-child, Husband, Not-in-family, Other-relative, Unmarried.
• race: White, Asian-Pac-Islander, Amer-Indian-Eskimo, Other, Black.
• sex: Female, Male.
• capital-gain: continuous.
• capital-loss: continuous.
• hours-per-week: continuous.
• native-country: United-States, Cambodia, England, Puerto-Rico, Canada, Germany, Outlying-US(Guam-USVI-etc), India, Japan, Greece, South, China, Cuba, Iran, Honduras, Philippines, Italy, Poland, Jamaica, Vietnam, Mexico, Portugal, Ireland, France, Dominican-Republic, Laos, Ecuador, Taiwan, Haiti, Columbia, Hungary, Guatemala, Nicaragua, Scotland, Thailand, Yugoslavia, El-Salvador, Trinadad&Tobago, Peru, Hong, Holand-Netherlands.

探索数据

import numpy as np 
import pandas as pd 
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline

下面我们先看一下数据集的轮廓：

df = pd.read_csv('adult.csv')
df.head()

执行

特别关注一下我们的目标特征列：

df['income'].unique()               # array(['<=50K', '>50K'], dtype=object)

由输出可以看到，只有两个不同的值，是字符串类型的，我们将之替换为0，1数值类型。

df['income'] = df['income'].apply(lambda s: s.strip())
# 注意：可以通过这种方式进行列中数据的替换
df.loc[df['income'] == '<=50K', 'target'] = 0
df.loc[df['income'] == '>50K', 'target'] = 1
df.drop(columns='income', inplace=True)
df.head()

执行

重点观察target这一列的数据发生的变化。

df.shape                     # (48842, 15)

共有48842行的数据，还是蛮多的。下面我们在看一下样本类别0与类别1之间的比例：

df['target'].value_counts()

执行

0.0    37155
1.0    11687
Name: target, dtype: int64

可以看到，类别0与类别1的样本数量比例大约为3.5:1，不算是样本不均衡，还算正常。

预处理

我们需要谨记的一个原则是：一个项目准确率的上限不是取决于模型，而是取决于准备的特征和数据。特征和数据准备的越好，模型效果就越好，相反，模型带来的收益都是比较小的，甚至有时候模型的准确率就上不去了。数据和特征决定了算法的准确性的上限，而模型只是无限的逼近于这个上限。

from sklearn.model_selection import StratifiedKFold
# 所有列，共两类，一类连续，一类离散
cat_columns = ['workclass', 'education', 'marital-status', 'occupation', 'relationship', 'race', 
               'gender','native-country']
num_columns = ['age','fnlwgt','educational-num','capital-gain', 'capital-loss', 'hours-per-week']
target_column = "target"

我们将数据集的15个列分为值为离散的列，值为连续的列，以及目标列。针对它们作不同的处理。

离散特征进行热编码

热编码有很多种方式：使用pd.get_dummies的好处就在于可以自动去除原有的列名，并且使得新增的列名有清晰明了的含义。

# 离散特征进行热编码 one-hot-encode 
encode_df = pd.get_dummies(df, columns=cat_columns)
# 删除掉目标列后，作为输入特征
df_x = encode_df.drop(columns=target_column)
df_y = encode_df[target_column]
df_y = df_y.values

在这里，df_y本来是Series类型，之所以转为array类型，是后面我们划分数据集的时候，需要用到。

连续特征标准化

为什么需要进行连续特征标准化呢？梯度下降算法需要将连续特征进行标准化处理。详细来说：因为不同特征的度量尺度相差太大，比如这里的age和fnlwgt两列，导致我们针对每个自变量求解的梯度（即偏导数）在梯度下降中所占到的权重相差甚远，如果某个自变量的值过大，求解出的对应偏导数也大，对更新的参数影响大，相反如果值比较小，则影响小。我们希望每个自变量对参数的更新影响都不要太大，最好是比较接近的。

# 连续特征标准化
num_mean = df_x[num_columns].mean()
num_std = df_x[num_columns].std()
# 注意：这个地方多列同时进行z-score
num_normal = (df_x[num_columns] - num_mean) / num_std
num_normal.head()

执行

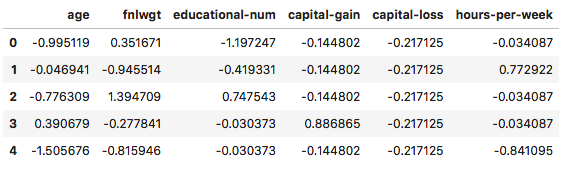
# 将原有的连续型数据列删除
df_x = df_x.drop(columns=num_columns)
# 横向拼接标准化数据
df_x = pd.concat([df_x, num_normal], axis=1)
# 注意：DataFrame也有values属性
df_x = df_x.values
df_x.shape                     # (48842, 108)

在这里，df_x本来是DataFrame类型，之所以转为二维数组ndarray的类型，也是后面划分数据集使用。可以看到，这个时候，我们的输入特征已经变成了108个特征。

训练/测试 数据集划分

划分数据集的时候，为什么不完全采用随机划分呢？假设这样几种情况，随机划分可能把都是0这个类别，或都是1这个类别全都划分到测试集中，再者，如果原始数据集中类别1与类别0的比例是3：1，但测试集样本中比例是10：1，那这样的测试数据集是完全没有意义的。因此，我们在划分数据集的时候要保证：划分后训练集和测试集中类别1和0的比例应该同原始数据集的比例是一样的，具体操作可通过分层划分来确保这一点。

# 指定划分为2个数据集
skf = StratifiedKFold(n_splits = 2)
# 注意：分层抽样需要转化为array的形式
for train_index, test_index in skf.split(df_x, df_y):
     trainx, testx = df_x[train_index], df_x[test_index]
     trainy, testy = df_y[train_index], df_y[test_index]

分别看一下训练集和测试集的size，如下所示：

trainx.shape                  # (24421, 108)
testx.shape                   # (24421, 108)

上面这种虽然保证了分层划分，但用一半的原始数据进行测试太浪费了。一般的数据集划分比例是70%用来训练，30%用来进行测试，我们指定划分数据集的比例，如下所示：

from sklearn.model_selection import StratifiedShuffleSplit
# 更为推荐这种划分样本的方法
sss = StratifiedShuffleSplit(n_splits=2, train_size=0.7)
# 注意：这里train_index和test_index给出的是数组的索引
for train_index, test_index in sss.split(df_x, df_y):
    trainx, testx = df_x[train_index], df_x[test_index]
    trainy, testy = df_y[train_index], df_y[test_index]

同样的，我们再次看一下训练集与测试集的样本size，如下所示：

trainx.shape                     # (34189, 108)
testx.shape                      # (14653, 108)

构建LR模型(梯度下降)

from sklearn.linear_model import SGDClassifier
# 指定loss参数值为’log‘，表明为logistic regression
lr = SGDClassifier(loss='log', max_iter=100)
# 训练模型
lr.fit(trainx, trainy)

执行

SGDClassifier(alpha=0.0001, average=False, class_weight=None,
              early_stopping=False, epsilon=0.1, eta0=0.0, fit_intercept=True,
              l1_ratio=0.15, learning_rate='optimal', loss='log', max_iter=100,
              n_iter_no_change=5, n_jobs=None, penalty='l2', power_t=0.5,
              random_state=None, shuffle=True, tol=0.001,
              validation_fraction=0.1, verbose=0, warm_start=False)

看一下模型预测的正确率有多少?

# 准确率accuracy计算
lr.score(testx, testy)       # 0.8524534225073364

在测试数据集上，获得了85%的正确率，还是很不错的。

from sklearn.metrics import roc_auc_score, roc_curve, precision_recall_curve, classification_report
# 获取测试集中每个样本为类别1的概率值，总共两列，第0列为类别0的概率，第1列为类别1的概率
pred = lr.predict_proba(testx)[:,1]
# 根据默认的阈值0.5，直接预测出测试集中每个样本对应的类别值
pred_labels = lr.predict(testx)
# t = pd.Series(pred) >= 0.5
# print(t.sum())                     # 3098
# t = pd.Series(pred_labels) == 1
# print(t.sum())                     # 3098

在上面的单元格中，最后面注释的四行代码是为了验证，它默认的阈值确实是0.5所作的。

# 前面我们说过，accuray准确率这种方式有它的弊端，我们来看一下precision、recall以及pr曲线
precision, recall, _ = precision_recall_curve(testy, pred)
# 绘制pr曲线，其中x轴对应recall，y轴对应precision
plt.plot(recall, precision)

执行

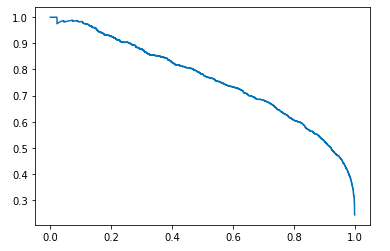
我们知道，一个阈值，对应着一个混淆矩阵，对应着一组precision、recall的值，因此函数precision_recall_curve返回的是三列数据，precision、recall、阈值，并且是一一对应的，下面是同样的道理。

# 即便precision-recall曲线，也有它的不完美之处，我们进一步绘制roc曲线
fpr, tpr, _ = roc_curve(testy, pred)
# roc曲线，其中x轴对应fpr，y轴对应tpr
plt.plot(fpr, tpr)

执行

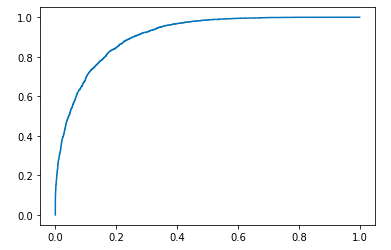
我们最常使用的指标应该是auc，即roc曲线下方的面积，我们来计算一下：

# 计算出roc曲线下方的面积，即auc
print(roc_auc_score(testy, pred))
# 打印阈值为0.5的情况下的分类报告
print(classification_report(testy, pred_labels))

执行

0.9078955677667694
              precision    recall  f1-score   support
         0.0       0.89      0.92      0.90     11147
         1.0       0.72      0.63      0.67      3506
    accuracy                           0.85     14653
   macro avg       0.80      0.78      0.79     14653
weighted avg       0.85      0.85      0.85     14653

可以看到，roc下方的面积约为91%，同时我们也能看到在测试数据集下不同类别的precision，recall，f1-score。

更多特征探索

def _combineFeatures(df,columns):
    combine_columns = []
    for i in range(len(columns) - 1):
        for j in range(i+1,len(columns)):
            temp_col = columns[i] + "_" + columns[j]
            combine_columns.append(temp_col)
            df[temp_col] = df[columns[i]].astype("str") + "_" + df[columns[j]].astype("str") 
    return df,combine_columns
# combine_df,combine_columns = _combineFeatures(df,cat_columns)
# 我们对分类特征进行横向的concat操作，即作特征工程
# 这里我们选取education与occupation、race与gender，当然也可以做三个或三个以上的特征concat操作
combine_df = df
combine_df['education_occupation'] = df['education'] + df['occupation']
combine_df['race_gender'] = df['race'] + ['gender']
cat_columns.extend(['education_occupation', 'race_gender'])
# 下面是同之前一样的操作流程
# 离散特征热编码 one-hot-encode
encode_df = pd.get_dummies(combine_df, columns=cat_columns)
# 分离输入特征与目标值
df_x = encode_df.drop(columns=target_column)
df_y = encode_df[target_column]
df_y = df_y.values
# 删除掉没有标准化的连续型特征
df_x = df_x.drop(columns=num_columns)
# concat标准化数据
df_x = pd.concat([df_x, num_normal], axis=1)
df_x = df_x.values
# 划分数据集
for train_index,test_index in sss.split(df_x,df_y):
    trainx,testx = df_x[train_index],df_x[test_index]
    trainy,testy = df_y[train_index],df_y[test_index]

继续使用SGDClassifier梯度下降构建LR模型，并进行训练：

lr = SGDClassifier(loss='log', max_iter=100, n_jobs=-1, alpha=0.01)
lr.fit(trainx, trainy)

执行

SGDClassifier(alpha=0.01, average=False, class_weight=None,
              early_stopping=False, epsilon=0.1, eta0=0.0, fit_intercept=True,
              l1_ratio=0.15, learning_rate='optimal', loss='log', max_iter=100,
              n_iter_no_change=5, n_jobs=-1, penalty='l2', power_t=0.5,
              random_state=None, shuffle=True, tol=0.001,
              validation_fraction=0.1, verbose=0, warm_start=False)

同样的，我们查看模型正确率，roc曲线下方的面积：

# 注意到模型的正确率下降了，之前约为85%
print(lr.score(testx, testy))                  # 

pred = lr.predict_proba(testx)[:,1]
pred_labels = lr.predict(testx)

# ROC AUC 注意到AUC的值降低了，之前约为91%
print(roc_auc_score(testy, pred))

# 分类报告
print(classification_report(testy, pred_labels))

执行

0.843786255374326
0.8976381132069485
              precision    recall  f1-score   support

         0.0       0.87      0.94      0.90     11147
         1.0       0.73      0.55      0.63      3506

    accuracy                           0.84     14653
   macro avg       0.80      0.74      0.76     14653
weighted avg       0.84      0.84      0.84     14653

这里，我们虽然是基于原有特征构建了三个新增特征，但模型效果不升反降，说明特征选取并不好。另一方面，也说明了靠模型效果提升获取的收益是有限的，还是应该回归到数据收集以及特征处理上。

构建LR模型(牛顿法)

下面是使用牛顿法的logistic regression，更建议通过这样的方式，同样可以用来预测和评估。

from sklearn.linear_model import LogisticRegression

lr = LogisticRegression(n_jobs=-1, max_iter=100, verbose=1, C=0.01, solver='newton-cg')

lr.fit(trainx, trainy)

执行

LogisticRegression(C=0.01, class_weight=None, dual=False, fit_intercept=True,
                   intercept_scaling=1, l1_ratio=None, max_iter=100,
                   multi_class='auto', n_jobs=-1, penalty='l2',
                   random_state=None, solver='newton-cg', tol=0.0001, verbose=1,
                   warm_start=False)

同样的，我们查看模型正确率，roc曲线下方的面积：

print(lr.score(testx, testy))

pred = lr.predict_proba(testx)[:, 1]
pred_labels = lr.predict(testx)

# ROC AUC
print(roc_auc_score(testy, pred))

# 分类报告
print(classification_report(testy, pred_labels))

执行

0.8468572988466526
0.9018542384197161
              precision    recall  f1-score   support

         0.0       0.87      0.93      0.90     11147
         1.0       0.73      0.57      0.64      3506

    accuracy                           0.85     14653
   macro avg       0.80      0.75      0.77     14653
weighted avg       0.84      0.85      0.84     14653

非线性模型展望

from sklearn.ensemble import GradientBoostingClassifier

rfc = GradientBoostingClassifier(max_depth=6)

# 运行时间大概在3~5分钟
rfc.fit(trainx, trainy)

执行

GradientBoostingClassifier(ccp_alpha=0.0, criterion='friedman_mse', init=None,
                           learning_rate=0.1, loss='deviance', max_depth=6,
                           max_features=None, max_leaf_nodes=None,
                           min_impurity_decrease=0.0, min_impurity_split=None,
                           min_samples_leaf=1, min_samples_split=2,
                           min_weight_fraction_leaf=0.0, n_estimators=100,
                           n_iter_no_change=None, presort='deprecated',
                           random_state=None, subsample=1.0, tol=0.0001,
                           validation_fraction=0.1, verbose=0,
                           warm_start=False)

同样的，我们查看模型正确率，roc曲线下方的面积：

# 就正确率accuracy而言，提高了2个百分点
print(rfc.score(testx, testy))

pred = rfc.predict_proba(testx)[:, 1]
pred_labels = rfc.predict(testx)

# ROC AUC 从结果可以看到，提高了大约2.5个百分点
print(roc_auc_score(testy, pred))

# 分类报告
print(classification_report(testy, pred_labels))

执行

0.8716303828567529
0.9256873771761706
              precision    recall  f1-score   support

         0.0       0.89      0.94      0.92     11147
         1.0       0.78      0.65      0.71      3506

    accuracy                           0.87     14653
   macro avg       0.84      0.79      0.81     14653
weighted avg       0.87      0.87      0.87     14653