单变量
数据类型
- 分类型变量
- 用标签或名称来识别项目的类型
- 比如:性别,国家,种类等
- 数量型变量
- 表示多少或大小的数值
- 比如年龄,身高,体重,重量等
大多数情况下,数量型数据都是连续的,不过在具体的情景下,也存在离散的数量型数据。(具体参考P31)
汇总分类型变量数据(P22)
- 表格法
- 频数分布
- 是一种数据的表格汇总方法
- 表示几个互不重叠组别中,每一组项目的个数(即频数)
- 相对频数分布
- 对每一组的项目所占的比例或百分比更感兴趣
- 一组的相对频数是属于该组别的项目个数占总数的比例
- 频数分布
- 图形法
- 条形图(又叫柱状图)
- 用来描绘已汇总的分类型数据的频数分布,相对频数分布
- 饼形图
- 是一种描述分类型数据的相对频数(百分数频数)分布的图形方法
- 条形图(又叫柱状图)
频数分布举例:下图是根据127次购买软饮料的样本数据统计出来的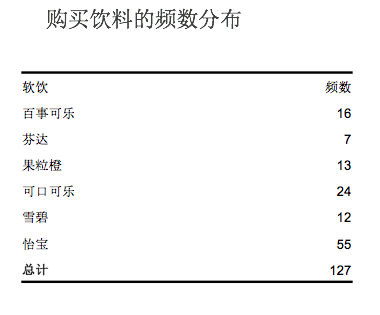
相对频数分布举例: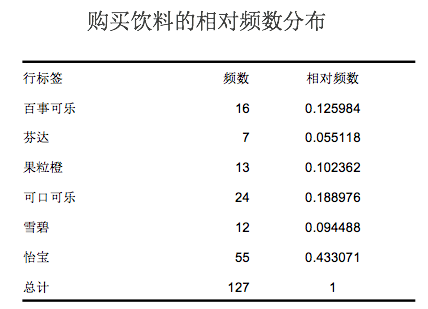
柱状图(也叫条形图)举例: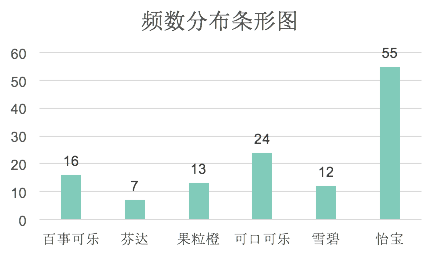
饼图举例: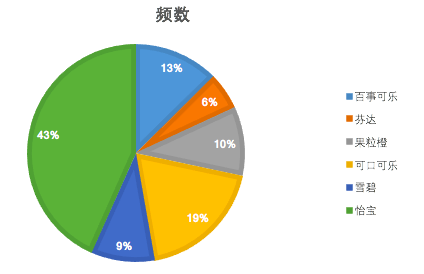
汇总数量型变量数据(P25)
频数分布
这应该是我们小学或初中就学习过的数学知识,应该还算是比较简单的。
- 确定组数
- 概念
- 总共要分成多少个组
- 组是通过对数据规定范围形成的,这个规定的范围作用于对数据进行分组
- 分组的目的是用足够多的组来显示数据的变异性
- 一般性原则
- 5-20组即可
- 注意
- 具体多少个组是和业务需求密切相关的
- 需要不断的尝试划分为7个组怎么样,划分为8个组怎么样。。。
- 比如你想要宽度为2的组宽,那应该划分成多少个组
- 概念
- 确定组宽
- 概念
- 每个组的宽度是多少
- 组宽和组数是互相依赖的
- 较大的组数意味着较小的组宽,反之亦然
- 一般性原则
- 每组的宽度相同
- 计算
- (数据最大值 - 数据最小值) / 组数
- 概念
- 确定组限
- 概念
- 每个组的上限下限是怎么确定的
- 比如左开右闭
- 选组组限必须使每一个数据值属于且仅属于一组
- 每个组的上限下限是怎么确定的
- 概念
数量型数据的频数分布举例: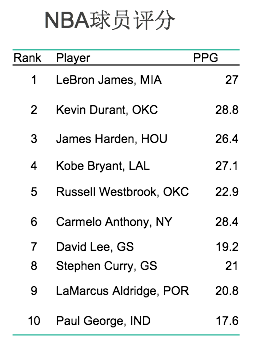
实践:
df = pd.read_csv('NBAPlayers.txt', sep='\t')h = df['height'].head(10)grouped = pd.cut(h, bins=5, right=True, include_lowest=False)grouped.value_counts().sort_index().plot.bar()
这里用了cut方法,进行切割分组,解释一下用到的参数,参数include_lowest值为True或False时,第一个区间左边界的值是不同的;参数right为True则左开右闭,为False则左闭右开
直方图
- 概念
- 常见的数量型数据的图形描述法
- 由先前已汇总的频数分布等数据进行绘制
- 变量标签放置在横轴上,频数放置在纵轴上
- 对比
- 条形图的类别之间都是分隔的,相互独立 即bar chart
- 但是直方图类别之间是没有分隔的,是连续的,代表数值变量
- 意义
- 直方图更重要的意义是表明一个变量的偏态分布
- 能够知道数据的分布趋势
数量型数据的直方图举例: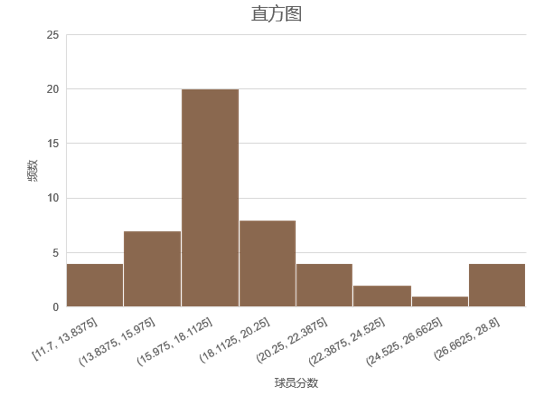
这里想额外补充一点:条形图和直方图本质上是同一事物,它们都是频数分布数据的图形表示。直方图是各纵条之间没有间隔的条形图。有些离散的数量型数据,各纵条之间有间隔是合适的。
实践:
# 使用matplotlib来绘图
import matplotlib.pyplot as plt
plt.hist(h, bins=3)
# 使用Pandas API来绘图
h.plot.hist(bins=3)
# 查看划分每个箱子(分组)的详情
pd.cut(h, bins=3).value_counts().sort_index()
前两个就是输出直方图了,共有3个分组,我们只看一下每个分组的情况是怎样的
(177.982, 184.0] 4
(184.0, 190.0] 1
(190.0, 196.0] 5
Name: height, dtype: int64
累积分布
- 累积频数分布
- 表明的是小于或者等于每一组上组限的数据项个数
- 每一组都有上限和下限,毫无疑问,上限是组范围的上边界
- 累积相对频数分布
- 表明数值小于或等于每一组上组限的数据项的比例
累计分布举例: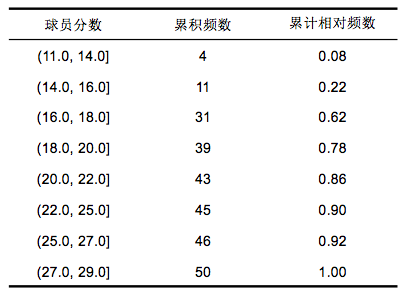
实践:
pandas中有cumsum函数可以用来求累积
s1 = pd.Series({'小于1万': 0.2, '大于1万小于3万': 0.7, '大于3万': 0.1})
s1.cumsum().values # array([0.2, 0.9, 1. ])
总结
- 条形图与直方图本质上是同一事物,他们都是频数分布数据的图形表示
- 开口组是指只有一个下组限或上组限的组(区间是开区间还是闭区间的问题)
- 对于数量型数据,适当的组限依赖于数据的精度水平(取几位小数的问题)
- 累积频数分布的最后一个数据项总等于观测值的总数
双变量
表格法(P33)
- 交叉分组表
- 概念
- 是一种汇总两个变量数据的方法
- 两个变量可以是分类的或是数量的
- 但是更常见的是一个为分类一个为数量
- 应用
- 左边栏和顶部边栏的标记确定了两个变量的组别
- 样本中的每个数据项都会落在交叉表的一个单元格里
- 表格解读
- 概念
交叉分组表举例: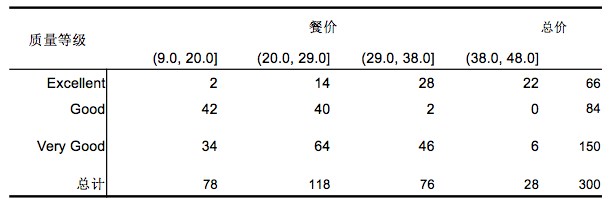
图形法(P37)
- 散点图
- 散点图是对两个数量变量间关系的图形表述
- 趋势图
- 趋势图是显示相关性程度的一条直线
- 注意趋势图是一条直线
- 猜测应该是拟合的线性回归直线
- 复合条形图
- 对于已经汇总的多个条形图同时显示的一种图形显示方法
- 解读
- 结构条形图
- 每一个长条被切割成不同颜色的矩形段,每一个段都表明一个频数百分比
- 解读
散点图与趋势图举例: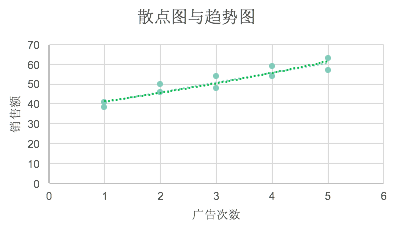
复合条形图举例: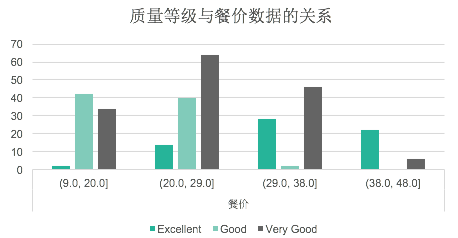
结构条形图举例: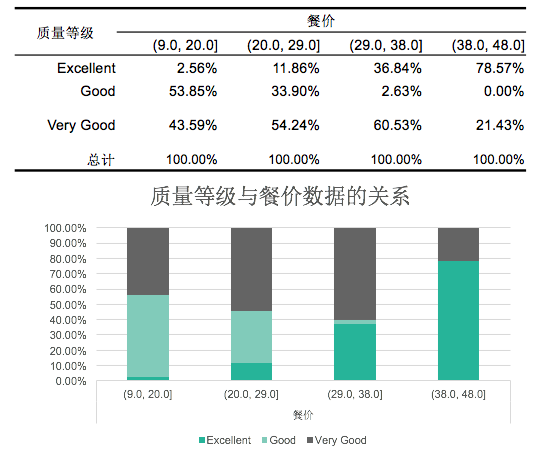
数值方法
位置的度量(P52)
- 平均数
- 加权平均数
- 每个数乘以权重的累加和 / 总的权重
- 几何平均数
- 中位数
- median
- 众数
- mode
- 四分位数
- Q1 = 25百分位数
- Q2 = 50百分位数
- 也等于中位数
- Q3 = 75百分位数
- 百分位数
- 定义
- 百分位数提供了数据如何散布在从最小值到最大值的区间上的信息
- 第p个百分位数是满足下列条件的一个数值
- 至少有p%的观测值小于或者等于该值
- 且至少有(100 - p)%的观测值大于或者等于该值
- 计算方式
- 把数据从小到大排序
- 计算指数 i = (p / 100) * n
- p是所求的百分位数,n是观测值的个数
- 若i不是整数,则向上取整。大于位置i的下一个整数表示第p百分位数
- 若i是整数,则第p百分位数是第i项和第i+1项数据的平均数
- 定义
经过上网查询资料,发现百分位数的计算并不仅仅是只有上面一种计算方式的,许多方法都可以用来计算样本数据的第p百分位数的位置。特别的,对于大型数据,所有方法都给出相近的数值。
变异程度的度量(P61)
- 极差
- 是一种最简单的变异程度的度量
- 极差 = 最大值 - 最小值
- 容易受到异常值影响,很少单独使用
- 四分位数间距
- interquartile range (IQR)
- IQR = Q3 - Q1
- 方差
- 概念
- 用所有数据对变异程度所做的一种度量
- 方差依赖于每个观察值与平均值之间的差异
- 拥有较大方差的变量显示其变异程度较大
- 公式
- 总体方差:
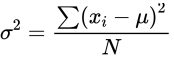
- 样本方差:
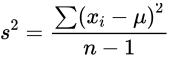
一般计算的都是样本方差,因为我们通常情况下很难取到全部数据
- 总体方差:
- 概念
- 标准差
- 概念
- 定位为方差的平方根
- 标准差和原始数据的单位度量相同
- 更容易与平均数等同样的度量单位数值比较
- 公式
- 样本标准差:
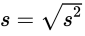
- 总体标准差:
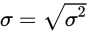
- 样本标准差:
- 概念
- 标准差系数
- 概念
- 标准差相对于平均数大小的描述统计量
- 公式
- ((标准差 / 平均数) * 100)%
- 概念
分布形态与标准化(P65)
- 分布形态
- 概念
- 前面的直方图对分布形态提供了一种很好的图形描述
- 分布形态的一种重要的数值度量称为偏度(skewness)
- 解读
- 数据总体左偏时,偏度是正数,平均数比中位数要大
- 数据总体右偏时,偏度是负数,平均数比中位数要小
- 当数据严重偏离时,中位数是位置的首选度量
- 举例
- 1000个员工,990个员工工资是1000,10个高管工资是100000
- 那么这个时候计算出来的平均工资毫无意义,反而中位数是有价值的
- 这个情况下平均工资肯定是大于中位数的,数据是左偏的情况
- 大部分的数据都分布在1000这个位置(新闻里老拿平均工资说事)
- 概念
- 标准化z-score
- 概念
- 对数据集中观测值相对位置的度量
- 帮助我们确定一个数值距平均数有多远
- 公式
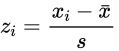
- 样本值减去平均数除以标准差
- 相对平均数的位置/度量单位:标准差
- 意义
- z-分数常被称为标准化数值
- 它能被解释为xi与平均数的距离是zi个标准差
- 两个不同数据集的观测值具有相同的z分数,就可以说明他们具有相同的相对位置(相对于平均数的位置,度量单位是标准差,比如1.5个标准差)
- 可以消除不同量纲单位带来的影响,比如同样度量身高,用不同的单位米和英尺
- 概念
分布形态举例: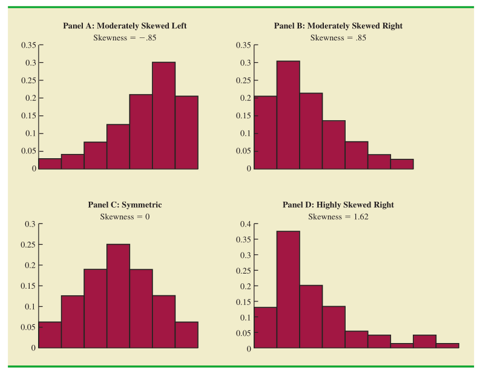
以上图中第一个子图(左上方位置)为例,是属于左偏的情况,为什么这么说呢?因为该图形的尾巴向左边延伸了一些,因此称之为左偏。考试成绩就是这种直方图的典型应用。因为没有成绩在100%以上,而大部分成绩又在70%以上,只有极少数的成绩很低。(图形的两边都称之为尾巴)
第二个子图(右上方位置)有一定程度的右偏,因为该图形的尾巴向右边延伸了一些,因此称之为右偏。像房屋价格的数据很可能就是这种直方图的例子,少数昂贵的住宅造成右尾偏斜。
第三个子图(左下方位置)是属于对称的,左尾和右尾的形状相同。像人的身高体重等数据得到的直方图。
第四个子图(右下方位置)是属于严重右偏的。在商务与经济应用中得到的数据,常常使直方图右偏。例如,房屋价格,工资,销售量等数据,常常导致直方图右偏。
切比雪夫定理与异常值检测(P67)
- 切比雪夫定理
- 概念
- 与平均数的距离在某个特定个数的标准差之内的数据值所占的比例
- 定理
- 与平均数的距离在z个标准差之内的数据值所占比例
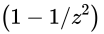
- 至少为1-z平方分之一,其中z是大于1的任意实数
- 经验应用
- 至少75%的数据值与平均数的距离在z=2个标准差之内
- 至少89%的数据值与平均数的距离在z=3个标准差之内
- 至少94%的数据值与平均数的距离在z=4个标准差之内
- 概念
- 异常值检测
- 概念
- 一个或者多个数值异常大或异常小的观测值,这样的极端值被称为异常值
- 异常值的原因:错误记录数值,一个错误的数据,反常的数据值
- 比如淘宝双十一当天的成交额属于反常的数据值,但不是异常值
- 计算方式
- IQR = Q3 - Q2
- 下限 = Q1 - 1.5 * IQR
- 上限 = Q3 + 1.5 * IQR
- 观测值大于上限或者小于下限就被归类为异常值
- 与图形对比
- 最大值应该是排除掉异常值之后数据集的最大值
- 即排除掉大于上限的值
- 即排除掉大于 (Q3 + 1.5 * IQR)
- 最小值是同理的
- 想一想落在线箱图外面的点,就属于是异常值
- 概念
线箱图举例: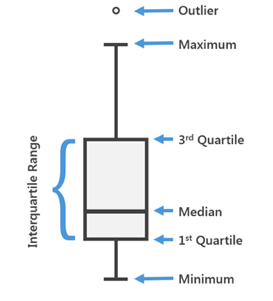
五数概括法和箱形图(P70)
- 五数
- 最大值
- 注意计算方式要排除掉异常值
- Q3 第三四分位数
- 中位数
- Q1 第一四分位数
- 最小值
- 注意计算方式要排除掉异常值
- 最大值
- 箱形图
- 概念
- 是基于五数概括法的数据图形汇总
- 关键是计算IQR(Q3 - Q1),箱体中代表的是中位数,Q1,Q3
- 异常值
- 超过Q1或者Q3的1.5倍IQR就被认为是异常值
- 概念
- 应用
- 可以作一个变量的箱型图
- 也可以作多个变量的箱型图
- 比如不同专业的薪资水平,每个专业的薪资数据集可以用一个箱型图表示
箱型图举例: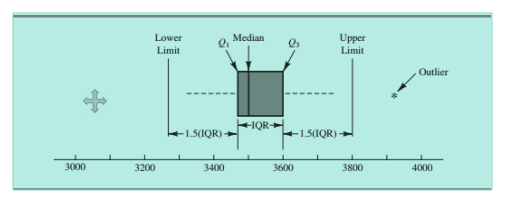
这里想补充一点:上图中的虚线,我们称之为触须线,通常来说Lower Limit(上限=Q1 - 1.5 IQR)和Upper Limit(下限=Q3 + 1.5 IQR)是不绘制出来的,触须线从箱体的边界一直画到上下限以内的原始数据的最大值和最小值处。这一点要特别注意。
单个专业薪资箱型图举例: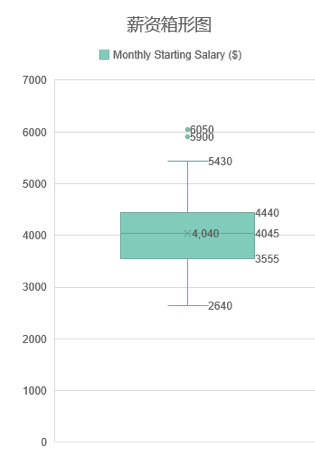
多个专业起始月薪箱型图举例: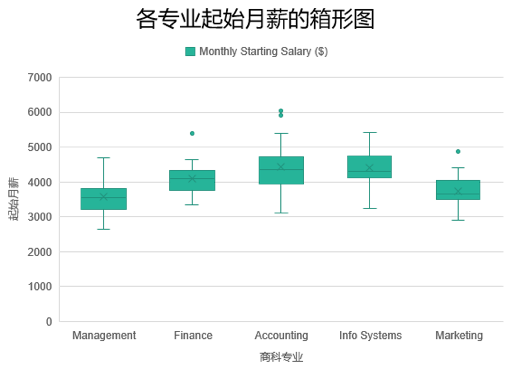
从上图这个图,我们能看出什么信息呢?
- 会计专业的薪资区间总体较高,管理和市场专业则比较低
- 会计专业存在起薪特别高的异常值,应该是有特别优秀的人才
- 根据中位数,会计,信息专业有着较高的起薪,金融次之,其它专业较低
两连续数值变量关系的度量(P73)
协方差
- 公式
- 样本协方差

- 总体协方差
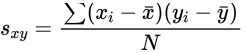
- 样本协方差
- 解释
- 一个大的正数表示强的正线性相关
- 一个大的负数表示强的负线性相关
- 缺点
- 虽然协方差表示有强的线性相关,但这个强度有多大,无法衡量
- 协方差依赖于x和y的计量单位
- 比如销售量y扩大了10倍,协方差也扩大了10倍
- 这就表明比之前的相关性要强么,并不能这么说,扩大无意义
相关系数(皮尔逊相关系数)
- 公式
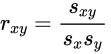
- 参数说明
- rxy是相关系数
- sxy是协方差
- sx是x的标准差
- sy是y的标准差
- 参数说明
- 解释
- 相关系数的值在-1 至 1之间
- 其绝对值越大,表明变量之间的相关性越大
- 正负号代表的是相关性的方向
- 很好的解决了协方差的两个弊端
- 注意
- 相关性系数提供的是两个变量之间关联性的度量
- 并不意味着他们之间存在因果关系
- 比如气温低,降雨量就大么

