离散
第一题 餐厅菜品
加拿大一座城市的商会对其大都会区域的 300 家餐厅进行评估。每家餐厅的菜品价格有 3 个等级,从 1 最便宜到 3 最贵;品质有 3 个等级,从 1 最差到 3 最好。下表是等级数据的列联表,有 42 家餐厅的菜品价格等级是 1,品质等级是 1;有 39 家餐厅的菜品价格等级是 2,品质等级是 1;以此类推。有 48 家餐厅的菜品价格等级和品质等级都是最高级别3。
| 品质(x) | 菜品价格(y) | 合计 | ||
|---|---|---|---|---|
| 1 | 2 | 3 | ||
| 1 | 42 | 39 | 3 | 84 |
| 2 | 33 | 63 | 54 | 150 |
| 3 | 3 | 15 | 48 | 66 |
| 合计 | 78 | 117 | 105 | 300 |
- 从加拿大这所城市随机选取一家餐馆,建立品质等级和菜品价格的二元概率分布。令x=品质等级,y=菜品价格。
- 计算品质等级 x 的数学期望和方差。
- 计算菜品价格 y 的数学期望和方差。
- Var(x+y)=1.6691,计算 x 和 y 的协方差。品质等级和菜品价格之间的关系如何?是你预期的那样吗?
- 计算品质等级和菜品价格的相关系数。二者关系的强弱程度如何?你认为在这所城市里找到物美价廉的餐馆是一件容易的事吗?为什么?
解答:
df = pd.DataFrame([[42, 39, 3], [33, 63, 54], [3, 15, 48]], index=[1,2,3], columns=[1,2,3])df['total'] = np.sum(df, axis=1)df.loc['total'] = np.sum(df)df
先构建一下我们的数据集: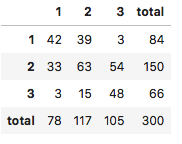
第一问
for col in df.columns:df.loc[col] = df.loc[col] / 300df
执行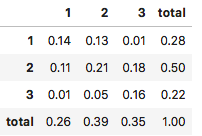
关于两个随机变量的概率分布称为是二元概率分布
第二问
x = [1, 2, 3]fx = [0.28, 0.5, 0.22]xe = 0for i in range(3):xe += x[i] * fx[i]xvar = 0for i in range(3):xvar += (x[i] - xe) * (x[i] - xe) * fx[i]print(xe) # 1.94print(xvar) # 0.4964
这说明这300家餐厅的菜品品质等级总体来说是处于中等水平的。
第三问
y = [1, 2, 3]fy = [0.26, 0.39, 0.35]ye = 0for i in range(3):ye += y[i] * fy[i]yvar = 0for i in range(3):yvar += (y[i] - ye) * (y[i] - ye) * fy[i]print(ye) # 2.09print(yvar) # 0.6019
这说明这300家餐厅的菜品价格水平总体来说是处于中等的。
第四问
猜测菜品的品质等级与菜品的价格之间应该有正的相关性
xy = (1.6691 - xvar - yvar) / 2print(xy) # 0.2854
结果说明菜品等级与菜品价格之间存在正相关。
注意:这个地方求解两个随机变量x和y的协方差计算公式(具体可参考课本P124),计算样本数据的协方差和计算两个随机变量之间的协方差完全是不同的计算公式,要区分开来,样本数据中x和y是一一对应的,而如果是两个随机变量x和y,则它们各自可能有不同的作用域。
第五问
p = xy / (np.sqrt(xvar) * np.sqrt(yvar))p # 0.5221
想想我们计算样本系数的公式,协方差/标准差之积
菜品等级和菜品价格间存在正的相关关系,不强也不弱,属于中等。我认为找到物美价廉的餐馆并不是一件容易的事,但是花费一些力气应该还是可以找到的,毕竟“一分价钱,一分货”,尽管如此,我们还是尽可能的选取性价比高的餐馆。
第二题 摩根大通资产管理
摩根大通资产管理公布了理财投资的信息。在过去 10 年里,S&P500 的期望收益率为 5.04%,标准差为19.45%。同一时期某核心债券的期望收益率为 5.78%,标准差为 2.13%(摩根大通资产管理,《市场指南》,2012年第1季 度)。公告报告了 S&P500 和核心债券的相关系数为-0.32。考虑一个资产投资组合,由 S&P500 指数基金和核心债券基金组成。
- 根据所给出的信息,求 S&P500 和核心债券的协方差。
- 建立一个资产投资组合,S&P500 指数基金投资和核心债券基金投资各占 50%。求资产组合的期望收益率和标准差。
- 建立一个资产投资组合,S&P500 指数基金投资占 20%,核心债券基金投资占 80%。求资产组合的期望收益率和标准差。
- 建立一个资产投资组合,S&P500 指数基金投资占 80%,核心债券基金投资占 20%。求资产组合的期望收益率和标准差。
- (2)、(3)和(4)中,哪个资产组合的预期收益率最高?哪个的标准差最小?哪个资产组合投资最优?
- (2)、(3)和(4)中,讨论这三种投资资产组合的优点和缺点。你偏好将所有资金都投资于 S&P500 指数、核心债券还是三种资产组合之一?为什么?
在计算之间,我们先看几个公式:
随机变量x和y的协方差:
随机变量x和y的相关系数:
随机变量x和y的线性组合的数学期望:
两个随机变量的线性组合的方差:
第一问
cov = -0.32 * 0.1945 * 0.0213cov # -0.001325712
第二问
rate = [0.5, 0.5]income_e = 0.0504 * rate[0] + 0.0578 * rate[1]income_var = rate[0] * rate[0] * 0.1945 * 0.1945 + rate[1] * rate[1] * 0.0213 * 0.0213 + 2 * rate[0] * rate[1] * covincome_s = np.sqrt(income_var)print(income_e) # 0.0541print(income_s) # 0.0944
我们可以看到这种投资组合下,收益率为5.41%,风险大约在9.44%
第三问
rate = [0.2, 0.8]income_e = 0.0504 * rate[0] + 0.0578 * rate[1]income_var = rate[0] * rate[0] * 0.1945 * 0.1945 + rate[1] * rate[1] * 0.0213 * 0.0213 + 2 * rate[0] * rate[1] * covincome_s = np.sqrt(income_var)print(income_e) # 0.0563print(income_s) # 0.0371
我们可以看到这种投资组合下,收益率为5.63%,风险大约在3.71%
第四问
rate = [0.8, 0.2]income_e = 0.0504 * rate[0] + 0.0578 * rate[1]income_var = rate[0] * rate[0] * 0.1945 * 0.1945 + rate[1] * rate[1] * 0.0213 * 0.0213 + 2 * rate[0] * rate[1] * covincome_s = np.sqrt(income_var)print(income_e) # 0.0519print(income_s) # 0.1542
我们可以看到这种投资组合下,收益率为5.19%,风险大约在15.42%
第五问
组合(3)的资产组合的预期年收益率最高,且标准差最小,意味着风险低,毫无疑问组合(3)投资最优
第六问
个人偏好于将资金都投资于核心债券,从收益率的角度来看,债券的收益率是高于S&P500的,且风险小于它
连续
第三题 房产出售
某企业经理从芝加哥调动到亚特兰大,需要迅速出售她在芝加哥的房产。这位经理的雇主出价 210000 美元想要购买,截止日期是本周末。当前没有更好的报价,这位经理可以把房子保留至下月出售。与其经纪人沟通后得知,这位经理认为若把房子保留到下月出售的话,房价将服从 200000~225000 美元的均匀分布。
- 如果将房产保留到下月出售,写出售价的概率密度函数的数学表达式。
- 如果将房产保留到下月出售,她至少得到 215000 美元售房款的概率是多少?
- 如果将房产保留到下月出售,她得到的售房款少于 210000 美元的概率是多少?
- 是否应该将住房保留到下月出售?为什么?
第一问
第二问
p = (225 - 215) / (225 - 200) = 0.4
第三问
p = (210 - 200) / (225 - 200) = 0.4
第四问
如果比较在乎2500美元的话,可以将房子保留到下个月出售。
因为按照均匀分布的概率计算出来的期望为 (200 + 225) / 2 * 1000 = 212500 是高于210000美元的,值得一试
第四题 毕业生起薪
据美国高校和雇主协会报道,健康科学专业新大学毕业生的平均起薪为 51540 美元,商科新大学毕业生的平均起薪为 53901 美元(美国高校和雇主协会网站, 2015 年 1 月 5 日)。假设起薪服从正态分布,且健康科学专业新大学毕业生起薪的标准差为 11000 美元,商科新大学毕业生起薪的标准差为 15000 美元。
- 一名大学商科新毕业生的起薪至少为 65000 美元的概率是多少?
- 一名大学健康科学专业新毕业生的起薪至少为 65000 美元的概率是多少?
- 一名大学健康科学专业新毕业生的起薪低于 40000 美元的概率是多少?
- 若一名大学商科新毕业生的起薪比健康科学专业 99% 的新大学毕业生的起薪高,那么这名新毕业生的起薪至少是多少美元?
第一问
from scipy.stats import norm# 转化为标准正态分布z = (65000 - 53901) / 15000 # 0.73993print(1 - norm.cdf(z)) # 0.22967
根据计算结果可知,商科毕业生起薪至少为65000美元的概率约为23%
第二问
z = (65000 - 51540) / 11000 # 1.2236print(1 - norm.cdf(z)) # 0.11
根据计算结果可知,健康科学专业起薪至少为65000美元的概率为11%
第三问
z = (40000 - 51540) / 11000 # -1.049print(norm.cdf(z)) # 0.147
根据计算结果可知,健康科学专业起薪低于40000美元的概率约为14.7%
第四问
z = norm.ppf(0.99)salary = z * 11000 + 51540print(salary) # 77129.83
根据计算结果可知,该商科毕业生的起薪至少应为77130美元

