Numpy 科学计算

numpy 是 python科学计算的核心库。PYTHON里涉及到科学计算的包括Pandas,sklearn等都是基于numpy进行二次开发包装的。numpy功能非常强大，和scipy构建了强大的PYTHON数理计算功能，函数接口丰富复杂。

数组：Arrays

概念理解

• 同类型的序列数据
• 使用非负整数进行索引
• 维度的数量就是array的秩(rank)

创建数组

我们可以通过python的列表来创建array；通过方括号进行索引获取元素

一维数组创建

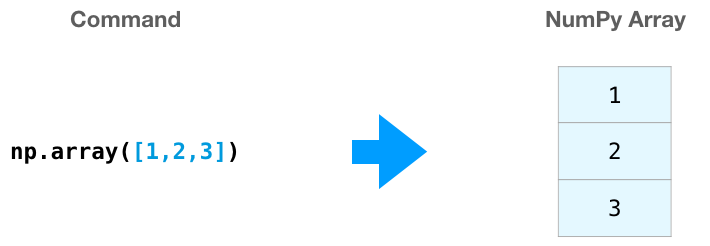
import numpy as np 
a = np.array([1,3,4,6,10])
print(a)                                        #   [1 2 3]
a.size                                            #   3
a.shape                                            #   (3,)
a[2]                                            #   同list的访问方式相同

注意，虽然打印数组时结果是横向输出的，但实际上是竖着排列的

另一方面，通过shape的结果也可以看出来，一个list时每一个元素就对应着一行，看图说话

高维数组的创建

不同维度之间使用逗号分隔，具体以二维数组举例来讲，从最外层的list到最内层的list，依次对应行数，列数，大list里的每一个小list都对应着一行

b = np.array([[1, 2, 3], [4, 5, 6]])
b.shape                                        # (2, 3)
b

执行

array([[1, 2, 3],
       [4, 5, 6]])

c = np.array([[[1, 2, 3, 4], [4, 5, 6, 7], [4, 5, 6, 7]], [[7, 8, 9, 10],[7, 8, 9, 10], [10, 11, 12, 13]]])
c.shape                                        # (2, 3, 4)

c

执行

array([[[ 1,  2,  3,  4],
        [ 4,  5,  6,  7],
        [ 4,  5,  6,  7]],

       [[ 7,  8,  9, 10],
        [ 7,  8,  9, 10],
        [10, 11, 12, 13]]])

依然是常规的方式进行选中，动手试一试。

c[1]

c[1,1]

c[1,1,2]

内置函数创建特殊数组

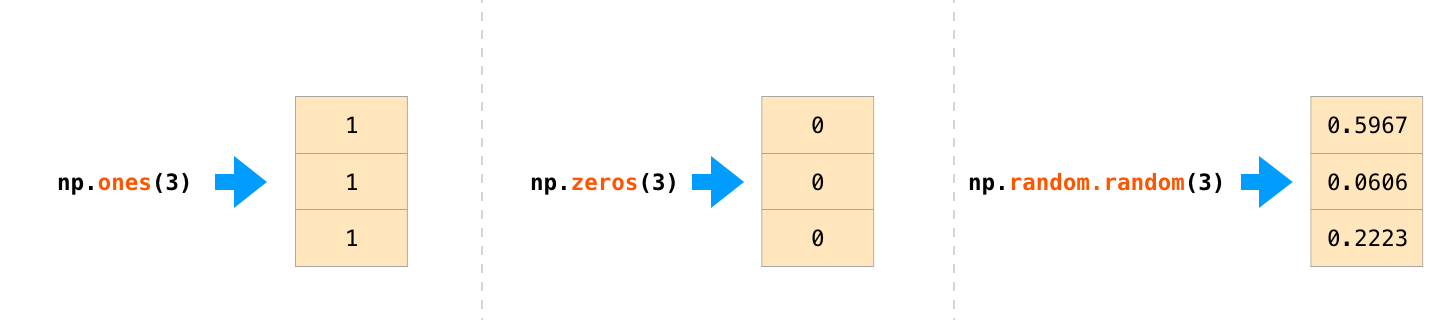
np.ones(3)
np.zeros(3)


b.shape
np.zeros_like(b)


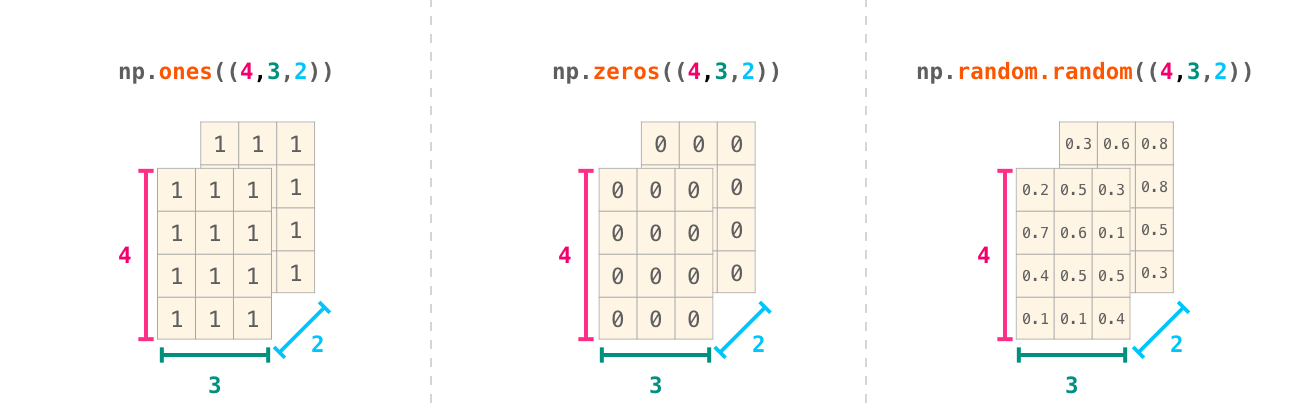
np.ones((4, 3, 2))
np.zeros((1,2,3))
np.random.random((1,2,3))


np.eye(3)

看一下eye函数的输出，还可以设置偏移的程度，具体可看函数说明。

array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])

Array的常用属性和方法

统计

a = np.random.randn(3,2)

a.size                                # 6                                

len(a)                                # 3

a.shape                                # (3, 2)

排序

axis参数指定在哪一个维度上进行排序，默认是最后一个维度

a

执行

array([[0.20859329, 0.40381061],
       [0.08943724, 0.16006834],
       [0.28924083, 0.49194053]])

在不指定axis参数的情况下，进行排序，此时最后一个维度为1

np.sort(a)

执行

array([[0.20859329, 0.40381061],
       [0.08943724, 0.16006834],
       [0.28924083, 0.49194053]])

指定axis参数为0，进行纵向的排序

np.sort(a, axis=0)

执行

array([[0.08943724, 0.16006834],
       [0.20859329, 0.28924083],
       [0.49194053, 0.40381061]])

指定axis参数为1，进行横向的排序

np.sort(a, axis=1)

执行

array([[0.20859329, 0.40381061],
       [0.08943724, 0.16006834],
       [0.28924083, 0.49194053]])

按照大小查索引

默认横向排序，只不过返回的是元素在原数组中的索引位置

a.argsort()

执行

array([[0, 1],
       [0, 1],
       [0, 1]])

条件查找

c = np.array([[10,20,30], [40,50,60]])
c

执行

array([[10, 20, 30],
       [40, 50, 60]])

来看一下二维数组c中大于45的元素有多少个?

np.where(c > 45)

执行

(array([1, 1]), array([1, 2]))

注意上面结果的输出，在c中大于45的元素总共有两个，分别对应的位置索引为(1, 1), (1, 2)；

轴0上的索引就为(1, 1)，轴1上的索引就为(1, 2)，分别对应着两个数组的输出。

np.where(c > 45, 2, 0)

执行

array([[0, 0, 0],
       [0, 2, 2]])

注意上面结果的输出，如果值大于45填充2，否则填充0

c > 25

执行

array([[False, False,  True],
       [ True,  True,  True]])

此时的输出是一个布尔数组，可以适当与中括号语法结合，进行元素的选取。

# c[c > 45]                          # 与下面的语句是等价的输出

c[np.where(c > 45)]                    # array([50, 60])

聚合计算

我们可以对数组应用常用的聚合函数

可以通过指定axis，表明函数在某个维度上进行计算

依旧使用上面的二维数组c

np.sum(c)                            # 210

np.max(c, axis=0)                # array([40, 50, 60])

np.std(c, axis=1)                # array([8.16496581, 8.16496581])

Shape改变

一个数组的 shape 是由轴及其元素数量决定的，它一般由一个整型元组表示，且元组中的整数表示对应维度的元素数。

我们最容易接触到的shape改变就是转置，这通常用于计算dot。

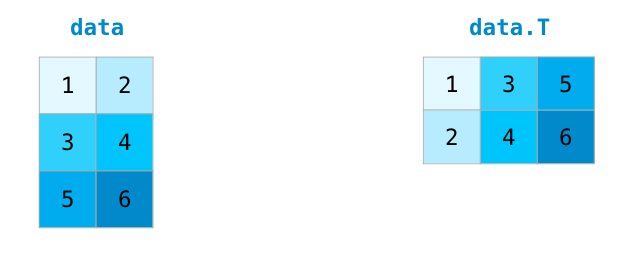
还有一种常见的情形是在机器学习中应用，我们需要改变数组的形状从而适应我们的建模需要

继续使用上面的二维数组c，c的shape是2行3列，我们来做一个转置操作。

c.T

执行

array([[10, 40],
       [20, 50],
       [30, 60]])

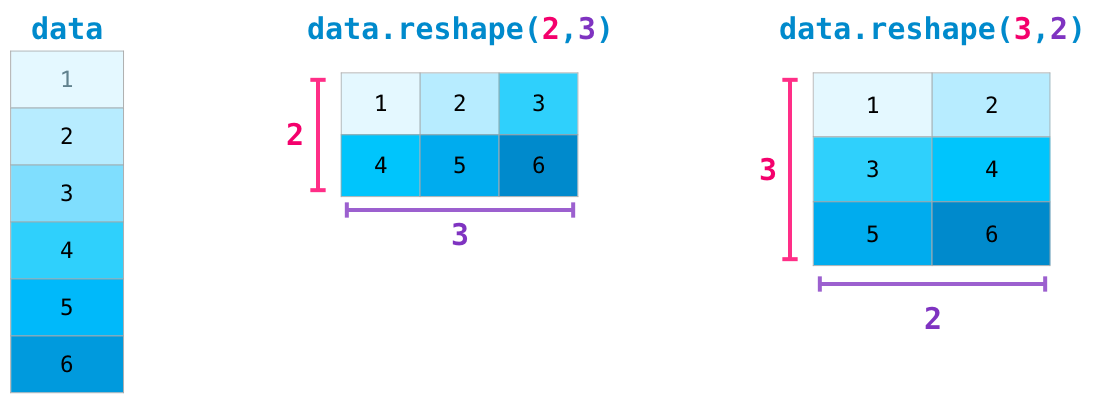
一个数组的 shape 可以由许多方法改变。

例如以下三种方法都可输出一个改变 shape 后的新数组，它们都不会改变原数组。

其中 reshape 方法在实践中会经常用到，因为我们需要改变数组的维度以执行不同的运算。

c.flatten()                    # array([10, 20, 30, 40, 50, 60])

c.ravel()                        # array([10, 20, 30, 40, 50, 60])

c.reshape(3, 2)

执行

array([[10, 20],
       [30, 40],
       [50, 60]])

如果在 shape 变换中一个维度设为 -1，那么这一个维度包含的元素数将会被自动计算。

如下所示，c一共有6个元素，在确定一共有2行后，-1会自动计算出应该需要3列才能安排所有的元素。

c.reshape(2, -1)

执行

array([[10, 20, 30],
       [40, 50, 60]])

随机数

numpy可以根据一定的规则创建随机数，随机数的使用会在后面概率论，数据挖掘的时候经常用到。

官方主页RANDOM

常用的一些方法：

• rand(d0, d1, …, dn) Random values in a given shape. Interval [0 , 1)
• randn(d0, d1, …, dn) Return a sample (or samples) from the “standard normal” distribution.
• randint(low[, high, size, dtype]) Return random integers from low (inclusive) to high (exclusive).
• random([size]) Return random floats in the half-open interval [0.0, 1.0).
• sample([size]) Return random floats in the half-open interval [0.0, 1.0).
• choice(a[, size, replace, p]) Generates a random sample from a given 1-D array

np.random.rand(2)                            # array([0.11982494, 0.68627288])
np.random.rand(2, 2)                        # 生成2行2列满足要求的二维数组

np.random.randn(3)                            # array([ 0.67585914, -0.381023  , -0.06518561])
np.random.randn(1,3)                        # array([[-0.69897368,  0.61978712,  1.53187008]])

np.random.randint(10)                        # 3
np.random.randint(1, 10, 3)                    # array([1, 9, 7])

np.random.random(2)                            # array([0.37545524, 0.63782397])
np.random.random((2, 3))                    # 生成2行3列满足要求的数组

np.random.sample((1,2))                        # array([[0.43636171, 0.91215752]])

np.random.choice([1,2,3,4,5], (3))            # array([5, 5, 1])
np.random.choice(10, 3)                        # array([5, 2, 7])
np.random.choice(10, (3, 2))                # 生成3行2列满足要求的数组

数组的索引

切片选取类似于list，可以使用单个索引位置或切片；但是array可以是多维度的，因此我们需要指定每一个维度上的操作

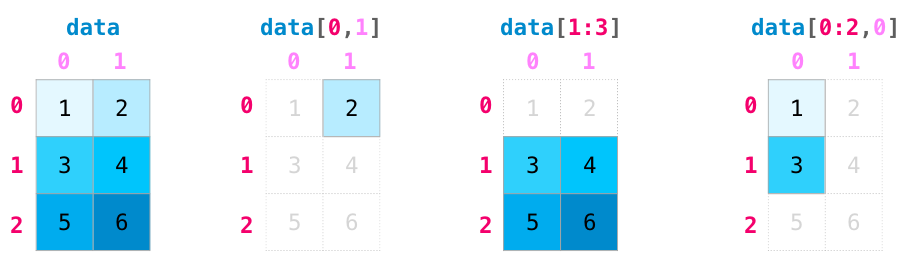
针对一维数组

a = [i for i in range(10)]                # [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

a[1]                                        # 1

a[2:3]                                        # [2]

针对多维数组

a = np.array(range(12)).reshape(3, 4)
a

执行

array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])

开始做数据选取练习

行的选取与列的选取用逗号隔开；行列自身的选取又可以通过切片[startstep]（前闭后开）

a[2]                                # 选中第三行    # array([ 8,  9, 10, 11])

a[1:5]                                # 选中第二行第三行，切片的方式

a[0::2]                                # 选中第一行和第三行，步长为2

a[:,2:]                                # 行全选，列选中后两列，结果为3行2列

a[:, 2]                                # 行全选，列为第三列

# 整数索引，使用tuple或list进行打包
a[(1,2), (0,1)]                        # array([4, 9])
a[[1,2], [0,1]]                        # array([4, 9])

# 布尔型索引
a > 5                                    # 输出为二维的布尔数组，大于5的值为True
a[a > 5]                                # array([ 6,  7,  8,  9, 10, 11])

数学计算

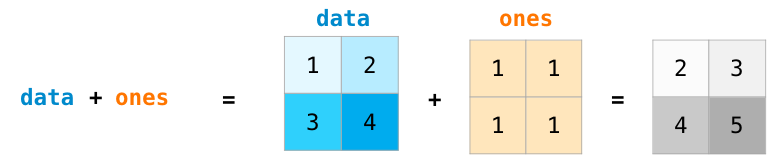
数组计算有广播机制，即使数组的形状不完全一样，也可以通过该机制进行计算

常规的计算：两个数组的shape相同

a = np.random.random((3, 4))
b = np.random.random((3, 4))

a + b

a - b

a * b

a / b

# 等价于上面的加减乘除
np.add(a, b)
np.subtract(a, b)
np.multiply(a, b)
np.divide(a, b)

非常规的计算：单个整数

a + 2

a * 2

点积运算（第一个矩阵的最后一维和第二个矩阵的第一维数量要相等）

a = np.array([1, 2])
b = np.array([[2,3], [4, 5]])
a.dot(b)                                        # array([10, 13])

求积是数组计算的最重要的形式！

具体计算逻辑如下所示：

实际应用

机器学习

在我们学习到后面机器学习的时候，会遇到一个公式。这个公式在统计学习中叫做最小二乘法，在机器学习的线性回归模型中叫做平方和误差

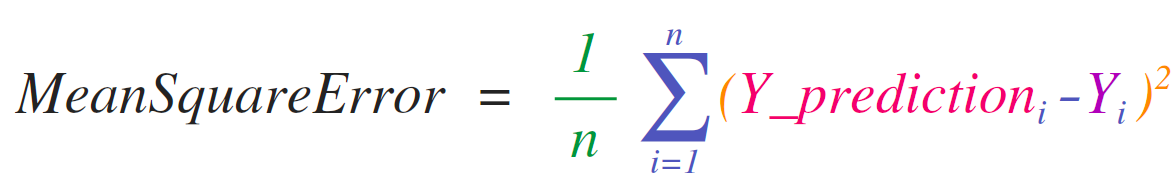
我们转换一下公式

设定一下lable和prediction

图像

我们在计算机保存一张灰色的图像使用的就是Numpy数组

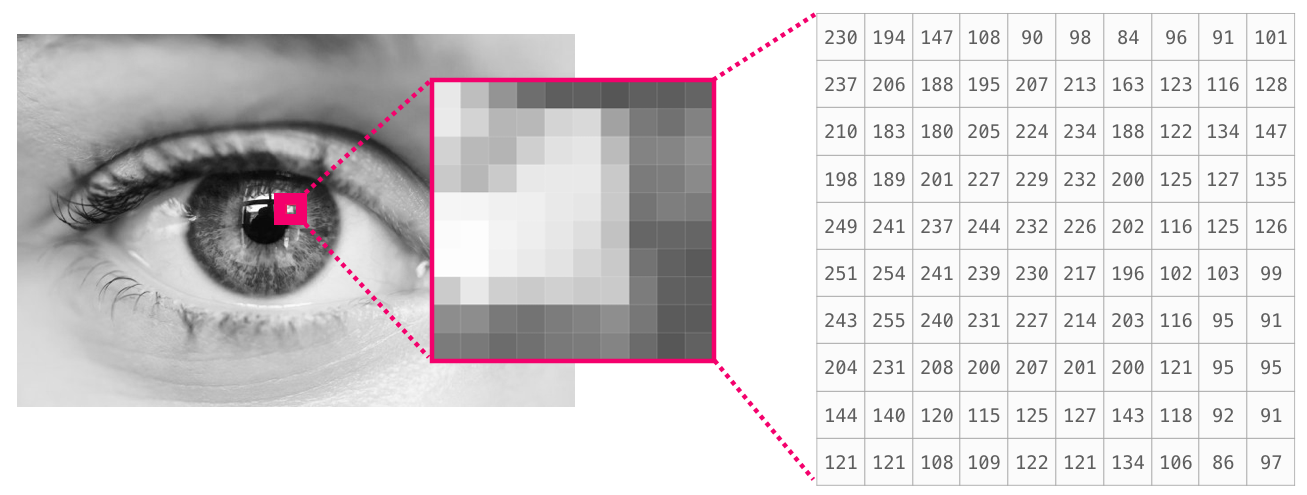
如果是彩色的图像，那么就是三维数组

文本

我们可以把一句话切割成单个的字符

然后可以用数字代表这些字符

但是通常这些id不会提供很多有用的信息，我们一般会根据某种算法，将它转换成向量形式