第一题 新生熟悉环境

在过去的几年里，Lakeland 大学发现一年后离开的大学生比例有所增长。去年 Lakeland 大学开始启动一项自愿参加的新生熟悉环境活动，该项活动为期一周，其目的是帮助一年级大学生调整自己在大学校园的生活。如果Lakeland 大学能证明，新生熟悉环境活动对保留大学生不流失有一个正面的影响，那么校方将考虑面向全体一年级大学生实施新生熟悉环境活动。Lakeland 大学的行政部门还猜想:GPA 比较低的大学生，在一年后离开 Lakeland 大学的可能性比较大。为了研究这些变量与保留大学生不流失的关系，Lakeland 大学从去年进校的大学生中抽取了 100 名学生组成一个随机样本。这些数据被存放在为 Lakeland 的数据集里，部分数据如下表所示：

大学生 GPA 新生熟悉环境 留在学校
1 3.78 1 1
2 2.38 0 1
… … … …
100 3.85 1 1

如果大学生在二年级仍然留在 Lakeland 大学，则因变量 y 被赋值为 1; 否则，y=0。两个自变量如下所示：
image.png

  1. 写出 y 关于 x1 和 x2 的 logistic 回归方程。
  2. 当 x2 = 0 时，怎样解释 E(y) ？
  3. 利用两个自变量和 Python 计算估计的对数机会比。
  4. 在 a=0.05 的显著性水平下，进行总体的显著性检验。
  5. 在 a=0.05 的显著性水平下，检验每一个自变量是否显著。
  6. 利用在(3)中得到的估计的对数机会比，对于 GPA 为 2.5，而且没有参加新生熟悉环境活动的大学生，估计他们在二年级仍留在 Lakeland 大学的概率。对于 GPA 为 2.5，并且参加新生熟悉环境活动的大学生，概率的估计值是多少?
  7. 新生熟悉环境活动的机会比率的估计值是多少？对这个估计值进行解释。
  8. 你是否建议把新生熟悉环境活动作为一项必须参加的活动？为什么？
  1. import pandas as pd
  2. import statsmodels.api as sm
  4. df = pd.read_csv('Lakeland.csv')
  5. df.head()

看一下数据的轮廓：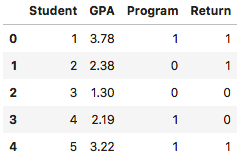
image.png

第一问

我们通过 unique 函数查看 Program 列数据都为0，1；为 int64 类型；且不存在无效值；直接应用模型。

  1. x = df[['GPA', 'Program']]
  2. y = df['Return']
  4. x = sm.add_constant(x)
  5. model = sm.Logit(y, x).fit()
  6. print(model.summary2())

执行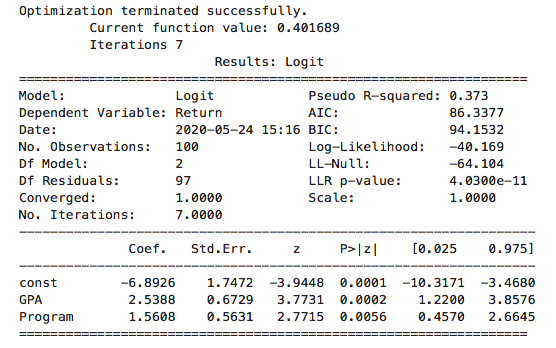
image.png
我们估计的logistic回归方程公式为：多元线性回归习题 - 图4

代入我们求解出来的参数可得：多元线性回归习题 - 图5

第二问

当x2=0时，表示对于没有参加这个活动的大一新生，一年后留在大学的期望（即概率）与GPA之间的关系。

第三问

估计的对数机会比为：多元线性回归习题 - 图6

第四问

在 a=0.05 的显著性水平下，进行总体的显著性检验。回忆下总体参数显著性检验：原假设为两个模型参数相等且等于0；备择假设为两个模型参数至少有一个不等于0。
从前面的打印输出，我们可以看到统计量的p值为 4.0300e-11 很明显该值小于 0.05。因此在0.05的显著性水平下，我们可以拒绝原假设，并且得出模型的总体是显著的结论。

第五问

在 a=0.05 的显著性水平下，检验每一个自变量是否显著。
从前面的输出我们可以看到，自变量GPA对应的p-value为0.0002，自变量Program对应的p-value为0.0056，都是小于0.05的；因此在0.05的显著性水平下，两个自变量与因变量的关系在统计上都是显著的。

第六问

  1. tmp = np.e ** (-6.8926 + 2.5388 * 2.5 + 1.5608 * 0)
  2. p1 = tmp / (1 + tmp)
  3. print(p1)                        # 0.367
  5. tmp = np.e ** (-6.8926 + 2.5388 * 2.5 + 1.5608 * 1)
  6. p2 = tmp / (1 + tmp)
  7. print(p2)                       # 0.734

因此，对于 GPA 为 2.5，而且没有参加新生熟悉环境活动的大学生，估计他们在二年级仍留在Lakeland大学的概率 36.7% ；对于 GPA 为 2.5，但参加新生熟悉环境活动的大学生，估计他们在二年级仍留在Lakeland大学的概率 73.4%。

第七问

  1. odds = np.e ** 1.5608 
  2. print(odds)                        # 4.76

因此，新生熟悉环境的机会比率的估计值是4.76。即当其它自变量保持不变时，新生熟悉环境的机会比是不熟悉环境机会比的4.76倍。

第八问

建议把新生熟悉环境活动作为一项必须参加的活动。首先该自变量对应的机会比率为4.76，大于1，很明显对总体的机会比率有一个正影响；另外，前面也已经验证了该自变量与二年级是否退学在统计上是显著的。从95%的置信区间也可以看出来。（95%的置信区间[0.457, 2.6645]不包含值0，因此可拒绝多元线性回归习题 - 图7的原假设）

第二题

美国能源部和环境保护署的《2012燃油经济指南》提供了2012年汽车和卡车的燃油效率数据。名为2012FuelEcon 的文件提供了 309 辆汽车的部分数据。其中，列标题的含义如下所示：
 列标题 Manufac-turer 表示生产汽车的公司名称;
 列标题 Displace-ment 表示发动机排量(升);
 列标题 Fuel 表示要求或建议的燃料类型(普通汽油或优质汽油);
 列标题 Drive 表示驱动器的类型(F 为前轮驱动，R 为后轮驱动，A 为四轮驱动);
 列标题 HwyMPG 表示在高速公路上行驶的燃油效率额定值(单位:英里/加仑)

  1. 建立一个估计的回归方程，使该方程在汽车的发动机排量已知时，能用来预测该车在高速公路上行驶的燃油效率额定值。在 a=0.05 的显著性水平下，检验估计的回归方程的显著性。
  2. 考虑增加一个虚拟变量 FuelPremium。如果汽车要求或建议的燃料类型是优质汽油，则 FuelPre-mium 的值为 1；如果汽车要求或建议的燃料类型是普通汽油，则 FuelPremium 的值为 0。建立一个估计的回归方程，使该方程在发动机排量和虚拟变量 FuelPremium 已知时，能用来预测汽车在高速公路上行驶的燃料效率额定值。
  3. 在 a=0.05 的显著性水平下，确定在(2)中增加的虚拟变量是否是显著的。
  4. 考虑增加虚拟变量 FrontWheel 和 RearWheel。如果是前轮驱动汽车，则 FrontWheel 的值为 1；否则，FrontWheel 的值为 0。如果是后轮驱动汽车，则 RearWheel 的值为 1；否则，RearWheel 值为 0。于是，如 果是四轮驱动汽车，则 Front-Wheel 和 RearWheel 的值都为 0。建立一个估计的回归方程，使该方程在发动机排量、虚拟变量 FuelPremium 以及虚拟变量 FrontWheel 和 RearWheel 已知时，能用来预测汽车在高速公路上行驶的燃料效率额定值。
  5. 在 a=0.05 的显著性水平下，对在(d)中得到的估计的回归方程，检验总体的显著性和每一个自变量的显著性。
  1. from statsmodels.formula.api import ols
  2. df = pd.read_csv('2012FuelEcon.csv', header=0, names = ['Manufacturer', 'Displacement', 'Fuel', 'Drive', 'MPG'])
  3. df.head()

先看一下数据的轮廓：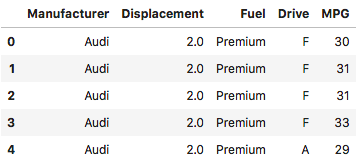
image.png

第一问

  1. model1 = ols('MPG ~ Displacement', data=df).fit()
  2. model1.summary()

执行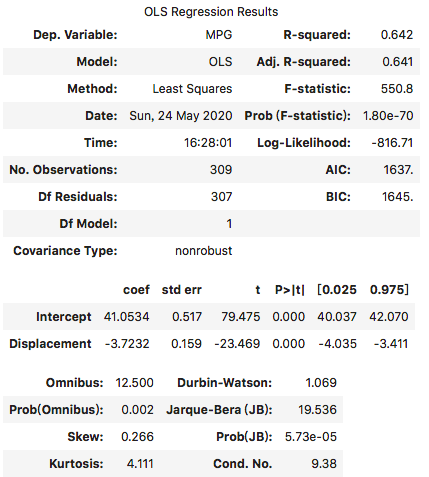
image.png
根据上面的输出，我们可以得出估计的回归方程如下所示：多元线性回归习题 - 图10
我们看到Displacement这一行所对应的p-value值为0.000，是小于显著性水平0.05的。因此，我们可以拒绝原假设，得出该估计的回归方程在统计上是显著的。

第二问

  1. # 查看是否有不符合要求的数据
  2. # type(df['Fuel'][0])
  3. # df['Fuel'].unique()
  4. # sum(df['Fuel'].isna())
  6. # 建立关于汽车的发动机排量和燃料类型的估计回归方程 其中燃料类型为虚拟变量 1表示优质汽油 0表示普通汽油
  8. def fuel_dummy(s):
  9.     if s == 'Premium':
  10.         return 1
  11.     elif s == 'Regular':
  12.         return 0
  14. df['FuelPremium'] = df['Fuel'].apply(lambda s: fuel_dummy(s))
  15. df.head()

执行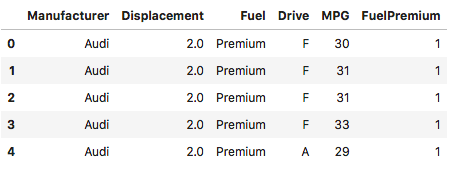
image.png

  1. model2 = ols('MPG ~ Displacement + C(FuelPremium)', data=df).fit()
  2. model2.summary()

执行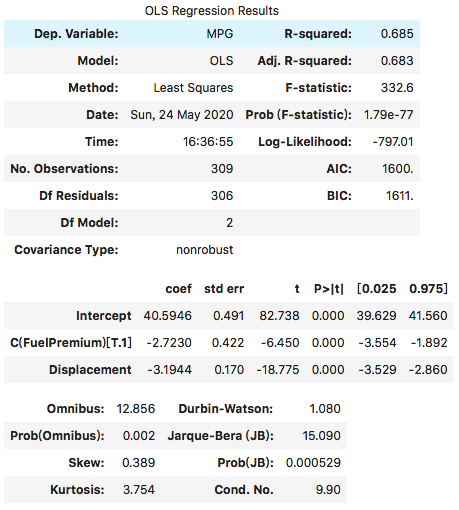
image.png
根据上面的输出，我们可以得出估计的回归方程如下所示：
多元线性回归习题 - 图13

第三问

我们看到上面的输出，计算出来的p-value直接就是大于统计量的绝对值的，也就是我们不用再额外乘以2了。（我们心里要明白，这里进行的t检验是双侧检验）在新增的分类变量 FuelPremium 这一行，对应的p-value接近于0，因此在0.05的显著性水平下，我们得出结论，该虚拟变量与因变量的关系在统计上是显著的。

第四问

  1. # 检查数据完整性
  2. # df['Drive'].unique()
  3. # sum(df['Drive'].isna())
  5. # F表示前轮驱动
  6. df['FrontWheel'] = df['Drive'].apply(lambda s: 1 if s == 'F' else 0)
  7. # R表示后轮驱动
  8. df['RearWheel'] = df['Drive'].apply(lambda s: 1 if s == 'R' else 0)
  9. df.head()

执行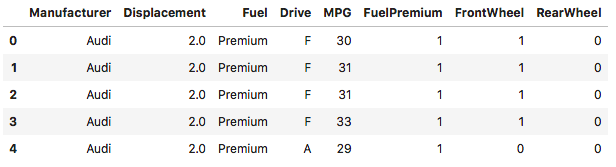
image.png

  1. model3 = ols('MPG ~ Displacement + C(FuelPremium) + C(FrontWheel) + C(RearWheel)', data=df).fit()
  2. model3.summary()

执行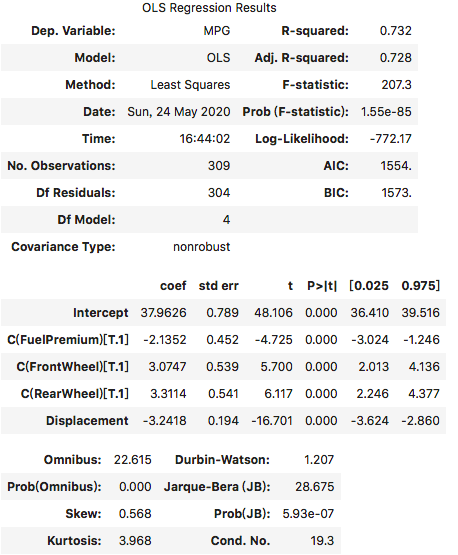
image.png
根据上面的输出，我们可以得出估计的回归方程如下所示：
多元线性回归习题 - 图16

第五问

对在(d)中得到的估计的回归方程，检验总体的显著性和每一个自变量的显著性。从上面的输出，我们看到F检验对应p-value为1.55e-85, 小于显著性水平0.05；因此得出结论：总体上是显著的。
我们看到每一个自变量所在行对应p-value基本上为0，这也小于显著性水平0.05，因此得出结论：每一个自变量与因变量在统计上也都是显著的。