介绍
前言
虽然名称里带有Regression字样,看起来像是回归模型,但实际上它是一个分类模型。大部分情况下是二分类模型,但某些情况下也可作多分类。
定义
二分类模型,目标值为0/1。即只有两种结果,是或不是,成功或失败等;工作生活中很常见。
模型结果值在(0, 1)之间,表达的是概率值。通过与阈值进行比较(默认的阈值大小为0.5),判断当前的样本属于哪一个类别;结果值无限接近于0和1,但永远不会等于0和1;默认模型吐出的是正样本的概率,即为类别1的概率。(比如某个样本预测的模型结果值为0.7,同时我们设置的阈值为0.5,0.7大于阈值,因此模型预测该样本是属于类别1)。
公式

解释:其中θ还是参数, 表示矩阵的转置,x为输入的特征,括号中是矩阵乘法。logistic regression 是将 linear regression 的结果做了一层转换,对比函数g(z),味道很是明显。

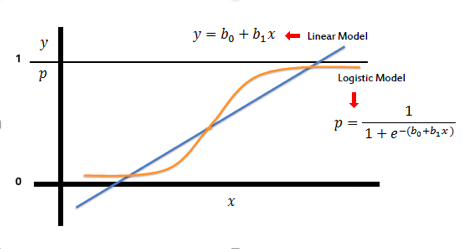
与线性回归的联系
logistic regression 和 linear regression 都是线性模型。什么是线性模型,就是可以通过一条直线来表达的模型。logistic regression是线性分类模型,通过一条直线区分开来样本的类别。linear regression是线性回归模型,通过一条直线来拟合样本数据。
代价函数
强假设
我们假设样本之间是相互独立的,这样方便进行概率间的乘法运算,应用 。
似然函数
利用已知的样本信息,反推出最有可能产生当前这种样本的模型参数。知道了每一个样本发生的概率如何表示,那么我们抽样产生当下的这个全体样本的概率为多少呢?使用连乘符号, 将它们相乘即可,因为我们已经假设样本之间是相互独立的,相乘得到的结果,可称之为似然函数。
令似然函数取得极大值(极大似然估计),此时求解出来的模型参数 可能性最大。(即这种情况求解出来的
最有可能产生当下这种情况的样本),极大似然估计之后,在函数最外层添加个负号,就得到了代价函数。(就函数的极大值,和在函数前面添加负号后求解极小值,两者是等价的)
插入知识
对于连乘的情况求极值,我们通常的做法是取对数。因为单纯加上对数,函数的单调性并未发生变化。想一想对加法求导肯定比对乘法求导方便的多呀。
在等式左边,a为底数,x为真数
公式推导
假设x,θ是已知的情况下,我们可以应用到条件概率。因为最终结果的类别值要么为0,要么为1,两者的概率值相加和为1,因此类别值为1或者0的概率可以如下这样所示:
我们想办法把上面两个式子写到一个式子上:(下面式子中y取值1或者0时,分别与上面两式对应)
那么一个具体样本的概率该如何表示呢?代入 :
我们再给它加个连乘符号,表示产生当前所有样本的可能性:(下面这个式子即为我们的似然函数)
对上式等号右边取对数,连乘转连加,函数单调性保持不变,可得:
最终我们logistic regression的代价函数如下所示:(与上式基本相同,只不过多了个系数-1/(2m))
解释一下,上式的负号是怎么来的?我们想要似然函数取得极大值,这与添加上符号取得极小值,是等价的。
对比一下linear regression的代价函数:
模型评估-准确率accuracy
案例
一个班级有100个学生,某次考试过后,老师使用LR模型根据学生的历史表现和成绩预测他们本次考试通过的几率是多少。模型预测其中90个学生通过考试,10个学生没有通过。在成绩单出来之后发现,其中95个学生通过,5个学生没有通过。我们用1代表没通过,0代表通过。
这里说明一下:我们为什么使用类别1来代表“没通过”,老师的目的是干嘛?老师的目的是为了找出可能没有通过考试的学生(在样本中占比较少的那个类别),而不是寻找通过考试的学生(在样本中占比大)。找到这些可能没通过考试的学生后,老师就可以采取进一步措施了,比如提前谈话,叫家长等。而如果是找到通过考试的学生,这占绝大多数,没什么意义,也没什么措施可做。
举例子:比如说银行的征信系统,目的是找出信用不好的那部分人,即找出样本数量少的那个类别的人,大部分都是信用良好的人,知道极少数几个信用差的人之后,银行就可以采取措施,不贷款给他们或贷款时添加附加条件等。公安的罪犯系统也是一样的道理,模型关注的是少数有犯罪记录的人,而不是大多数的好人。
混淆矩阵
下图所示的矩阵,学名就称之为混淆矩阵。(confusion matrix),有点像联合概率表。

accuracy概念
预测的和实际情况匹配的部分属于是模型预测正确的样本。即使用预测正确的样本数量除以总的样本数量就是模型预测的正确率。比如在案例中,预测没通过,实际也没通过,5个学生满足,预测通过,实际也通过,90个学生满足,因此该模型的正确率为 。
弊端
假设模型预测100个学生的及格情况如下所示,真实是90个及格,10个不及格,LR模型预测的结果为100个学生都及格。在这种情况下模型准确率accuracy达到了90%,很明显,但从准确率而言,这个模型是不错的,但却是没什么价值的,因为该模型并没帮老师找出任何一个不及格的学生。面对这个结果,老师什么行动也做不了。

尤其是样本不均衡的情况下,即某一类别样本数量特大,另一类别特小,accuracy并不是一个好的衡量模型的指标,那到底该怎么衡量模型的好坏程度呢?欢迎进入下一小节。
Precision 与 Recall
Precision 精确率

理解:预测情况下,所关心类别的总预测样本数量中有多少是正确的。即该类别下正确了多少个样本 / 总的该类别下预测的样本数量。可通俗理解为预测对了多少。
举例:比如模型预测结果中有10个样本是正确的,如果真实情况是只有5个样本正确,则精确率为50%;如果真实情况有10个样本正确即匹配,则精确率为100%;如果真实情况有15个样本正确,精确率依然为100%;
Recall 召回率
概念:真实情况下,所关心类别的总真实样本数量中有多少是正确的。即该类别下正确了多少个样本 / 总的该类别下真实的样本数量。可通俗理解为真实情况下所属类别的样本当中捞回了几个。
举例:比如真实情况下有10个样本为正确的。模型预测了5个为正确的,召回率为50%;模型预测了10个为正确,召回率为100%;模型预测了15个位正确,召回率依然为100%。
案例应用

根据上面这个模型的预测结果,我们可以计算出:
Precision精确率为 Recall召回率为

同样的,根据这个模型的预测结果,我们可以计算出:
Precision精确率为 Recall召回率为
这样一来,两个模型的高低立下显而易见了。有一点我们需要注意:无论是计算Precision还是Recall,我们的分子都是一样的,只有分母发生了变化。
PR曲线
根据Precision和Recall作出来的图,称之为Precision-Recall图,图中的曲线称之为PR曲线。

Precision越大,Recall越小;而Recall越大,则Precision越小;它们彼此之间是相互制衡的关系。下方围成的面积称为PR Area,面积越大,说明模型预测的越好,此时的Precision和Recall值达到了最佳状态。
阈值的划分
举例
在实际的工作应用中,我们一般不会采用0.5直接作为阈值,进行类别的划分,为什么呢?看下面两个案例:
公安抓犯罪嫌疑人,追求高的精确率,不可能100个嫌疑犯都抓回来,只要在把握比较大的情况下才采取抓捕行动,也就是说预测正确的样本中追求尽可能多的样本是真实正确的。因此需要设置较高的阈值,比如说0.9等。
银行贷款,银行会尽可能的避免贷款给可能欠钱不还的人,如果100个人中有两三个人信用不好,银行可能是这100个人都不发放贷款。属于是“宁可错杀,也不放过”,不追求高的精确率,即低的精确率,高的召回率。因此需要设置较低的阈值,比如说0.3等。
影响
阈值的不同,会导致模型预测的所属类别可能不同,虽然模型吐出的概率值本身没有发生变化,但划分类别的依据已经发生了变化。进而混淆矩阵发生变化,进而与之对应的Precision和Recall计算结果也发生变化。
PR曲线画法
我们可以设置不同的阈值,每个阈值对应着一个混淆矩阵,每个混淆矩阵进而对应着一对Precission和Recall值。横轴为Recall,纵轴为Precision,即可画出散点图,如果阈值划分的足够细,比如0.1等,散点足够多,那么连线后可以得到一条平滑的曲线。
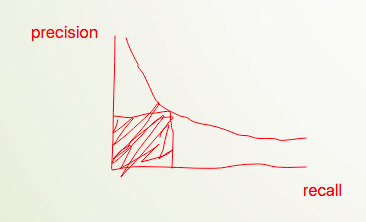
可以看到Precision和Recall是相互制衡,曲线上的每一个点都对应着一个具体的阈值。我们追求的是某一阈值即某一点下Precision和Recall围成的面积最大,这需要用到微积分的知识,那有没有其它方式呢?比如用一个指标直接来衡量precesion和recall之间达到了一个最佳状态,即面积最大呢?答案是存在的。
混淆矩阵
文字描述

矩阵中的元素:TN(True Negative)、FP(False Positive)、FN(False Negative)、TP(True Positive),参照我们之前的例子很容易理解,Predicted Yes 和 Actual Yes 表示类别1,Predicted No 和 Actual No 表示类别0。在矩阵内部,N表示预测结果类别值为0,P表示预测结果类别为1,T和F则是根据是否与真实情况一致决定的。
中间指标
F1 score
我们可以用“F1 score”这个指标进行衡量,面试的时候常问到,它与Precision和Recall的关系是怎样的?
F1 score是 Precision 和 Recall 的调和平均数。
调和平均数(harmonic mean)又称为倒数平均数,是各变量倒数的算术平均数的倒数。简单来说,就是倒数求平均,然后再倒一次,计算公式为 。计算Precision和Recall的调和平均数,结果即为F1 score。

ROC曲线
直观描述
横坐标:1 - Specificity, 称为伪正类率(False Positive Rate,对应上图中的FPR),预测为正但实际为负的样本占所有负样本的比例。(其中Specificity对应上图中SPC or TNR)。计算方式为:FP / (TN + FP)。
纵坐标:Sensitivity,称为真正类率(True Positive Rate,对应上图中的TPR,也叫Recall),预测为正且实际为正的样本占所有正样本的比例。计算方式为:TP / (FN + TP)。

上图中的三条实线分别对应三种不同的二分类模型所绘制的ROC曲线。
如何绘制
在一个LR的二分类模型中,其给出的是每一个实例为正类的概率。我们可以通过设置不同的阈值计算出多组(FPR, TPR),从而绘制出散点图。和我们绘制PR曲线是类似的思路。
ROC曲线维基百科的定义:A receiver operating characteristic curve, i.e. ROC curve, is a graphical plot that illustrates the diagnostic ability of a binary classifier system as its discrimination threshold is varied. (这里的discrimination threshold可翻译为阈值)。
分类器输出的是样本属于正样本类别的概率,我们根据每个测试样本属于正样本的概率值从大到小排序。这些概率值就会成为discrimination threshold(阈值)。通过一个案例来说明:
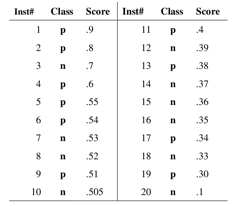
如上图的20个样本组成的案例所示:我们从高到低按照score值(即每个测试样本预测为正样本的概率)进行排序,然后依次将不同的score值作为阈值,当测试样本大于等于该值,我们就判定为正样本,否则为负样本。每次取不同的阈值,就会产生不同的混淆矩阵,进而计算出不同的FPR和TPR组合。

解释:上图中的每个点对应着一个阈值,也对应着一组(FPR, TPR),当阈值设置为0时:所有的样本均被预测为正样本,不存在预测为负的样本,即 TN 和 FN 的值都为0,对应点(1, 1);当阈值设置为1时:所有的样本均被预测为负样本,不存在预测为正的样本,即 TP 和 FP 的值都为0,对应点(0, 0);阈值取值越多,ROC曲线就越平滑。
横坐标: 纵坐标:
AUC (最常用,面试必考)
AUC(Area Under Curve),代表ROC曲线下方的面积,AUC值越大代表模型效果越好。
从AUC判断分类器的优劣标准:AUC = 1,完美分类器,采用这个预测模型时,存在至少一个阈值能得出完美预测。实际应用中基本大不可能存在,如果很接近于1,大多是过拟合;0.5 < AUC < 1,优于随机猜测,这个分类器(模型)妥善设定阈值的话,能有预测价值;AUC = 0.5,跟随机猜测一样,模型没有预测价值;AUC < 0.5,比随机猜测还差,模型很烂;一般经验是在0.7左右就不错了,不绝对,不固定的。

Why ROC
难道有了Precision和Recall还满足不了要求?是的,在下图中,a,c代表ROC曲线,b,c代表P-R曲线。a,b是源数据(均衡)测试,c,d是负样本扩大十倍测试。ROC曲线可以更好的处理样本不均衡的情况,而Precision和Recall曲线会因为样本不均衡而曲线畸形。
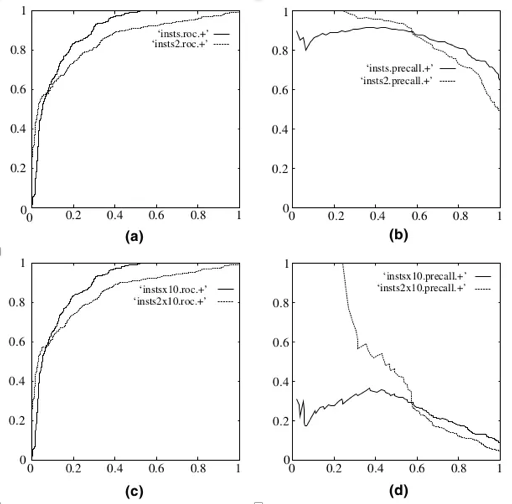
比较PR曲线的Precision和ROC曲线的FPR(它们两个另外一个轴的度量都为Recall),回忆一下计算方式:
Precision的分母含义为预测为正实际为正的和预测为正实际为负的样本和,正负样本混合在一起,分子为预测为正实际为正的样本数量,表示的含义为:预测的正样本中有多少是正确的?FPR的分母是实际为负的全部样本,分子是预测为正实际为负的样本,表示的含义为:实际为负的样本中有多少是预测正确的?一个是从预测的角度进行考虑,一个是从实际角度基于同一类样本,即负样本进行考虑。