假设检验(P205)
原假设
- 对总体参数做一个尝试性的假设(原假设称为 H)(null hypothesis)
备择假设
- 与原假设的内容完全对立的假设 (备择假设称为 H)(alternative hypothesis)
建立假设的依据
- 一般情况下我们是先确定备择假设,后确定原假设
- 一般将检验试图建立的结果,即目的作为备择假设
- 举例
- 将研究中的假设作为备择假设
- 比如我们研究了一种新型燃料系统,比原来的燃料系统平均24英里/加仑更好。则备择假设为
- 将受到挑战的假设作为原假设 (利用假设检验对某种假定提出质疑)
- 比如听装可乐宣称至少为67.6盎司,我们想根据样本证明是小于67.6盎司的。则备择假设为
假设检验类别
- 单侧检验
- 上侧检验
- 下侧检验
- 双侧检验
对于总体均值的假设检验,我们令 代表假定值并且必须采用以下三种形式之一进行检验:
  
前两种形式被称为单侧检验,第三种形式被称为双侧检验。
注意:等号总是出现在原假设中。因此双侧就只能有一种写法。
Type 1 & Type 2
- 引入
- 由于假设检验是基于样本信息得到的
- 不可能结论总是正确,必须考虑存在的误差
- 第一类错误
- 原假设为真却拒绝了原假设
- 第二类错误
- 原假设为假却接受了原假设
- 总结
- 犯的错误都是与原假设有关的
- 拒绝了,一定会产生第一类错误
- 接受了,一定会产生第二类错误
- 只不过这个错误的接受率和概率是多大
- 显著性水平
- 原假设为真并且以等号形式出现时犯第一类错误的概率
- 注意一个词:概率
- 如何选取
- 犯错成本高的话,就选取小的概率
- 犯错成本低的话,可以选大的概率
- 这里的成本是结合具体的业务来考虑的
- 显著性检验
- 只控制第一类错误的假设检验称为显著性检验
- 这里的假设检验并没有对第二类错误进行控制
- 因此统计学家建议,只使用
- 两个结论
- 拒绝原假设
- 不能拒绝原假设
- 如果结论是接受原假设,那么则需要评估犯第二类错误的概率

这里想对显著性水平解释一下,即需满足以下三个条件:实际原假设为真,以等号形式出现,但结论认为原假设为假;可以认为显著性水平是我们可容忍犯 Type 1 错误的最大概率。
均值检验(总体标准差已知)(P209)
总体均值的单侧检验
- 下侧检验
- 备择假设小于总体均值
- 原假设大于等于总体均值
- 上侧检验
- 备择假设大于总体均值
- 原假设小于等于总体均值
- 显著性水平
- 通常由决策者直接决定,一般取0.05
- 检验统计量
- 通过样本均值的抽样分布
- 转化为z-score(即标准正态分布)计算概率
- (样本均值 - 总体均值) / 样本的标准误差
- 样本的标准误差 = 总体的标准差 / 样本容量开根号
- 抛出问题
- 检验统计量达到多少时,或者说与总体均值差多少时
- 我们才能说差异明显呢
- 我们才能甘愿冒着犯第一类错误的概率拒绝原假设呢
案例应用:
美国联邦贸易委员会(FTC)定期设计统计调查,用以检验制造商的产品说明。大号听装Hilltop咖啡的标签上标明装有3磅/听。FTC把大号听装咖啡标签上的信息理解为Hilltop的承诺:听装咖啡重量的总体均值为3磅/听。我们将说明,FTC如何通过下侧检验来验证Hilltop的承诺。
设定假设:
显著性水平:设定显著性水平为0.01
假设选取样本的数据均值小于总体均值的估计,那么就要拒绝原假设。我们想要知道的是当样本均值比3磅少多少的时候,我们才能断言差异明显,并且甘愿犯第一类错误的风险控告Hilltop没有信守承诺。这个问题中,一个关键因素就是决策者选取的显著性水平。
计算检验统计量:
已知听装咖啡重量的总体标准差为0.18,此次抽取的样本容量为n=36,套用抽样分布小节中已知总体标准差情况下求标准误差的公式,即 ,样本均值的分布形态如下图所示:

一般步骤
- 设定假设
- 选取显著性水平
- 计算检验统计量
p值法&临界值法
- p-值法
- 概念
- p值首先是一个概率值
- 它度量样本所提供的证据对原假设的支持程度
- p值越小,说明拒绝原假设的证据越多
- 大白话
- p-值就是犯第一类错误的概率(实际显著性水平)
- p-值越小,检验统计量与总体参数差异性越大,即越显著,推翻原假设的证据越足(等号位于原假设中)
- 对于下侧检验
- p值是检验统计量小于等于样本所给出检验统计量的概率
- 对于上侧检验
- 为大于等于
- 拒绝法则
- 如果p-值小于等于a,则拒绝原假设
- 概念
- 临界值法
- 概念(针对下侧检验而言)
- 在检验统计量的分布中
- 与下侧面积a相对应的值是检验统计量的临界值
- 换句话说,也是拒绝原假设的样本检验统计量的最大值
- 拒绝法则
- 如果样本检验统计量小于等于z(a),则拒绝原假设(下侧)
- 为大于等于(上侧)
- 概念(针对下侧检验而言)
案例解决: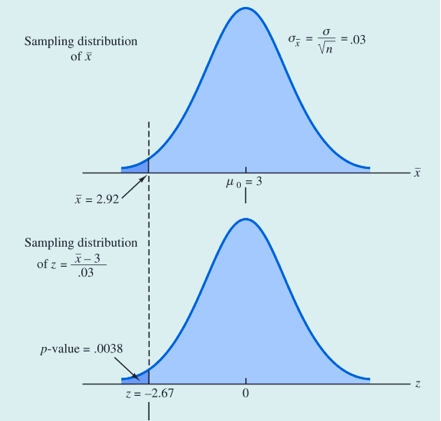
p-值法:
对于下侧检验, p-值是检验统计量小于或等于样本所给出的检验统计量的值的概率,因此必须得到标准正态分布曲线下在检验统计量的值左边部分的面积。我们抽取的36听咖啡样本均值 = 2.92磅。计算检验统计量
。从而p-值为检验统计量小于或等于-2.67的概率。
from scipy.stats import norm# 直接对应下侧面积p_value = norm.cdf(-2.67)print(p_value) # 0.00379
利用标准正态概率分布表,我们可知z= -2.67下侧的面积为0.0038. 那么这个值足以能够使得我们拒绝原假设么?答案是依赖于检验的显著水平。我们之前选取0.01为显著性水平,那么由于0.0038小于0.01,故我们拒绝原假设,从而在0.01的显著性水平下我们发现有足够的统计证据拒绝原假设。(风险在可控范围内)
虽然在这个例子中,我们拒绝了原假设,但我们仍然是有可能犯第一类错误的,只不过这个概率很小,为0.0038,在我们可以容忍的范围内(即显著性水平为0.01,而0.0038 < 0.01)。假设我们抽取的样本均值为2.99,从而通过样本统计量计算出来的p-value肯定是大于0.01的,要么重新抽样,要么考虑第二类错误,因为对于大于显著性水平的样本,算不上是有力的证据,我们也不能依此作出任何决定。
临界值法:
对于下侧检验,临界值是确定检验统计量的值是否小到足以拒绝原假设的一个基准。在检验统计量的抽样分布中,与下侧面积 相对应的值是检验统计量的临界值。换句话说,下侧检验中,临界值是使得我们拒绝原假设的检验统计量的最大值。
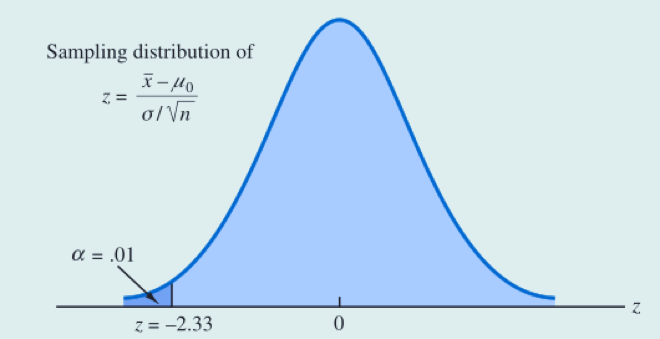
from scipy.stats import normz = norm.ppf(0.01)print(z) # -2.3263
我们发现 z = -2.33 的下侧面积等于0.01的值。根据抽样计算出的检验统计量值为 -2.67,由于小于 -2.33,得知p-值小于或等于0.01,所以我们拒绝原假设并且得出结论认为Hilltop咖啡的分量不足。
同样的,如果我们计算出来的样本统计量是大于-2.33的,这属于是更加常见的情况,也无法得出确切结论。
通常而言,使用p值法更为广泛,因为p值法提供了更多的信息,它直接告诉了我们样本均值与总体均值差异度的显著性。p值越小,差异性越大,即差异越显著。
总体均值的双侧检验
- 形式
- 原假设等于总体均值
- 备择假设不等于总体均值
- 只有这一种形式,因为等号总是出现在原假设中
- 区别
- p-值法
- 将下侧面积或上侧面积乘2即可
- 即面积对应的概率乘2,然后与显著性水平进行比较即可
- 临界值法
- 如果样本对应检验统计量的值小于等于下侧的临界值
- 或大于等于上侧的临界值
- 则拒绝原假设
- p-值法
案例应用:
Maxflight生产的高尔夫球必须达到平均驱动距离295码,才可以参与USGA的赛事。距离或大或小都是不被允许的,因此该公司需要检验其生产的高尔夫球平均驱动距离是否等于295码。
建立假设:
显著性水平:0.05
计算检验统计量:
已知生产的高尔夫球的总体标准差为12,此次抽取的样本容量为n=50,样本均值为297.6,标准误差即 ,检验统计量
。
p-值法:
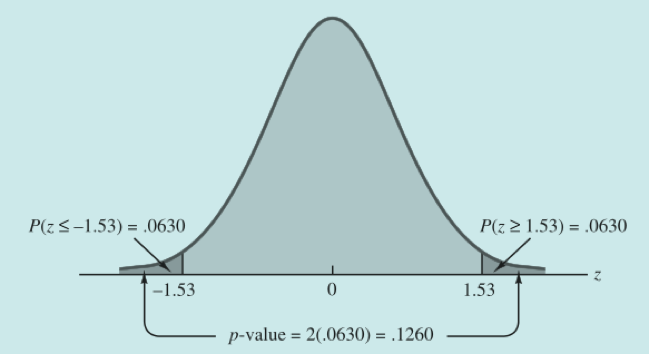
0.063 * 2 = 0.126,即p值为0.126是大于我们选取的显著性水平的,因此我们不能拒绝原假设。
临界值法:

根据临界值双侧检验的拒绝法则,我们计算出来的 , 即如果检验统计量的值小于等于-1.96或者大于等于1.96,才能拒绝原假设。而我们计算出来的z值为1.53,不满足条件,因此我们不能拒绝原假设。
双侧检验与单侧检验的一个区别在于,对应p-值法,需要将单侧的概率值乘以2,对应临界值法,我们计算的是 而非
。(
是针对单侧检验而言的)
小结

区间估计与假设检验的关系
- 结论
- 首先是有关系的
- 也可以通过区间估计来判断是否拒绝原假设
- 区间估计的置信水平与假设检验的显著性水平是互补的
- 方法
- 利用样本均值建立关于总体均值的区间估计
- 如果置信区间包含总体均值的假设值
,则不能拒绝原假设,如果没包含,则可以拒绝原假设
- 利用样本均值建立关于总体均值的区间估计
- 剖析原因
- 假设95%置信水平下建立了置信区间
- 此时对应假设检验的显著性水平为5%
- 那么
- 总体均值落在置信区间外面的概率就是5%
- 如果假设值
在置信区间外
- 那么就甘愿冒着犯第一类错误的概率拒绝原假设了
常用的p-值指导
- 准则
- p值越小,拒绝
的证据越多,进而支持
的证据越多
- 想一下那个2*2的图表
- 在得出结论拒绝原假设的情况下
- 无非两种情况,犯第一类错误或备择假设为真
- 犯第一类错误的概率即p值越小
- 则对应备择假设为真的可能性就越大
- p值越小,拒绝
- 常见的比较
- p值小于0.01
- 强有力的证据断定备择假设为真
- p值介于0.01~0.05之间
- 有力的证据断定备择假设为真
- p值介于0.05~0.1之间
- 弱的证据断定备择假设为真
- p值大于0.1
- 没有足够的证据
- p值小于0.01
均值检验(总体标准差未知)(P218)
t分布回顾
- 随着样本容量的增大(或自由度的增大),越来越接近标准正态分布
- 即使在总体数据呈偏态的情况下,t分布也有很好的拟合
- t分布概率表中直接描述的就是上侧面积,即右侧面积
- t分布的均值为0
检验统计量
- (样本均值 - 总体均值) / 样本的标准误差
- 此时样本的标准误差 = 样本的标准差 / 样本容量开根号
注意:在总体标准差未知的情况下,我们使用样本标准差来替代总体标准差,此时的变异程度更大。
一般步骤
- 建立假设
- 选定显著性水平
- 计算检验统计量(这种情况下t分布的自由度为样本容量 - 1)
t分布同样存在着单侧检验和双侧检验,基本和上面类似,这里以单侧检验进行举例:
案例应用:
某杂志对大西洋通道的机场服务进行评分,最低分为0分,最高分为10分。评分的总体均值超过7的机场将被认为提供了优质服务。选取了希思罗机场60名客人组成的一个样本,样本均值为7.25分,样本标准差为1.052分。样本数据能否表明希思罗机场提供了优质的服务?
建立假设:
显著性水平:0.05
计算检验统计量:
样本的标准误差即 ,检验统计量
。
p值法:
from scipy.stats import t# 是上侧检验,取上侧面积p_value = 1 - t.cdf(1.84, 60 - 1)print(p_value) # 0.0354
很明显,p-value小于显著性水平,因为我们可以拒绝原假设,认为希思罗机场提供了优质的服务。
临界值法:
from scipy.stats import t# 直接返回的值为负值,由于对称,取绝对值ts = abs(t.ppf(0.05, 60 - 1))print(ts) # 1.671
检验统计量的值为1.84,是大于1.671的,因为我们可以拒绝原假设,认为希思罗机场提供了优质服务。
小结
第二类错误(P224)
引入问题
- 什么情况下需要控制第二类错误,必须要得出一个决策时
- 当得出不能拒绝原假设的结论时,我们什么决策也不能做
- 进一步进行探索,我们就需要控制第二类错误
- 当同时控制第一类错误和第二类错误的可能性时
- 假设检验的结论就可以说要么是拒绝H0,要么是接受H0
案例应用
对供应商的一批电池,某名质量控制管理人员必须决定是接受这批货物,还是因为其质量差而将货物退还。假定设计规格中要求这电池的平均使用寿命至少为120小时,为了评估这批货物的质量,我们选取36节电池组成样本进行检验。
建立假设:
显著性水平:0.05
**
计算检验统计量:
已知总体标准差,则检验统计量为
根据显著性水平为0.05,也就是说上侧面积为0.025,我们可以倒推出此时的z值为1.645。根据下侧检验的拒绝法则,如果满足(下侧检验),则可以拒绝原假设。求解样本均值可知,当样本均值小于等于116.71(120 - 12 / 6 * 1.645)时,拒绝原假设。
我们想要计算第二类错误的概率,首先回忆一下什么是第二类错误,即原假设为假,却接受了原假设。在这个案例中,当电池的真值小于120小时(满足原假设为假)而我们却做出接受原假设的决定时,我们就犯了第二类错误。因此要想计算第二类错误的概率,有两个前提条件需要满足,第一:满足原假设为假(即我们选取一个假定的总体均值为112,假装实际的总体均值为112,也可以选取其它小于120的值),第二:接受原假设(即案例中的样本均值要大于116.71), 此时求解就转化为了当𝜇=112时样本均值大于116.71的概率
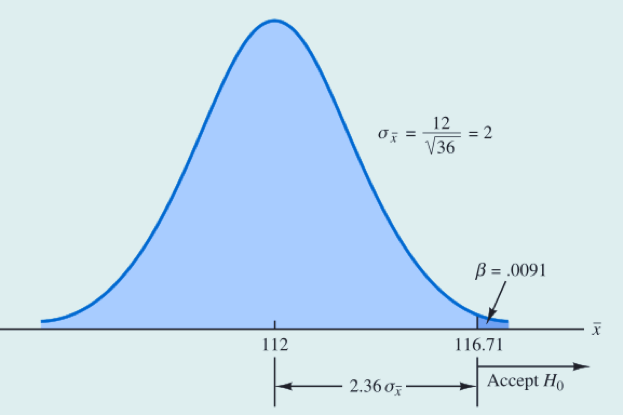
我们仔细看上面这张图,图中我们假定的总体均值为112,此时求解第二类错误的概率,就转化为了求图中阴影部分面积。(从正态分布转化为标准正态分布,还是z分数的一个应用)
由标准正态概率分布表可知,当z = 2.36时其上侧面积为1 - 0.9909 = 0.0091. 用 代表第二类错误发生的概率。我们可以得出结论,如果总体均值为112小时,则发生第二类错误的概率为0.0091。

上面这个图表示,假定不同的总体均值时,计算出第二类错误的概率。可以观察到,越接近120时,犯第二类错误的概率就越大。反之,则越小。
样本容量(P226)
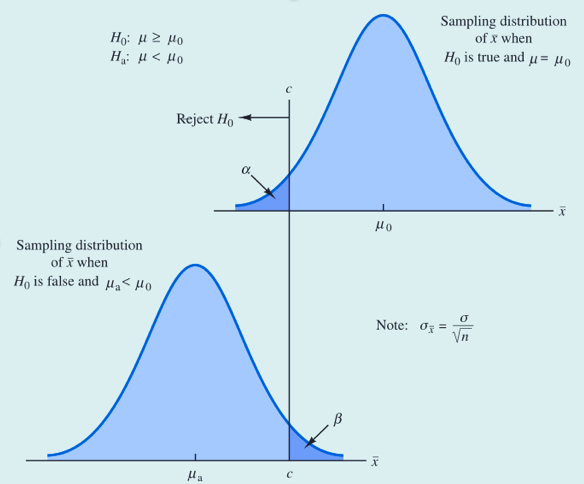
第一类错误:
当原假设为真。对于下侧检验,检验统计量的临界值记作 ,图中上半部分中垂线 c 与
相对应。如果当
时拒绝
,则发生第一类错误的概率为
。以
表示标准正态分布上侧面积为
时所对应的的 z 值,则可利用如下公式计算 c :(个人认为,可以把c理解为临界值)
第二类错误:
当备择假设为真。阴影区域的面积 恰好是当
(之间小于等于c为拒绝原假设,现在大于c为接受原假设)却接受了原假设时决策者发生第二类错误的概率。以
表示标准正态分布上侧面积为
时所对应的 z 值。可利用如下公式计算 c :
我们想要选取一个c值,使得最终得出拒绝原假设,接受备择假设的结论时,发生第一类错误的概率等于选取的值 ,发生第二类错误的概率等于选取的值
。此时我们得出接受备择假设结论时就同时控制了发生第一类错误和第二类错误发生的概率,因此上述两式所给出的 c 值是相等的。于是,如下方程一定成立:
进一步可得:
上式即为总体均值单侧假设检验的样本容量,其中 代表标准正态分布的上侧面积为
时对应的z值;
代表标准正态分布的上侧面积为
时对应的z值;
为总体的标准差;
为假设检验中样本均值的值;
为第二类错误中所采用的总体均值的值。
我们可以观察到,
,样本容量 n 之间的如下三种关系:
- 当三者中有二者已知时,即可计算得到第三者
- 对于给定的显著性水平
,增大样本容量,会导致
变大,进而上侧面积变小,即
会减小
- 对于给定的样本容量,减小
将会使
增大,相反增大
将会使
减小