第一题 海景房

GulfRealEstateProperties 有限责任公司是弗洛里达西南部的一家房地产公司。企业在广告中称自己是“地产专家”。公司对销售进行监督，搜集有关房屋地点、定价、售价和每套售出花费天数等信息，详细数据见GulfProp.csv文件。如果方位位于墨西哥湾，称之为看得见海湾的房屋，否则称之为看不见海湾的房屋。我们根据交易系统可以查看到最近售出的 40 套看得见海湾的房屋和 18 套看不见海湾的房屋的样本数据，单位以 1000 美元计。

  1. 对 40 套看得见海湾的房屋，用适当的描述性统计量对三个变量中的每个变量进行汇总。
  2. 对 18 套看不见海湾的房屋，用适当的描述性统计量对三个变量中的每个变量进行汇总。
  3. 比较你的汇总效果，讨论有助于房地产代理商了解地产市场的各种统计结果。
  4. 对看得见的海湾的房屋，求售价的总体均值以及售出花费天数的总体均值的 95%置信区间，解释你的结果。
  5. 对看不见的海湾的房屋，求售价的总体均值以及售出花费天数的总体均值的 95%置信区间，解释你的结果。
  6. 假定分公司经理要求在 40000 美元的边际误差下对看得见海湾的房屋的售价均值进行估计，在 15000 美元的边际误差下对看不见海湾的房屋的售价均值进行估计。取置信水平为 95%，则应该选取多大的样本容量。
  1. import pandas as pd
  2. df = pd.read_csv('GulfProp.csv', skiprows=1)
  3. df.head()

先看一下数据的轮廓：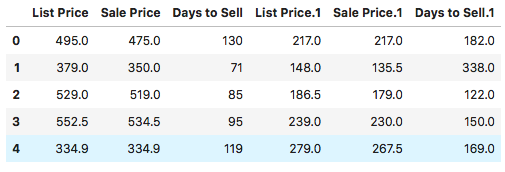
image.png
其中前面的三列为看得见海景的房子的数据 分别为定价 售价 卖出所需日期
后面三列为看不见海景的房子的数据 分别为定价 售价 卖出所需日期

第一问

  1. df[['List Price', 'Sale Price', 'Days to Sell']].describe()

执行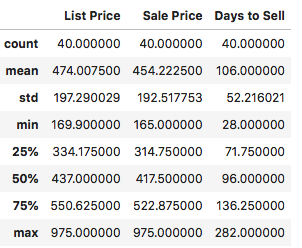
image.png
我们可以看到，位于墨西哥湾的海景房售卖中，定价最高的为97.5万美元，定价最低的为16.9万美元，中位数是在43.7万美元，和平均数47.4万美元有一定差距；卖价基本上都要比定价低；平均卖出一套海景房需要106天，最快的28天，最慢的282天，中位数是在96天。

第二问

  1. df[['List Price.1', 'Sale Price.1', 'Days to Sell.1']].iloc[:18, :].describe()

执行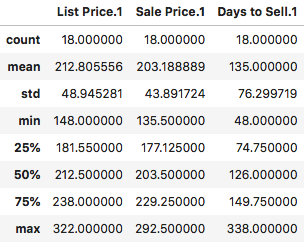
image.png
需要注意的是，针对非海景房，我们只要18套房子的样本数据。

第三问

我们可以看到，海景房售价基本是非海景房售价的两倍，甚至还不止。

第四问

  1. # 总体标准差未知，要通过t分布来计算，自由度为样本容量减去1
  3. from scipy.stats import t
  5. def confidence_interval(sample_mean, sample_size, sample_std, alpha):
  6.     # 1.计算边际误差
  7.     tv = abs(t.ppf(alpha / 2, sample_size - 1))
  8.     er = tv * sample_std / np.sqrt(sample_size)
  10.     # 2. 计算区间
  11.     upper_limit = round(sample_mean + er, 2)
  12.     lower_limit = round(sample_mean - er, 2)
  14.     return [lower_limit, upper_limit]
  16. col = 'Sale Price'
  17. sample_mean = df[col].mean()
  18. sample_size = len(df[col])
  19. sample_std = df[col].std()
  20. alpha = 0.5
  21. print(confidence_interval(sample_mean, sample_size, sample_std, alpha))
  23. col = 'Days to Sell'
  24. sample_mean = df[col].mean()
  25. sample_size = len(df[col])
  26. sample_std = df[col].std()
  27. alpha = 0.5
  28. print(confidence_interval(sample_mean, sample_size, sample_std, alpha))

执行
image.png
可以看到，针对海景房而言，售价总体均值95%置信区间为[433.5, 475.95]，售卖所需天数总体均值95%置信区间为[100.38, 111.62]。即海景房售价95%概率是在43.35万美元到47.595美元之间，海景房售卖所需天数95%概率是在100天到112天之间，如果某幢房子卖了112天还没卖出去，那售卖时间已经是落在大多数人后面了。

第五问

  1. col = 'Sale Price.1'
  2. sample_mean = df.loc[:17, [col]].mean().values[0]
  3. sample_size = len(df.loc[:17, [col]])
  4. sample_std = df.loc[:17, [col]].std().values[0]
  5. alpha = 0.5
  6. print(confidence_interval(sample_mean, sample_size, sample_std, alpha))
  8. col = 'Days to Sell.1'
  9. sample_mean = df.loc[:17, [col]].mean().values[0]
  10. sample_size = len(df.loc[:17, [col]])
  11. sample_std = df.loc[:17, [col]].std().values[0]
  12. alpha = 0.5
  13. print(confidence_interval(sample_mean, sample_size, sample_std, alpha))

执行
image.png
有两点需要注意一下：

  1. 我们调用了之前定义的confidence_interval函数。
  2. 通过loc选取元素后，结果为DataFrame类型，mean默认求每一列的平均值，求平均后为Series类型，通过values属性获取数值本身。

可以看到，针对非海景房而言，售价的总体均值95%置信区间为19.606万美元到21.032万美元之间，售卖所需天数总体均值95%置信区间为122天到148天之间。

第六问

直接参考公式 区间估计习题 - 图6 求解即可：

  1. # 我们用样本标准差s来代替总体标准差，单位为1000美元
  2. s = df['Sale Price'].std() * 1000
  3. n1 = (1.96 ** 2 * s ** 2) / (40000 ** 2)
  4. print(round(n1, 2))
  6. s = df.loc[:17, ['Sale Price.1']].std().values[0] * 1000
  7. n2 = (1.96 ** 2 * s ** 2) / (15000 ** 2)
  8. print(round(n2, 2))

执行
image.png
针对看得见海湾的房屋而言，为达到 40000 美元的边际误差，选取的样本至少应该为89个。
针对看不见海湾的房屋而言，为达到 15000 美元的边际误差，选取的样本至少应该为33个。