抽样分布(P161)
抽样
- 解决的问题
- 样本用来估计总体参数(总体特征)
- 不需要百分百准确,只需要尽可能减少误差
- 类别
- 有限总体抽样
- 简单随机抽样
- 每一个样本被等概率的抽出
- 百分之七八十都是这种方式
- 有放回抽样
- 无放回抽样
- 简单随机抽样
- 无限总体抽样
- 举例
- 正在作业的生产线,你无法知道产品的总数量
- 进入某个店铺的人流,也是源源不断
- 随机样本
- 抽取的每个个体来自同一总体
- 来餐厅吃饭的,来餐厅使用洗手间的,不是同一总体(针对服务质量问卷)
- 麦当劳使用优惠券的,不使用优惠券的,就是2个总体(针对优惠券问卷)
- 每个个体的抽取是独立的
- 如果在来吃饭的一家人中抽取了多个个体,则此时个体的抽取不满足独立
- 因为抽取的个体彼此之间应该是互不影响的
- 抽取的每个个体来自同一总体
- 举例
- 有限总体抽样
具体引用:EAI公司的抽样问题
EAI公司的人事部经理被分配一项任务,要求为公司2500名管理人员制定一份简报,内容包括管理人员的平均年薪和是否已完成公司管理培训计划的管理人员所占的比率。2500名管理人员构成此项研究的总体。现在,假设我们无法从公司的数据库中获得全部EAI管理人员的必要信息。那么我们能否不用总体的2500份数据,而是用一个样本,从而获取对这些总体参数的估计呢? 假设样本的大小为30,我们现在从这30名管理人员的样本入手,探究利用样本研究EAI问题的可能性。
我们先熟悉一下数据:
df = pd.read_csv('EAI.csv')df.head()
执行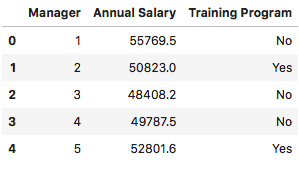
print(len(df)) # 2500print(df['Annual Salary'].mean()) # 51800print(df['Annual Salary'].std()) # 4000print((df['Training Program'] == 'Yes').sum() / len(df)) # 0.6
经过计算,我们知道这2500名管理人员的总体均值为51800美元,总体标准差为4000美元,完成培训计划的总体比率为0.6,这些都属于总体的参数。
点估计
- 样本统计量
- 相应的样本特征
- 比如样本的平均数,样本的标准差
- 比如样本的比率
- 满足某个条件的样本数 / 样本总数
- 点估计量
- 即相对应的样本统计量(比如总体均值的点估计量就是样本均值)
- 很明显,点估计量和总体参数是有误差的
- 且误差是可预期的
- 即落在某个区间的概率大小
- 应用建议
- 使用样本去推断总体时,抽样总体与目标总体应该是高度一致的
- 即满足上面随机样本的两个条件
看一下我们抽到的30名管理人员的样本数据: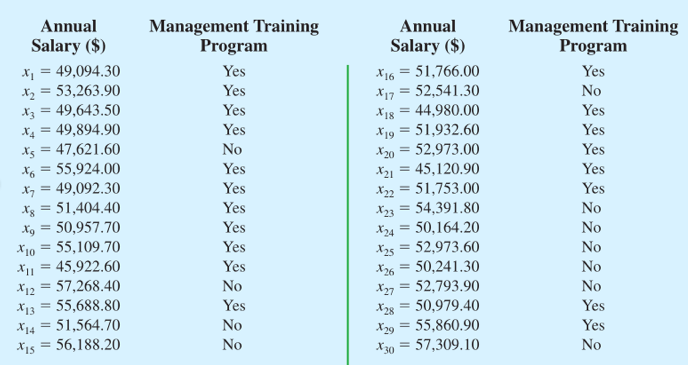
进一步的,我们计算出这个样本中薪资的平均数为51814美元,标准差为3348美元。
(标准差的计算方式,就是我们在描述统计学部分介绍过的,离差平方和/(样本容量减一),将结果开根号)
点估计性质
- 概念
- 在将一个样本统计量作为点估计量之前
- 我们需要检查一下三个性质
- 如果满足,则是好的点估计量
- 性质
- 无偏性
- 举例:样本均值的期望要等于总体期望
- 有效性
- 多个点估计量选标准误差较小的
- 比如一个样本容量为30的点估计量和一个样本容量为50的点估计量
- 一致性
- 随着样本容量的扩大,点估计量的值应该越来越靠近总体参数
- 无偏性
抽样分布
将抽取一个简单随机样本的过程看作一个试验;那么样本的均值 就是对试验结果的一个数值描述;从而样本均值
是一个随机变量,它会拥有均值或数学期望、标准差和概率分布;而该随机变量的概率分布就称为是样本均值的抽样分布。
- 概念
- 多次进行简单随机抽样,得到不同的简单随机样本
- 每个样本平均数的取值存在各种可能
- 我们称样本平均数的概率分布为样本平均数的抽样分布
- 本质上抽样分布是概率分布
- 统计量抽样分布
- 任何特定样本统计量的概率分布称为该统计量的抽样分布
- 比如平均数,比率,方差等
- 可以对比上面平均数抽样分布的概念
- 均值的抽样分布(样本平均数)
- 数学期望
- 公式
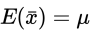
- 解释
- 均值的数学期望(均值的均值)
- 总体均值
- 公式
- 标准差
- 公式
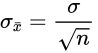
- 解释
- 总体标准差
- 样本容量
- 公式
- 标准误差
- 点估计量的标准差
- 比如上面样本平均数的标准差就可以称为均值的标准误差
- 有助于确定样本均值与总体均值的偏离程度
- 分布形式
- 总体服从正态分布
- 任何样本容量下,均值的抽样分布都是正态分布
- 总体不服从正态分布
- 衍生出了中心极限定理
- 统计学家表明
- 当样本容量大于或等于30时,均值的抽样分布近似正态分布
- 当总体出现严重偏态或异常值时,可能需要容量达到50
- 注意,这只是个基准值,实际可能还要比这大一些
- 当样本容量足够大时
- 均值的抽样分布近似正态分布
- 衍生出了中心极限定理
- 总体服从正态分布
- 应用
- 问题
- 我们为什么会对均值的抽样分布感兴趣?
- 其实是为了根据均值的期望来估计总体的期望
- 求解出一个概率值信息
- 步骤
- 转化为正态分布
- 通过z-score转为标准正态分布
- (减去均值) / (标准差)
- 求解概率
- 均值的抽样分布与样本容量的关系
- 考虑一下标准误差的公式
- 总体标准差是不变的
- 样本容量越大,均值的标准误差越小,正态分布的曲线越陡峭,落在某一个特定范围的概率越大
- 换句话说,样本容量越大,我们估计总体的均值就越真实
- 问题
- 数学期望
具体应用:
我们对选取30名管理人员组成一个简单随机样本的过程不断重复,假设重复了500次,(通常意义上,我们指的是无放回抽样)我们就会得到500个这样的简单随机样本所计算的平均值与标准差等数据。表中给出的是500个 的频数及频率分布。
500个简单随机样本的 和
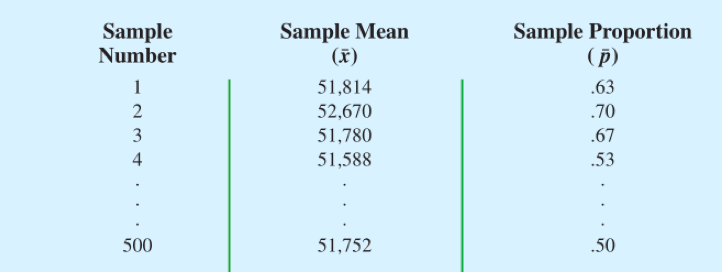
500个简单随机样本的频数与相对频率
绘制出样本均值概率分布的直方图:(注意这个地方连续型变量转化为离散型变量了,中心位置靠近51800美元)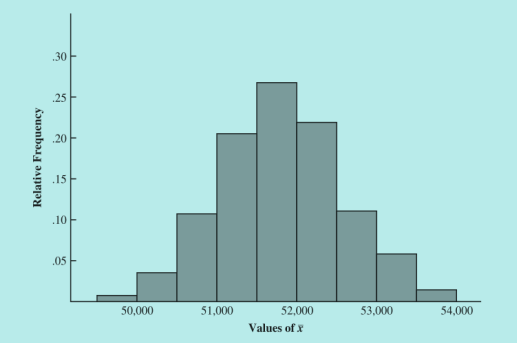
绘制出样本比率对应的直方图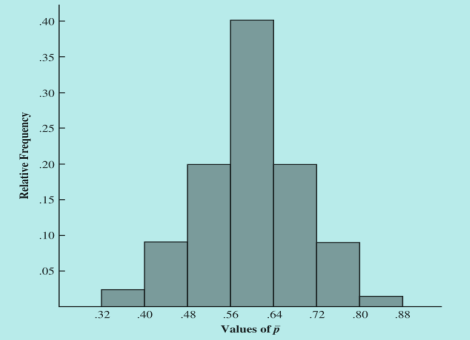
想特别说明一下:为什么我们需要绘制出直方图?因为通过直方图,我们可以看出数据的分布,是均匀分布,是左偏,是右偏,还是钟型分布?确定了分布形态之后,有利于我们确定抽样的样本容量是否合适,是否可以模拟正态分布,因为当抽样总体不符合正态分布时,或严重偏态时,我们需要尽可能扩大抽样的样本容量。
看一下样本容量与抽样分布形态的关系,随着抽样样本容量越来越大,抽样分布呈正态分布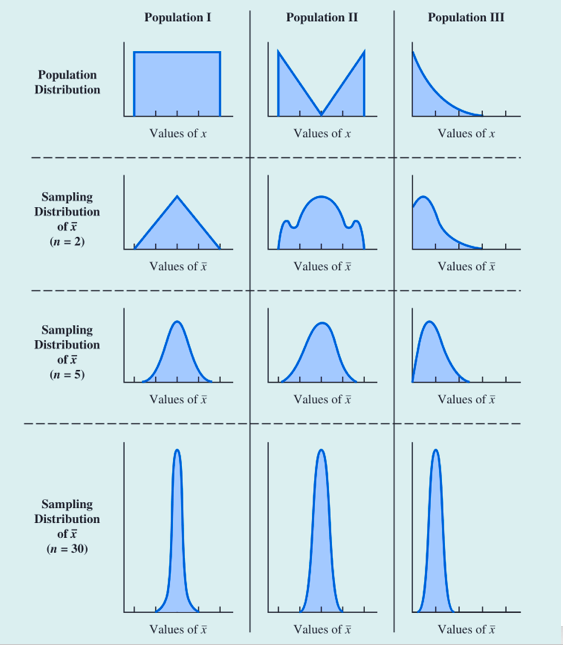
特别思考
不同的简单随机样本得出的样本均值是不同的,我们关心的是由大量简单随机样本产生的均值的所有可能值的均值。(均值的均值,针对这个例子而言,就是500个均值的均值),根据上面的公式,对于简单随机抽样,样本均值的数学期望就等于我们抽取简单随机样本时总体的均值。我们拿到原始数据文件通过下面的代码来模拟一下。
df = pd.read_csv('EAI.csv')num = 30 # 30个管理人员组成一次随机抽样样本count = 500 # 进行500次随机抽样试验salary = 0for i in range(count):salary += df.sample(num)['Annual Salary'].mean()print(salary / count)
上面代码块运行3次的结果依次是51753.56481333334,51835.55512666663,51802.68038666673 尝试着设置count为10000次,计算结果依旧不是刚好等于51800(总体的年薪均值为51800美元),根据公式,EAI研究中样本均值所有可能值的均值也等于51800美元,至于这个地方计算结果为啥不等于51800,我理解是,我们并没有取到样本均值所有的可能值,也没办法完全获取到,因为抽样的次数可以无限多,样本的容量也可以发生改变,只能是通过数学知识来证明这个公式。
从网上看到一种证明方式:
因为抽样的样本均值 的分布形态与总体
的分布形态是同分布的,所以:
案例应用
为了强调样本均值标准差与总体标准差的区别,我们称样本均值的标准差为均值的标准误差(standard error)。
一般地,标准误差指的是点估计量的标准差。
我们500次抽样分布的标准误差如下:
回到EAI问题,人事部经理关心的问题如下:根据30名管理人员组成的简单随机样本,得到的样本均值在总体均值附近±500美元以内的概率有多大?
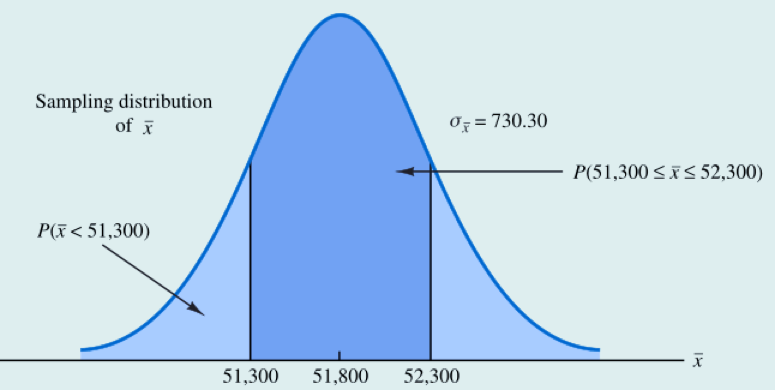
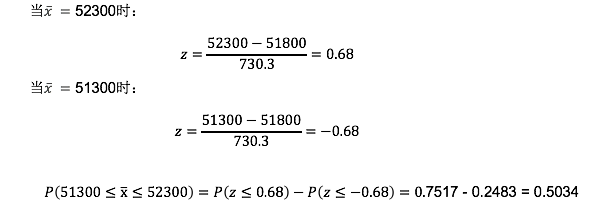
我们想要计算概率,第一个想到的就是标准正态分布,任何一个正态分布都可以通过z分数转为标准正态分布。可以参考教材(P173, P152, P66)z值是以x的标准差为度量单位的正态随机变量x与其均值之间的距离(z值表示的是距离;表示随机变量x和总体均值间的距离;该距离以x的标准差为度量单位)。其实,样本统计量和z值之间是有一个对应关系的,转化后的z值分布就是一个近似(可视为)均值为0,标准差为1的标准正态分布。在一个具体的案例中,通过样本统计量可以推出z值,反过来,通过z值也可以倒退出样本统计量。
样本容量与 抽样分布的关系举例:
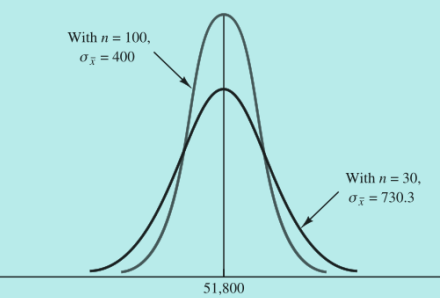
很明显,随着样本容量变大,落在某一特定范围内的概率会变大,从我们上面的公式也可以看出来。
区间估计(P184)
引言
- 我们知道点估计量无法给出总体参数的一个准确值
- 因此衍生出了区间估计
- 对比
- 点估计估计的是一个具体总体参数的大小,即一个点
- 而区间估计估计的是围绕点估计量的一个区间,更加准确
- 联系
- 区间估计的一般形式
- 点估计 +- 边际误差
- 这里的点估计指的是在某一个样本容量下,计算出来的一个具体的点估计值
- 区间估计的一般形式
- 边际误差
- 衡量样本得出的点估计量与总体参数的接近程度
- 目的
- 区间估计的目的在于,提供基于样本得出的点估计与总体参数值的接近程度方面的信息
总体标准差已知
- 问题
- 由样本均值来估计总体均值?
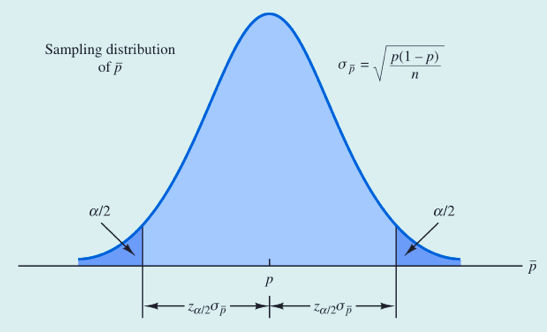
- 置信水平
- 通常指多大可能,多大把握
- 其实本质上是概率大小
- 常用的
- 90%的置信水平
- 此时的阴影部分面积为90%,对应的a值为1-90%为10%;
- 对应的上侧面积为10% / 2 = 5%
- 即整个的左侧阴影面积占比为95%,此时对应的z值为1.645
- 95%
- 0.975
- 1.96
- 99%
- 0.995
- 2.576
- 90%的置信水平
- 置信系数
- 置信水平的小数形式
- 比如0.95,0.99等
- 注意
- 置信水平越高,a值越小,统计量z值越大,边际误差越大,置信区间的宽度也越大
- 通常指多大可能,多大把握
- 边际误差计算
- 前提:在某一个置信水平下
- 比如95%水平下,边际误差 = 1.96个标准差
- 公式
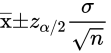
- 解释
- 1-a为置信系数
- 上侧面积为a/2时对应的z值
- 公式的后面一部分
称为是边际误差
- 边际误差就等于
乘以样本的标准误差
- 想象一下这个公式为什么这么写
- 想一下标准正态分布的曲线
- 1-a为置信水平,代表概率,即概率密度函数下方的面积
- 左右是对称的,围绕在总体均值周围
- 因此上侧的面积:1/2 - (1-a)/2 = a/2
- 计算出来的z值就是相对于均值u,标准差的个数
- 最后乘以标准差的值大小,因为通常来说我们的抽样分布是符合正态分布,而非标准正态分布的(标准正态分布标准差为1)
- 通过累计概率比对标准正态概率表时,是通过1-a/2去比对的
- 解释
案例理解:
Lloyd百货公司每周选取100名顾客组成一个简单随机样本,目的在于了解他们每次购物的消费额,令 x 表示每次购买的消费额,样本均值是Lloyd全体顾客每次购物消费额的总体均值 𝜇 的点估计。Lloyd公司的这项周度调查已经进行了很多年。根据历史数据,假定总体标准差已知,为 𝜎 = 20 美元,并且历史数据还显示总体服从正态分布。
最近抽样的100名顾客,得到的样本均值为82美元,样本的标准误差为2美元。(总体标准差/样本容量开根号)
那么问题来了?我们想要基于最近抽样的100名顾客,推断出总体均值的一个范围,要求落在这个范围内的概率为95%。
查标准正态表后我们发现,任何正态分布随机变量都有95%的值在均值附近正负1.96个标准差以内。因此当均值的分布为抽样分布时,一定有95%的值落在下面的阴影区域。也就是说,在样本容量为100的情况下,样本均值的所有值中有95%落在总体均值u附近正负3.92(1.96 * 2)以内。
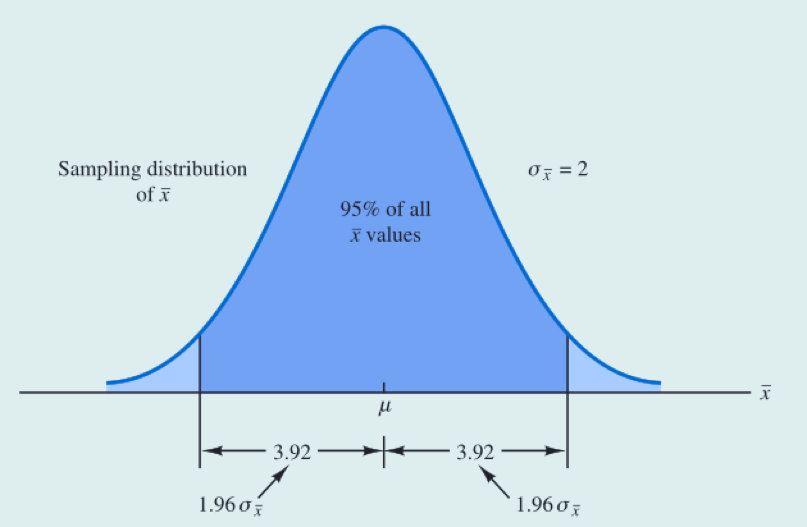
在95%的把握下,我们得出样本均值与总体均值的关系如下所示:
进一步可得:(注意,这是95%置信水平下的计算)
为了更加深刻的理解样本均值与总体均值间的关系,我们放上一张课本上的截图:
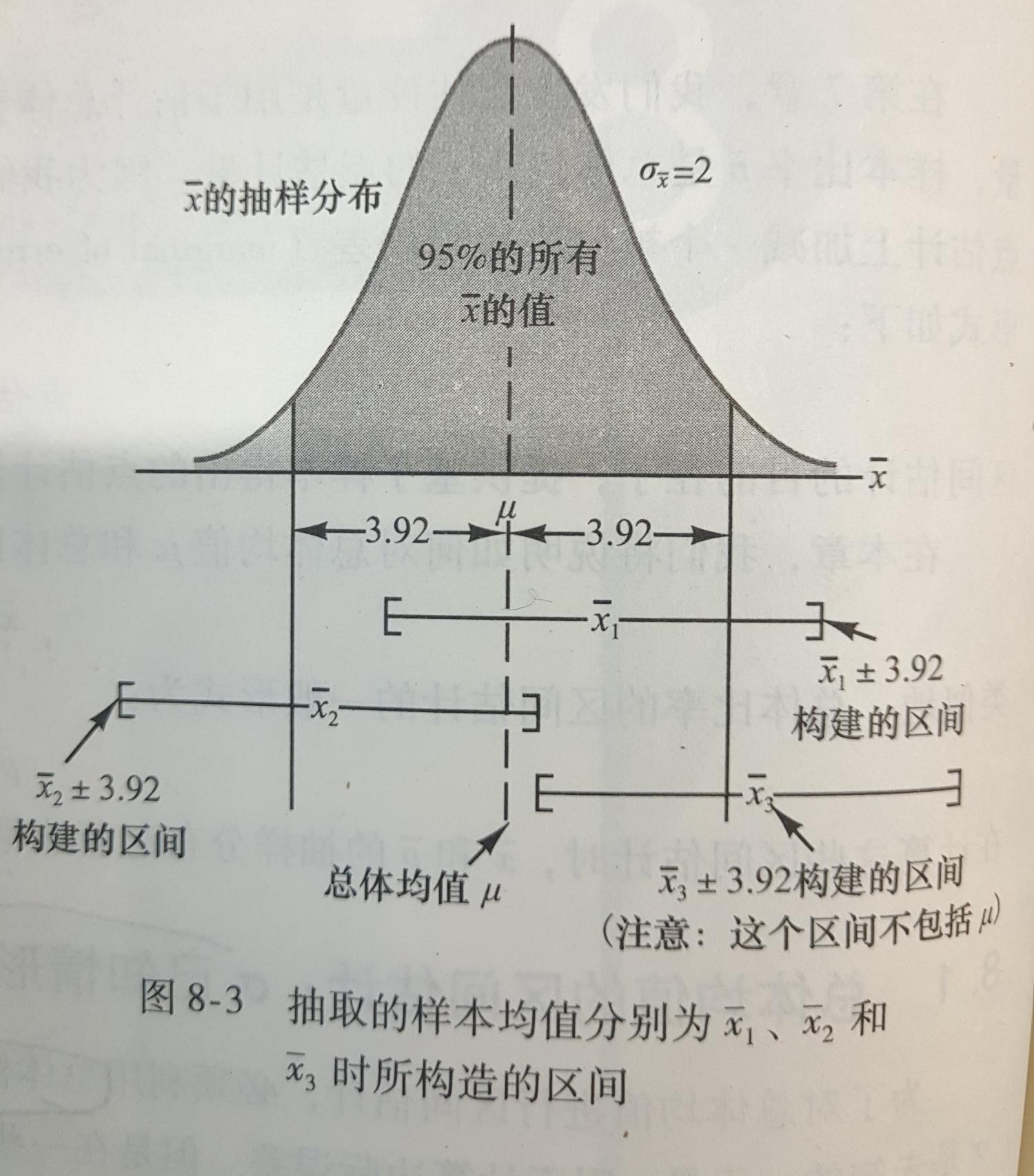
上面这个图简单展示了3个样本均值正负3.92的情况,注意第三个样本构造的区间是不包括总体均值的。因此,我们得出结论,在样本均值加减3.92构造的所有区间中有95%包括总体均值,所以我们说有95%的把握相信区间[78.08, 85.92]包括总体均值u。我们称这个区间是在95%的置信水平下建立的,其中数值0.95称为置信系数,区间[78.08, 85.92]称为95%置信区间。
回到我们的原始问题上来,依据当前的样本数据,估计总体均值所在的95%置信区间是在什么范围呢?

我们可以看到,样本容量越大,边际误差(总体标准差 / 样本容量开根号)越小;
置信区间是依赖于样本的,样本发生了变化,均值变了边际误差也变了,进而置信区间也会发生变化。
代码求解:
import numpy as np
from scipy.stats import norm
def confidence_interval (sample_mean, sample_size, population_std, confidence):
alpha = 1 - confidence
# 根据概率求解z值 它的逆操作是norm.cdf(z_score),根据z值求概率,即阴影面积的大小
z = abs(norm.ppf(alpha / 2))
upper_limit = sample_mean + z * population_std / np.sqrt(sample_size)
lower_limit = sample_mean - z * population_std / np.sqrt(sample_size)
return [lower_limit, upper_limit]
print(confidence_interval(82, 100, 20, 0.95))
对上面的代码求解时加绝对值abs解释一下,通过概率求解z值,求解出来的是负值,这一点要特别注意。
对数值含义的一点理解:
我们来好好理解一下,它表示上侧面积为
时对应的数值,准确来说是这样的,上侧面积占
,下侧面积占
,中间阴影面积占
,总的加起来是概率值1;因为在标准正态分布的概率密度函数中,均值为0,所以此时计算出来的
,正好是使得样本均值加减
个标准差所构造的区间满足要求。而在总体标准差已知的情况下,样本标准差的公式就是
,理清了这其中的关系后,会感觉一切都是那么水到渠成。
总体标准差未知
- 引言
- 更加普适的情况
- 因为大多数情况下,我们是不知道总体标准差的
- t分布
- 定义
- 小样本
- 强假设:总体服从正态分布
- 总体标准差未知
- 延伸
- 即便总体是偏态的
- 当样本容量足够大时,t分布也有很好的效果
- 性质
- t分布的均值为0
- (P191) 自由度 = 样本容量 - 1
- 独立信息的个数
- 随着自由度的增大,t分布与标准正态分布之间的差别越来越小,由此可大致想象出t分布的曲线
- 定义
- 公式
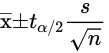
- 解释
- s为样本标准差
- 1-a为置信系数
- 注意这里的t分布自由度为n-1
- 下标表示上侧的面积为a/2
- 解释
放几张t分布的图,关于t分布的轮廓,我们是要有印象的:
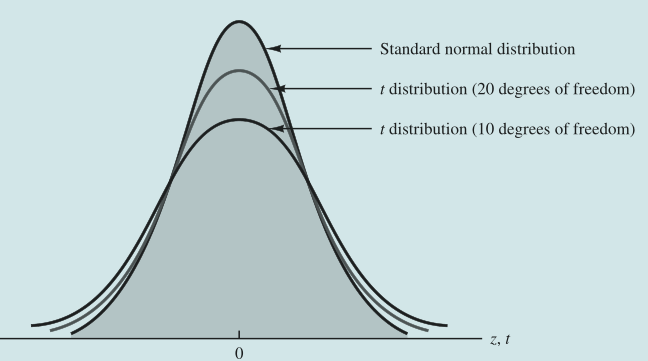
注意:在自由度无穷大时,t分布是接近于标准正态分布的。
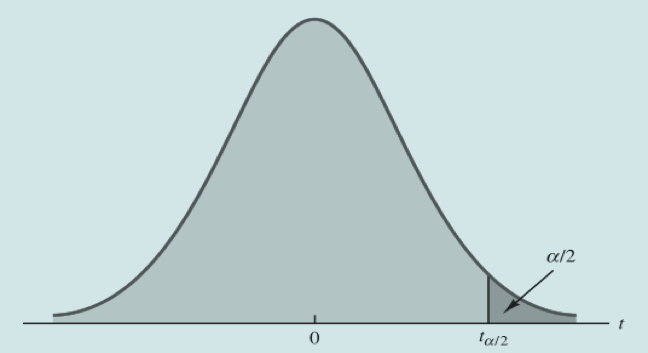
同样的,求解上侧面积为 时对应的
,所谓上侧面积就是x轴正方向,下侧面积就是x轴负方向。
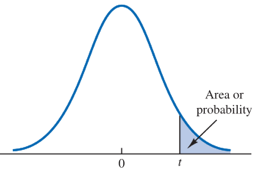
代码实现:
import numpy as np
from scipy.stats import t
def confidence_interval(sample_mean, sample_size, sample_std, confidence):
alpha = 1 - confidence
# 根据概率求解t值,或者是求解阴影面积,它的逆操作是t.cdf(t_score)
tv = abs(t.ppf(alpha / 2, sample_size - 1))
upper_limit = sample_mean + tv * sample_std / np.sqrt(sample_size)
lower_limit = sample_mean - tv * sample_std / np.sqrt(sample_size)
return [lower_limit, upper_limit]
print(confidence_interval(9312, 70, 4007, 0.95))
在大多数情况下,我们是没办法知道总体标准差的,所以在实际应用中,t分布使用的还是很广泛的。
案例理解:
已知样本中70个家庭的信用卡余额数据,我们计算出样本均值为9312美元,求总体均值的95%置信区间。
对于95%的置信区间,置信系数1-α=0.95,于是α=0.05。自由度为70-1=69,对应的t=1.995。同时计算出样本标准差为4007美元,于是得到置信区间估计:,进一步可得置信区间为
。
样本容量
- 抛出问题?
- 虽然统计学家根据经验说抽样30个50个就近似正态分布
- 可是当总体为几百万,几千万呢?那显然不是30个50个
- 推演过程
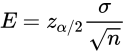
- 令E代表希望达到的边际误差
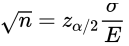
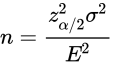
- 应用
- 通常情况下,会根据业务需要给出边际误差
- 进而根据公式求出需要抽样的样本容量
我们进行区间估计的大前提是总体数据服从正态分布,如果总体的分布形态是偏态的,那么根据中心极限定理,只有抽取的样本容量足够大,才可以近似正态分布。而通过边际误差来确定样本容量,就是为了确保样本容量足够大。比如上面信用卡的例子,假设我们想要边际误差在1000美元以内,直接代入公式进行求解即可。
注意一点:通过这种方式来确定抽样的样本容量时,要求总体标准差是已知的。(这公式和t分布没关系)
如果总体标准差是未知的,我们使用以下方法给出
的初始值或计划值,仍可以使用上述公式。
- 根据以前研究中的数据计算总体标准差的估计值作为
的计划值
- 利用实验性研究,选取一个初始样本,以初始样本的标准差作为
的计划值
- 对
进行判断或最优猜测。例如找出总体的最大值最小值,将极差除以4作为标准差
的粗略估计
总体比率
- 概念
- 当np>=5并且n(1-p)>=5,样本比率的抽样分布可近似服从正态分布
- 公式
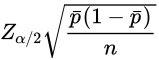
总体比率的估计同上面总体均值的估计是类似的:
值得说明的一点是:在计算样本的标准差时,我们使用样本比率来估算总体比率。
总体比率的区间估计如下所示:

