微积分的三个中心思想:微分,积分,两者互逆
Hard Problem => Sum of many samll values
将复杂问题分割成一个个小问题求解,从近似到精确的思想
我们知道, π 的定义为圆的周长除以直径
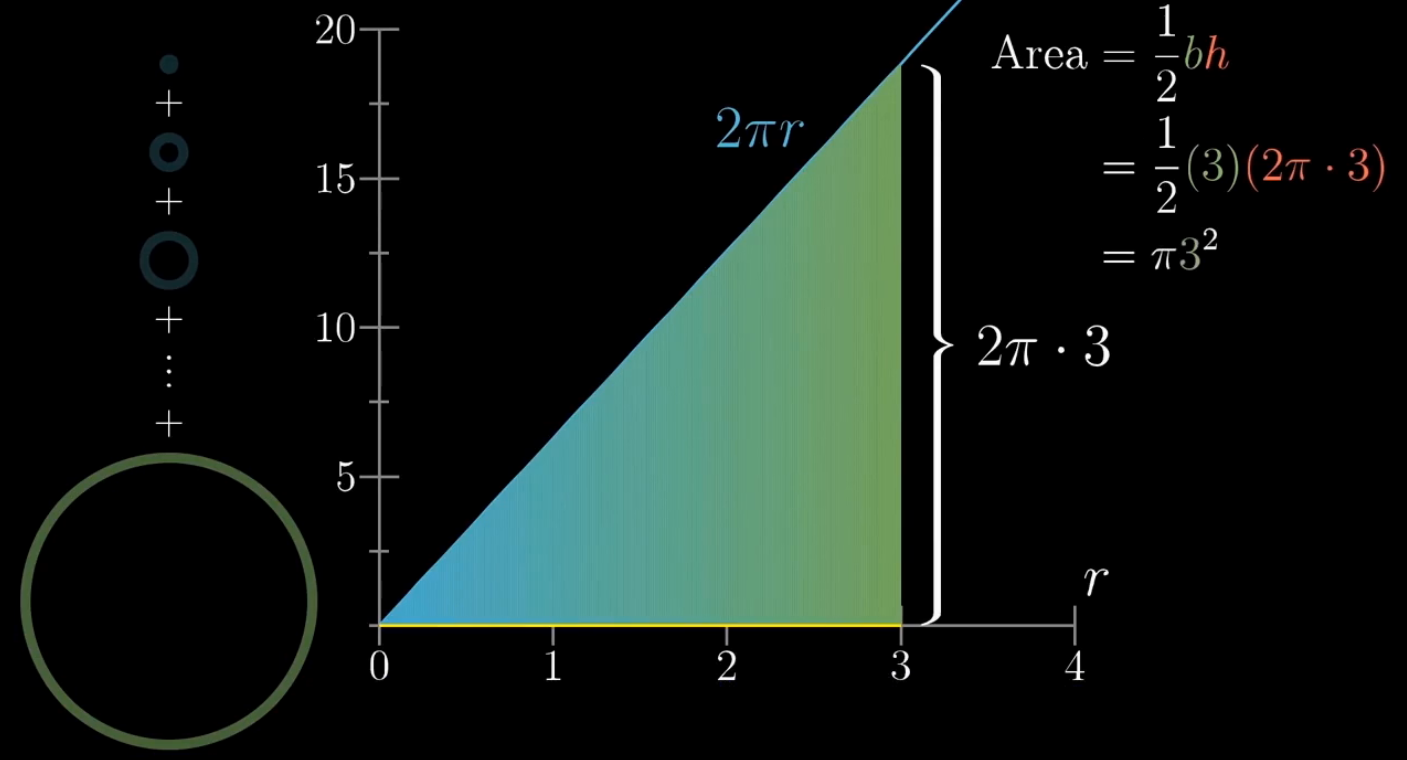
那我们考虑一个问题,怎么来论证一下圆的面积为 π r 呢?
- 下图中左边每一个同心圆的面积都可以等同于右侧直线下方长方形的面积(同心圆剪开之后,长度为2 π r,宽度为dr)
- 当dr足够小时,就可以近似成三角形的面积来求解

注意图中y轴的刻度相对于x轴的刻度作了压缩处理
- 其中A(x)是表示曲线下方面积的函数
- dA 表示图中黄色阴影部分的面积
- dx 表示长方形的宽度
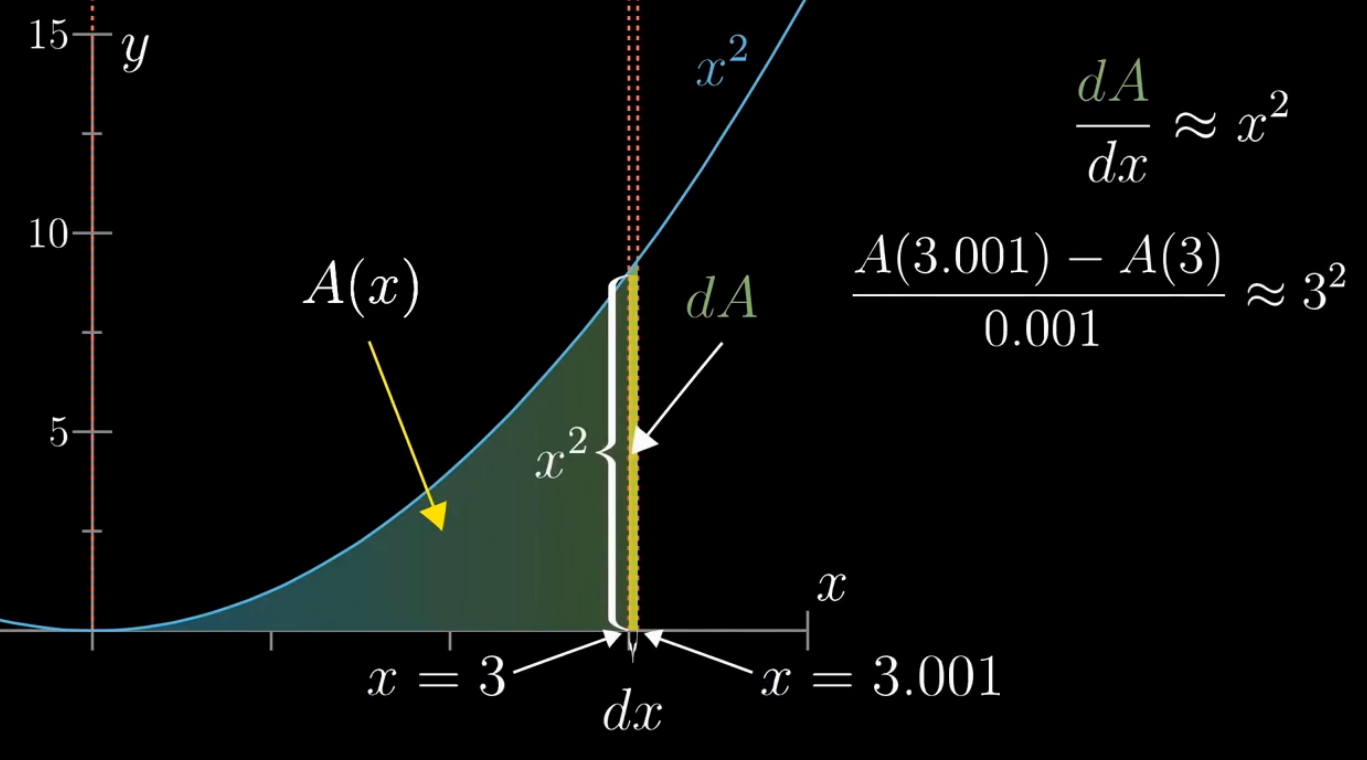
从长方形面积的角度来讲,dA 确实是等于 dx * x,约等于该点的高度
导数就是当dx越来越小趋近于0时,上图中比值的结果。
导数的悖论
汽车行驶问题
计算汽车行驶的速度是需要距离变化量除以时间变化量的,那汽车仪表盘上显示的速度是怎么计算出来的?

速度的直观表示为曲线上某一点的斜率
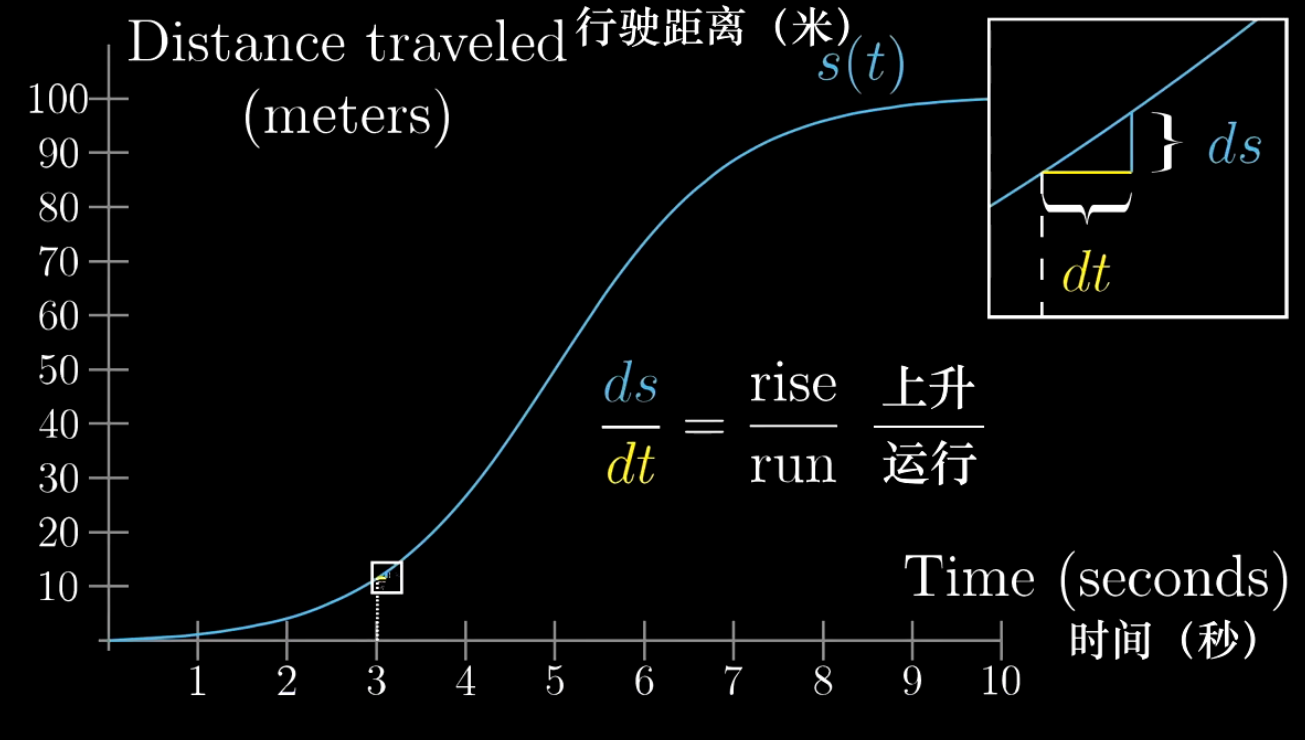
认识导数
针对上图中的dt,它是有实际大小的,无限趋近于0,但不等于0;
导数的含义是表示某个点附近的变化率,而不是瞬时变化率;(瞬时的变化是没有意义的,变化总是要有对比的)
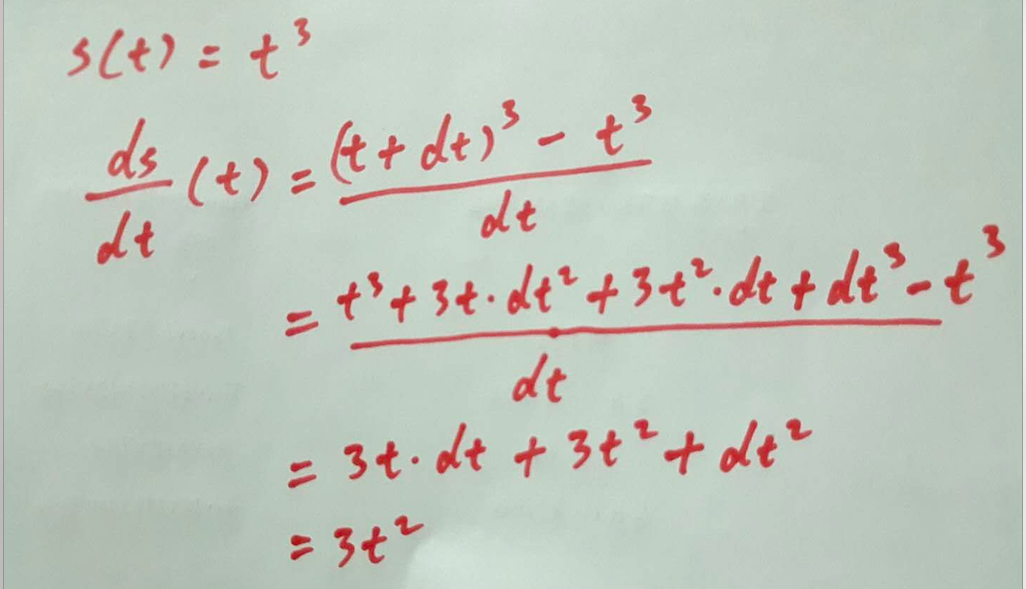
当dt无限趋近于0时,含有dt的项可以忽略不计(等号左侧还有一个dt,其实是微小变化量的平方)。
当 t = 2时,值为12,表示曲线上该点的斜率为12;即 t = 2时,汽车的行驶速度为每秒12米。
矛盾
我们考虑一个问题,当t = 0秒时,汽车有没有在移动?如果没有那汽车又是什么时候开始移动的?
根据我们前面计算出来的导数方程,t = 0 代入结果为0,如果说没在移动,那我们就犯了一个错误。
单纯研究某一时间点(瞬时)的速度是没有意义的,这里t = 0也是一样。我们只能说t = 0附近的速度变化率近似于0,0是该点附近速度的一个很好的度量。
用几何来求导
导数的实质是要看某个量的微小变化与它所导致的另一个量的微小变化有什么关系?
微小变化量才是导数的本质
幂函数求导
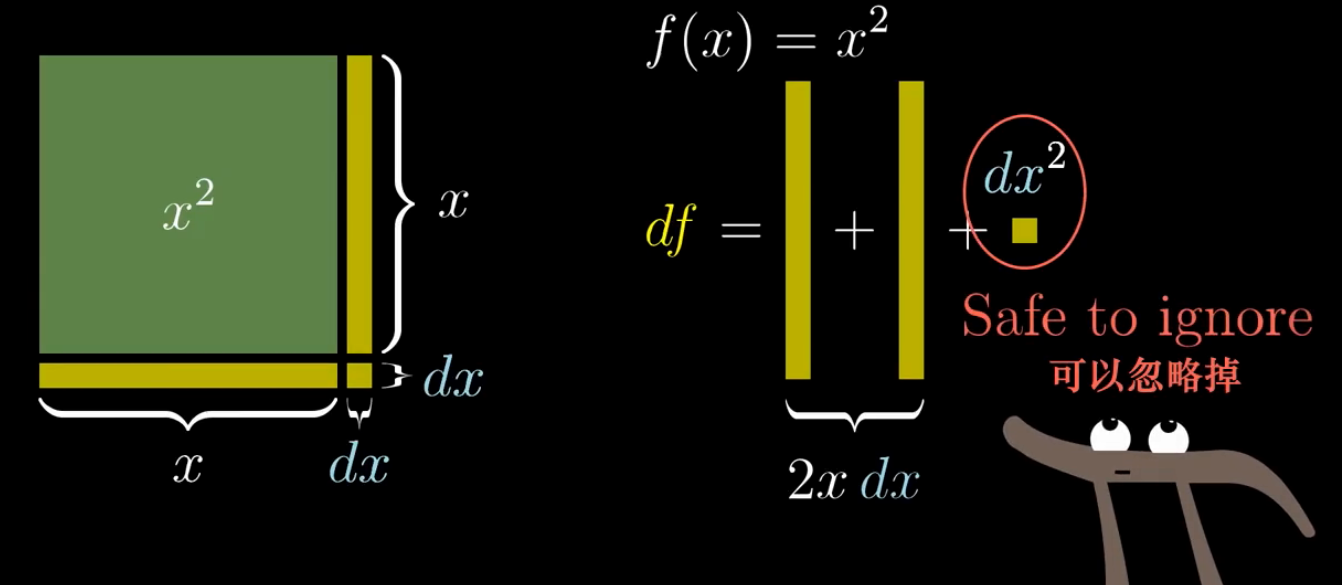
dx是一个微小的值,任何多于一个dx的项都可以被忽略。(即微小变化量的平方可以被安全的忽略)
把图中等号右侧的dx移到左边,不就是求导的结果么
当x=3时,每增加一单位长度引起的面积变化率就会是2*3=6,它是有实际意义的。
对于x的立方,可以想象成是立方体

x的n次方相减之后,就没有了
dx的平方可以忽略掉
等号右侧的dx移到左侧,幂函数的求导结果就为 nx
三角函数求导
想对导数有一个更准确的认识,就需要看函数的真实含义,而不是看函数的图像。
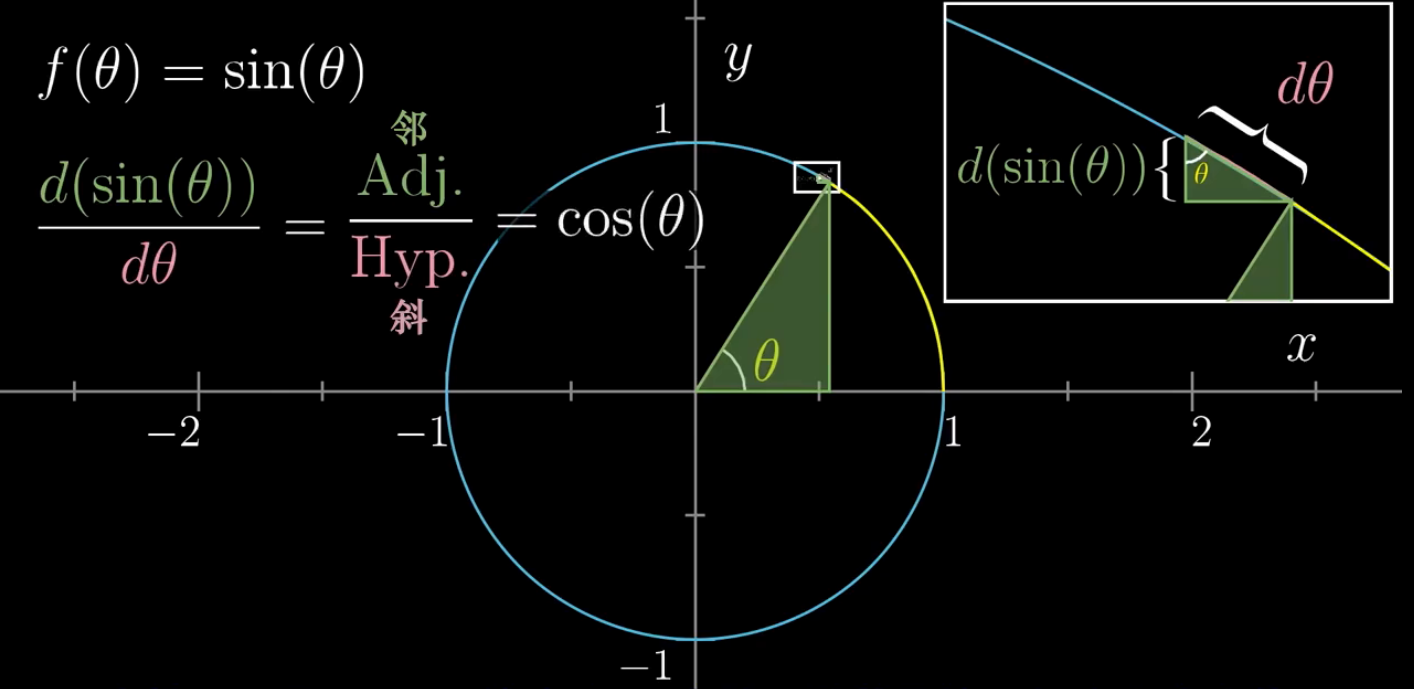
y值的微小变化量 / x值的微小变化量 = 导数的结果
同样的思路,我们可以计算出余弦函数 cos 的导数就为 -sin
这里需要注意之所以包含负号,是因为随着自变量的增加,因变量的值是在变小的。因此y的微小变化量也就是负的了。
直观理解链式法则和乘积法则
加法法则
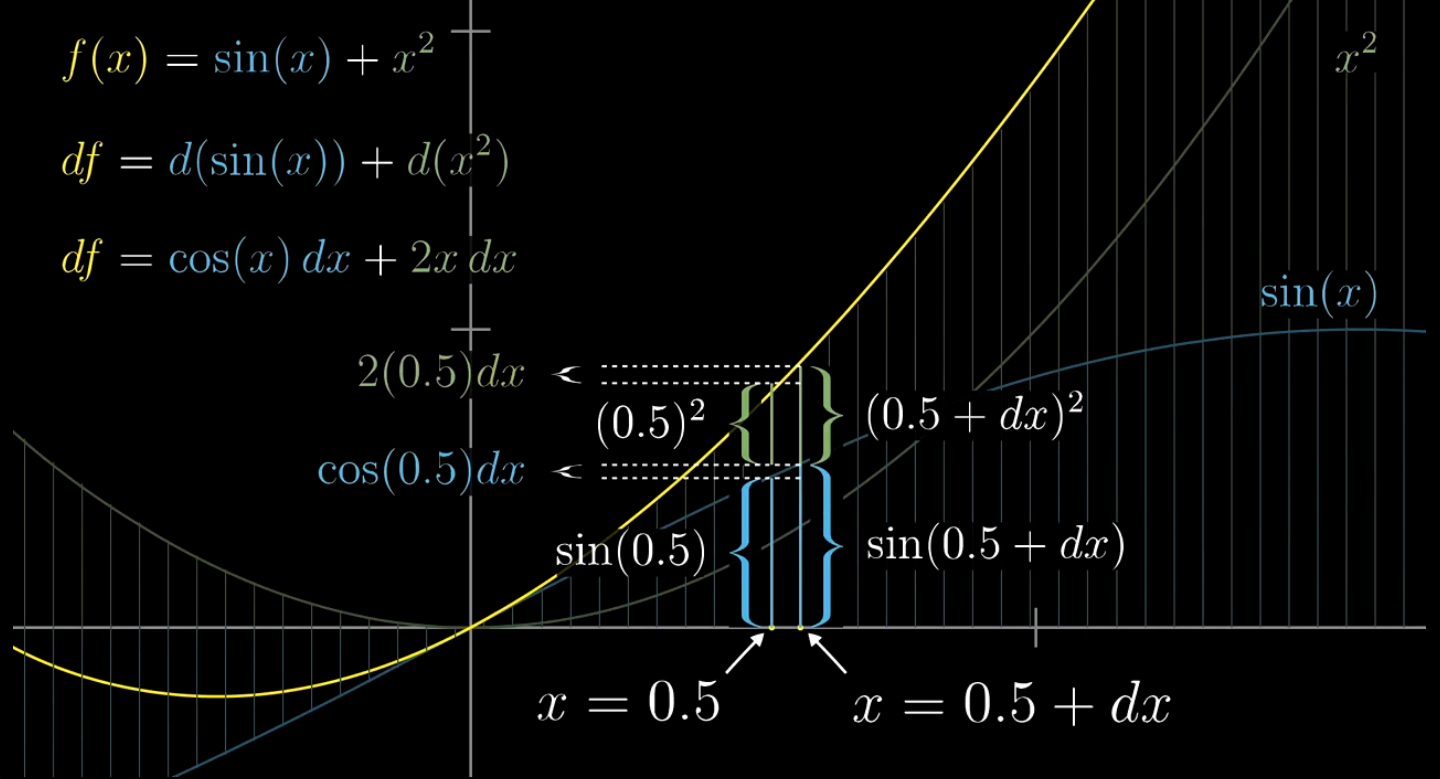
dx移动等号的左侧,即是求导的结果。
多个函数和的导数 = 每个函数导数的和

乘法法则
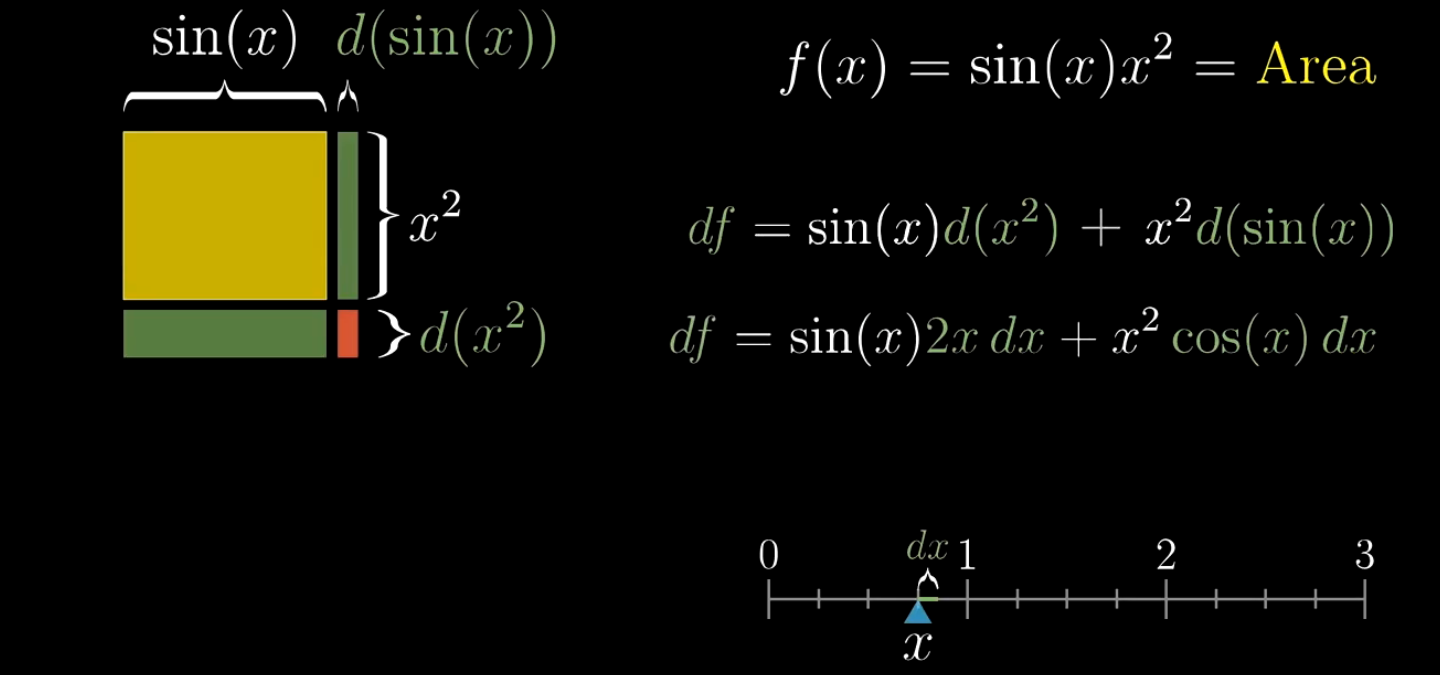
图中 df 就是当 x 添加微小变化量 dx 时,矩形新增的面积。包括两块绿色区域和一块红色区域。
其中红色区域为 d(x) * d(sin(x)),其中每个因子都会产生一个dx,结果就是 dx平方 的倍数(微小变化量的平方),可以被安全忽略。

链式法则
链式法则的应用对象主要是复合函数
复合函数求导就像剥洋葱一样,需要一层一层剥开它的心,有时还会泪流满面。
我们以复合函数 y = sin(x) 为例进行解释
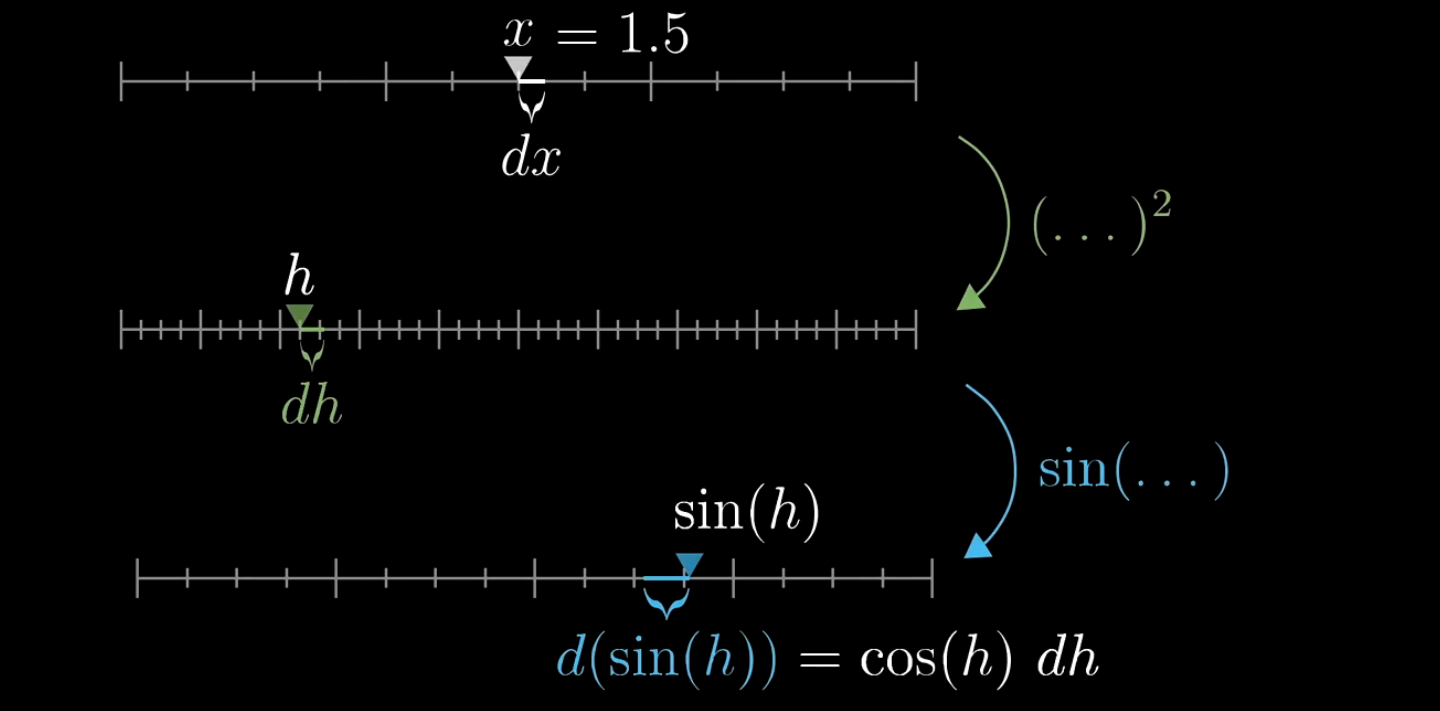
当轴1上自变量 x 新增变化量 dx 时,
此时轴2(表示 x)新增变化量 d(x),为了方便起见,我们令 h = x,即轴2上新增变化量 dh,
此时轴3(表示正弦函数 sin(x))新增变化量 d(sin(x)),即 d(sin(h)),进行计算即 cos(h) d(h),再计算即 cos(x) 2x * dx

先对外层函数求导,再对内层函数求导,结果相乘。
注意:在对外层函数求导的时候,内层函数被视为是一个整体。(想象上面例子中的h)
上图中外层求导的分母 dh 和内层求导的分子 dh 是可以约掉的,最终结果就是 dg / dx,即复合函数整体对自变量x进行求导。
指数函数求导
重要性质
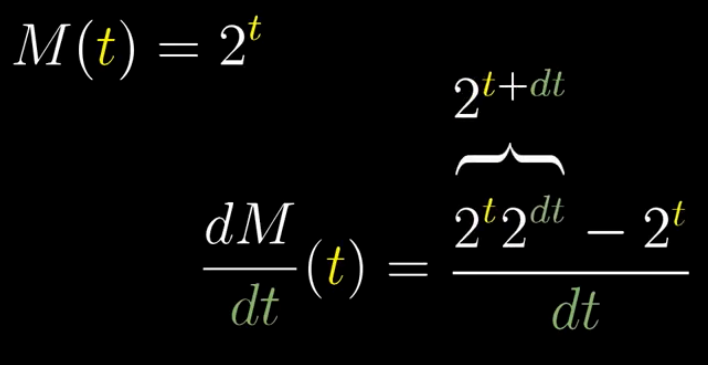
指数上的加法可以拆分成乘积的形式
谜之常数
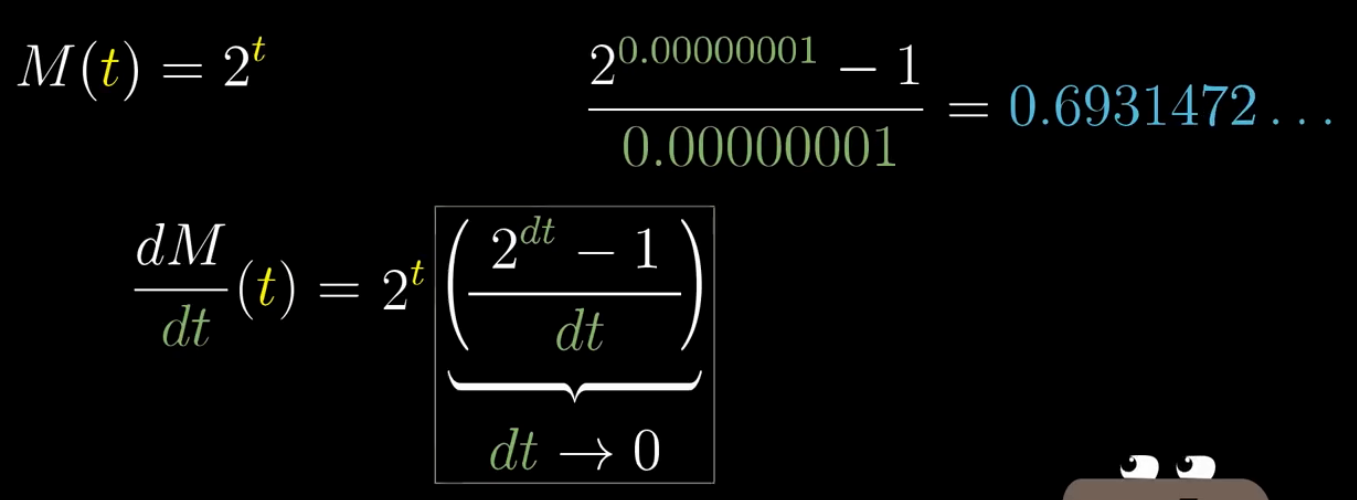
随着 dt 取值越来越小,图中方框部分的结果越来越接近0.6931。
我们可以感受到指数函数的导数就是它本身和一个常数的乘积。
那这个常数是固定的吗?
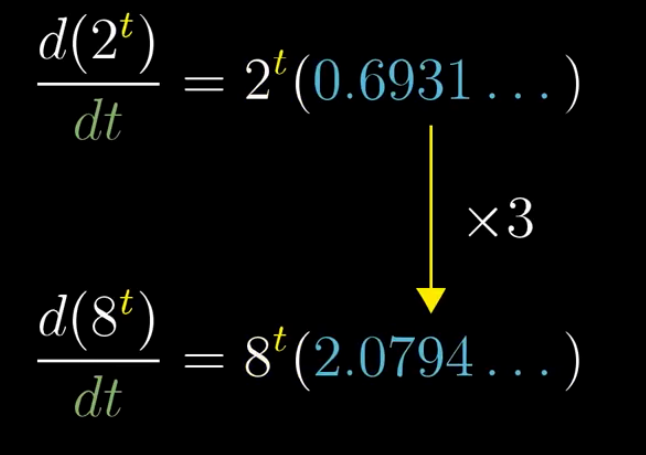
我们可以看到底数取的不同,这个固定常数的值也是不同的。
引出问题
有没有一个指数函数满足,它的导数就是它自身呢?即上面括号中的常数取值为1。
如果有,该指数函数的底数是多少呢?
有的,它就是特殊的常数e,取值大约是2.71828(就是常数e的定义)
也就是 e 它的导数还是它自身

自然对数
自然对数是以常数e为底数的对数,记作lnN(N>0)
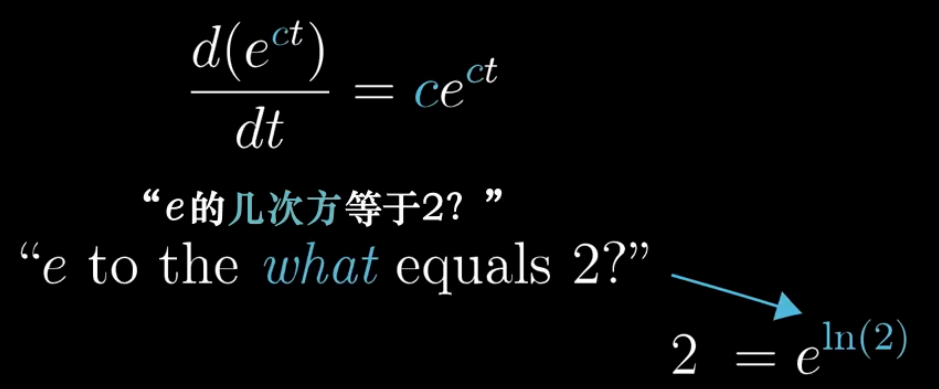
回忆几种说法:
1,以2为底,32的对数是多少?(答案是5,因为2的5次方为32)
2,以e为底,2的对数是多少?(也可以这样问,2的自然对数是多少)
问题就变换成了e的几次方等于2呢?那不就是ln2么,约等于0.6931。
求导大戏
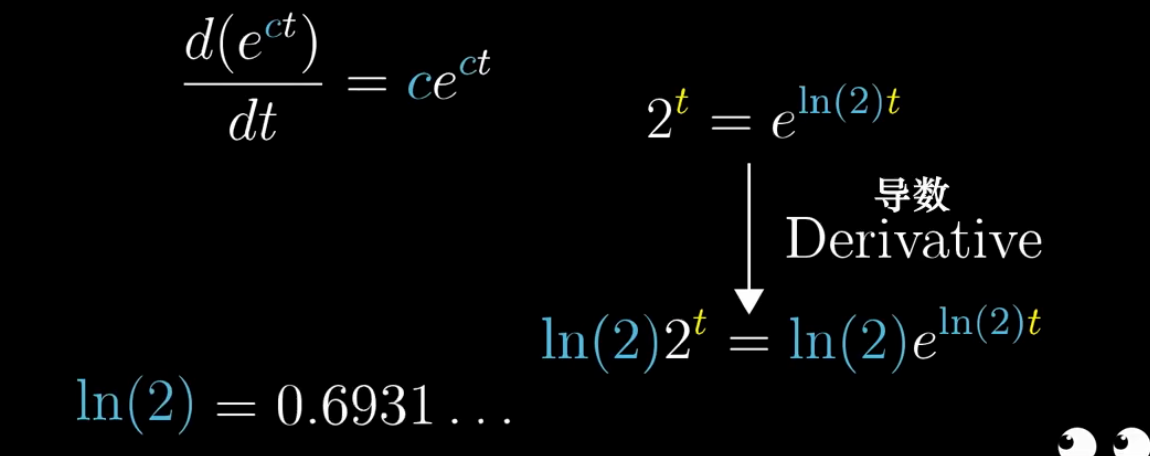
这里应用了我们之前学习过的链式法则。
注意一点:(2) = 2
惊艳一瞥
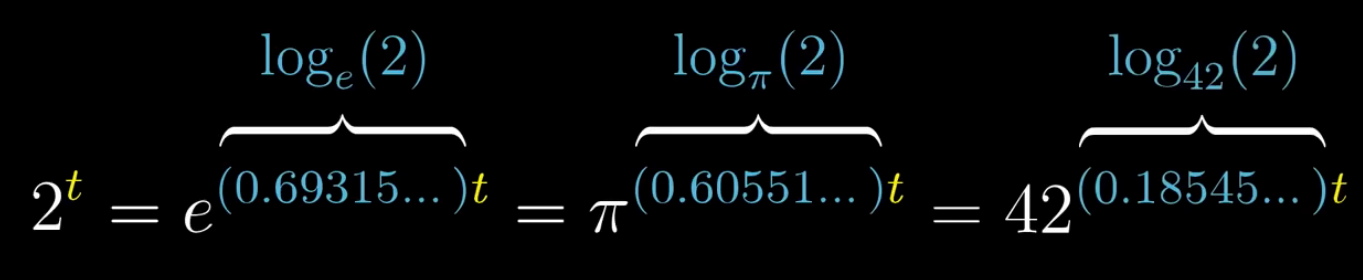
指数函数可以写成许多种不同的形式,之所以写成以自然常数为底的形式,是因为此时指数上的常数就有一目了然的意义。(比如就等于ln2,ln8等)
实例应用
指数函数的导数,即变化率和函数自身的比值是常数。
那投资来举例,甲有10万本金,年化10%,收益函数为 10 * (1 + 10%) ,其中 t 为年份
乙有100万本金,同样年化10%,收益函数为 100 * (1 + 10%) ,其中 t 为年份
前面的系数不同,所以这两个函数计算出来的导数(变化率)也不同,乙的变化率要比甲大10倍,应了常说的马太效应。
隐函数求导
如果方程F(x,y)=0能确定y是x的函数,那么称这种方式表示的函数是隐函数
x和y是同时由一个等式定义,而互相联系在一起的,不存在说输入一个x,就一定对应一个输出y
即满足某种关于变量x和y的性质,所有(x, y)点的集合
求斜率

根据上图,我们可以看到,在点(3, 4)这一点上切线的斜率为-3/4,右下角给出了一个大概的求解步骤,可是为什么这么求?
分别对dx和dy进行求导,求解出来的结果又有什么实际意义呢?
梯子问题
问题是这样的,长5米的梯子靠在墙上,靠近墙的这头以每秒1m的速度向下滑落,问在刚开始的瞬间,梯子底部向左移动的速度是多少?
我们把x和y都看成是关于时间t的函数,等式左右两边分别对时间dt进行求导,等式右边的常数是不随时间的变化而变化的,因此它求导的结果为0;等式左边的求导就如图中所示了。
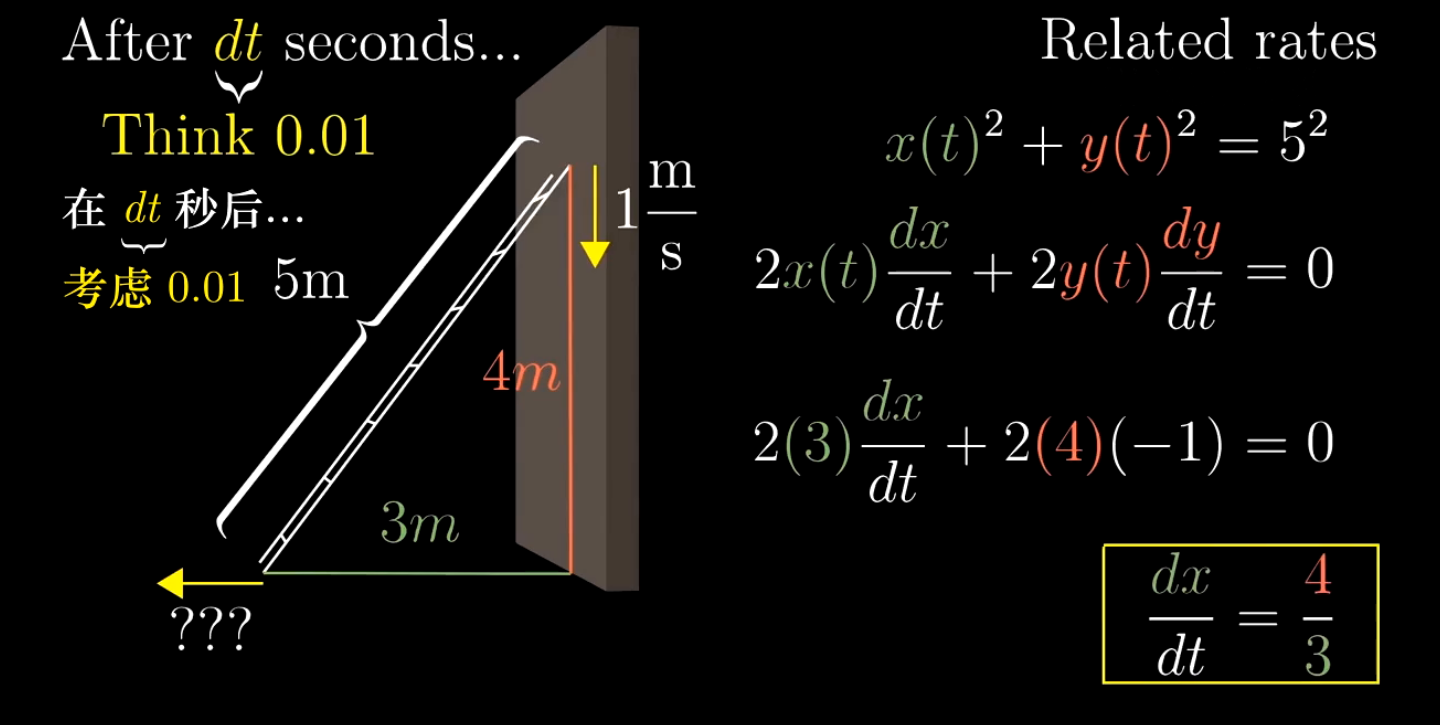
下面给出另外一种计算方式
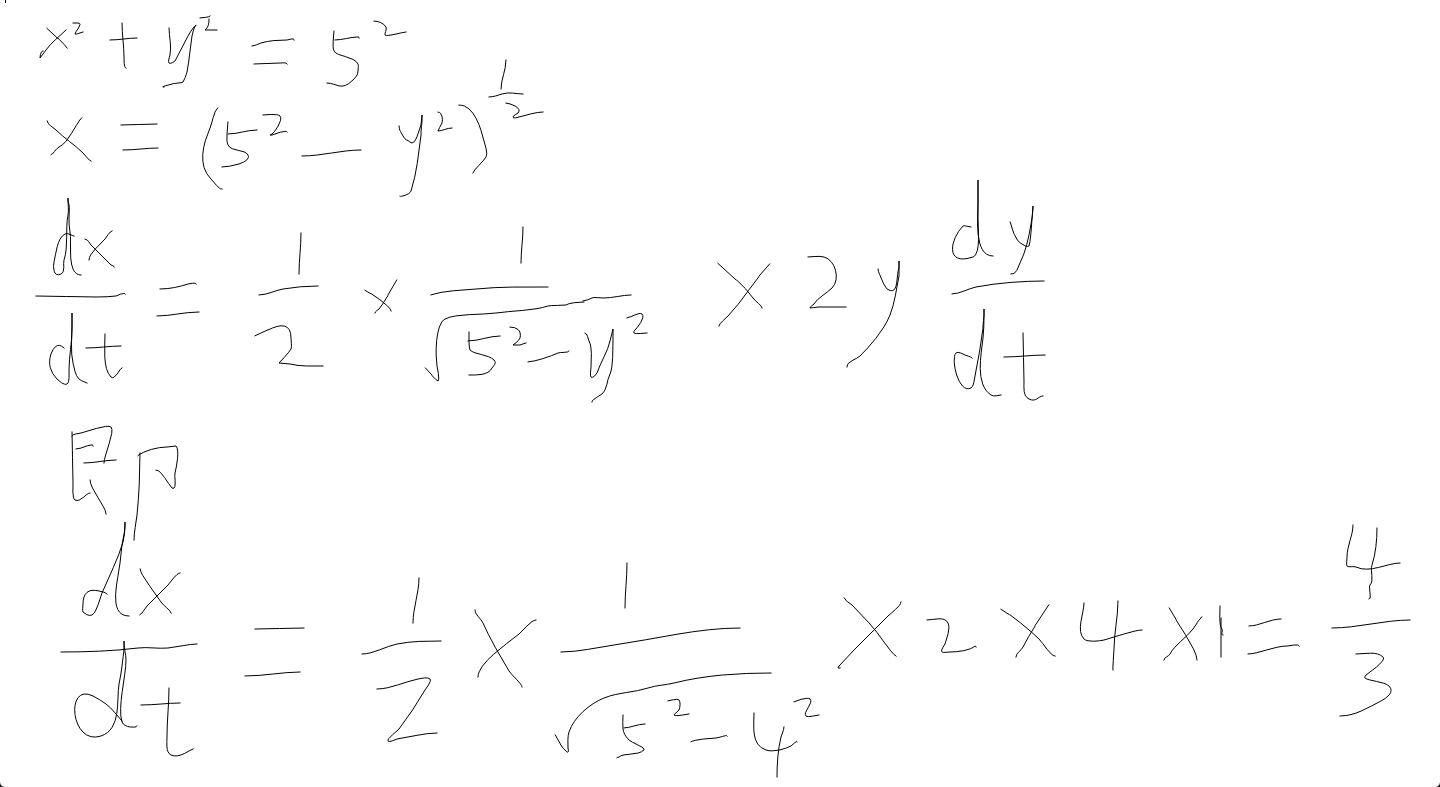
解释
我们令S = x + y,那么 dS 就表示平面上的点沿 x 轴方向行进dx,沿 y 轴方向行进dy后,S的变化量(近似值)。(此时我们并不局限在圆上的点,需要注意的一点是:dx和dy都是微小变化量)
对下图中的例子进行计算
刚开始点(3,4)对应的S值为25
沿x轴方向行进-0.02,沿y轴方向行进-0.01,到达点(2.98,3.99),对应的S值为24.8005
计算出来的差值为0.1995
而我们通过图中dS这种方式计算出来的值为0.2 (只是个近似值)
当dx和dy的值越小时,这两个值会越接近
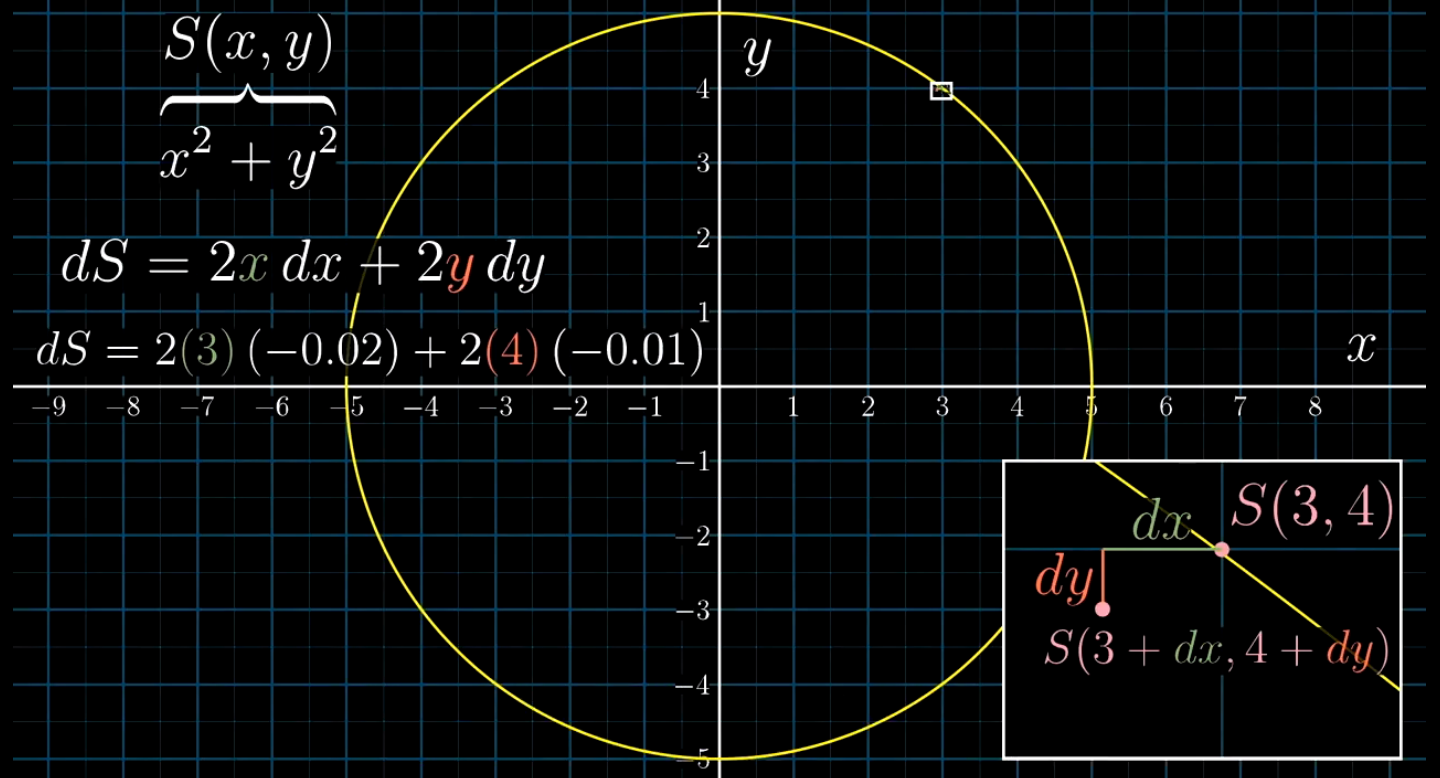
现在我们来考虑圆上的点,只要是圆上的点,都满足S值为25;换句话说,即S值没有变化,对应的dS值为0。
即 2xdx + 2ydy = 0
拓宽
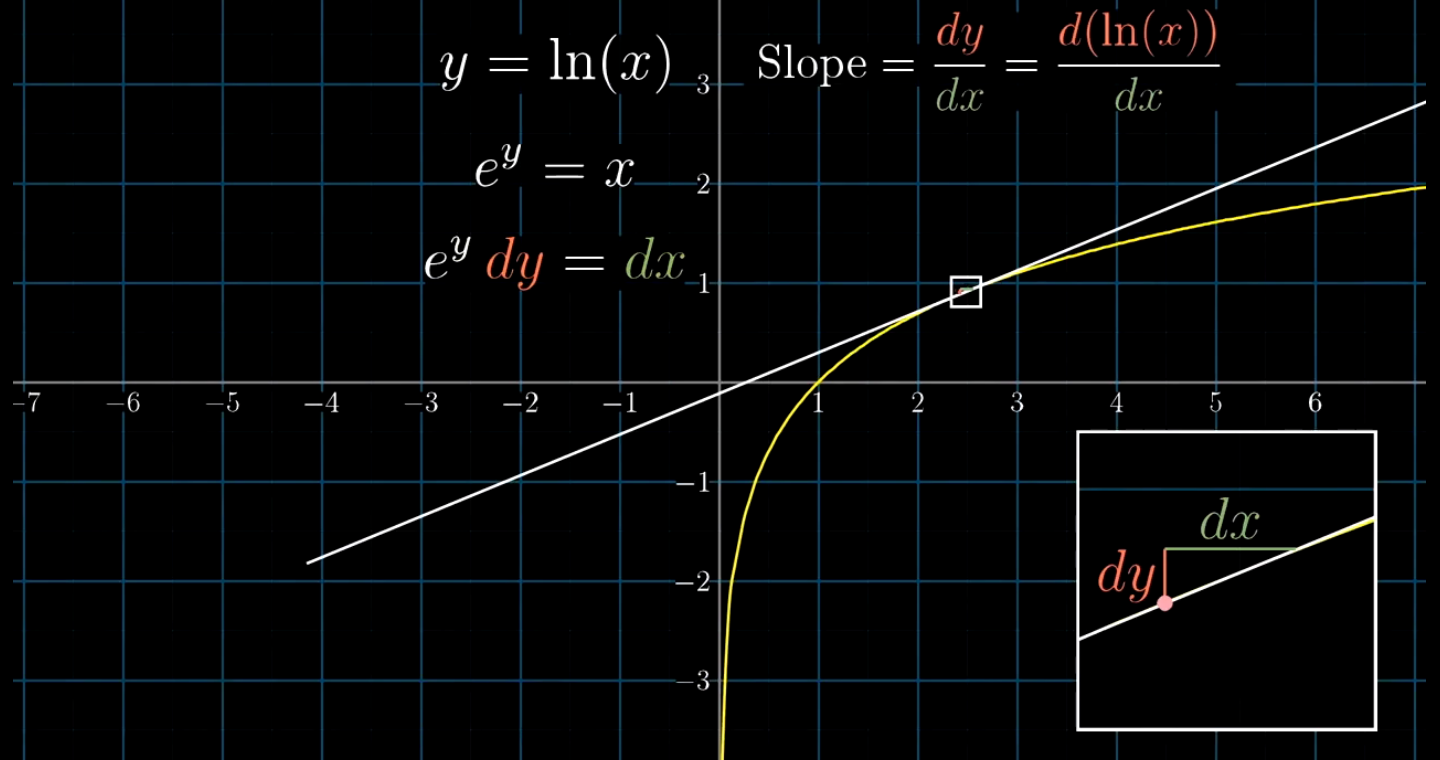
其中y是关于x自然对数的函数
我们将其转换为隐函数的形式,即 e = x
左右两边同时求导并移项,即 dy / dx = 1 / e = 1 / x
极限
微积分需要连续,而连续需要无穷小,但是没人能探明无穷小的样子
导数的正式定义

上图中的h和我们之前讲的dx是同一个东西,微小变化量,无线趋近于0,但不等于0.
极限的定义
一个变量逼近另一个变量的含义
下图中的方程曲线就是 ((2 + h) - 2) / h
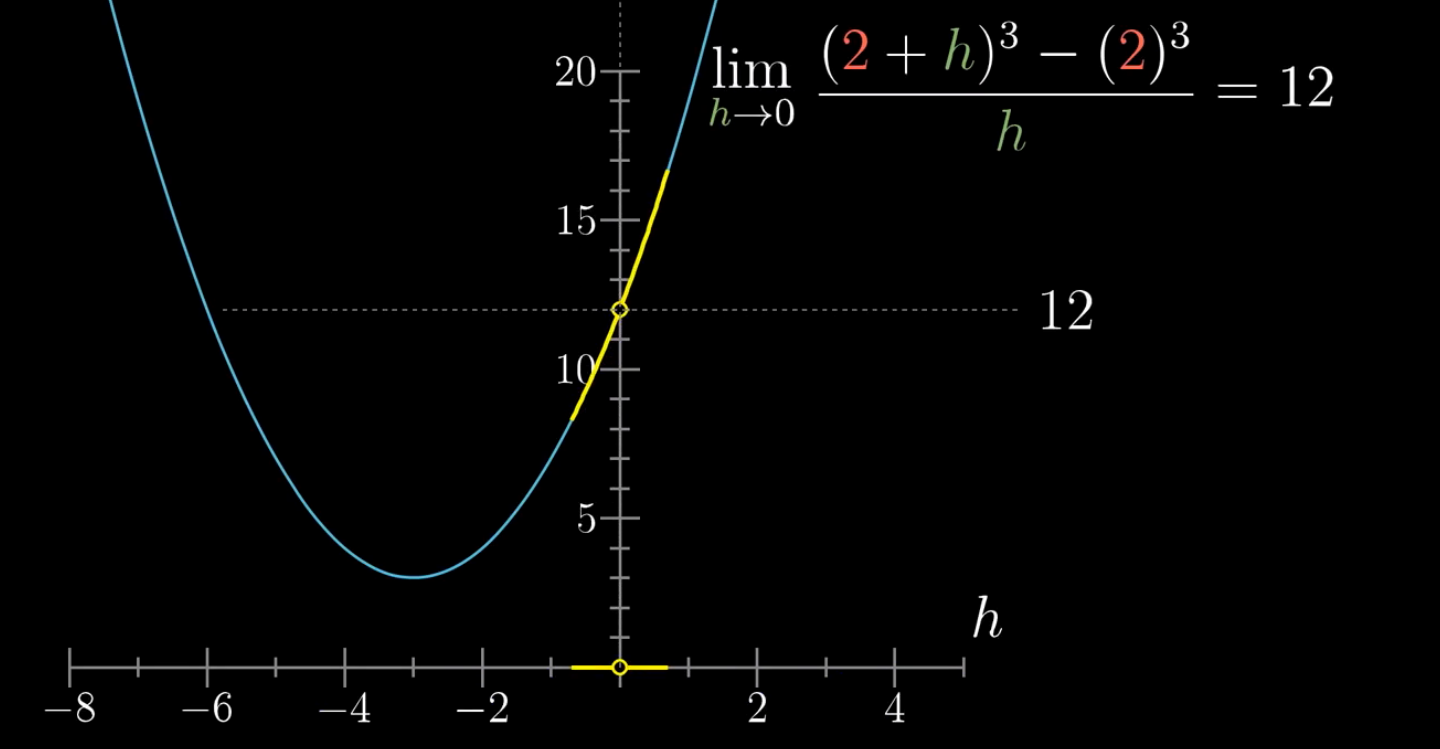
无论自变量是从1到0逼近,还是从-1到0进行逼近,
因变量的值最终逼近值12。
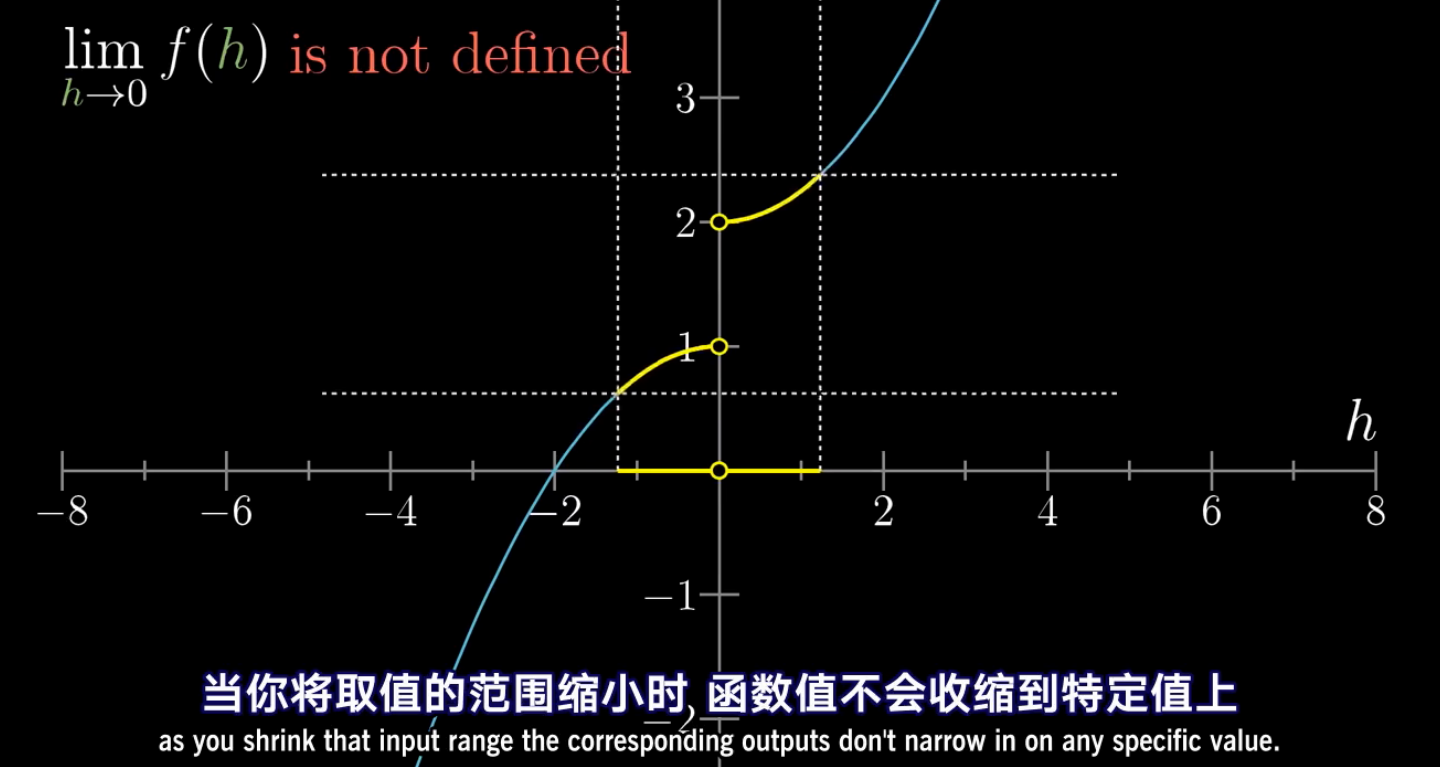
上面我们用极限定义了导数,那我们怎么来计算极限呢?
具体一点来讲,上面例子中的12是怎么计算出来的
洛必达法则
我们用极限定义了导数,导数也可以帮助我们来求极限。
看下图中的例子,我们要求当x趋近于1时,该方程趋近于多少?很明显我们不能直接代入,因为直接代入分母为0。
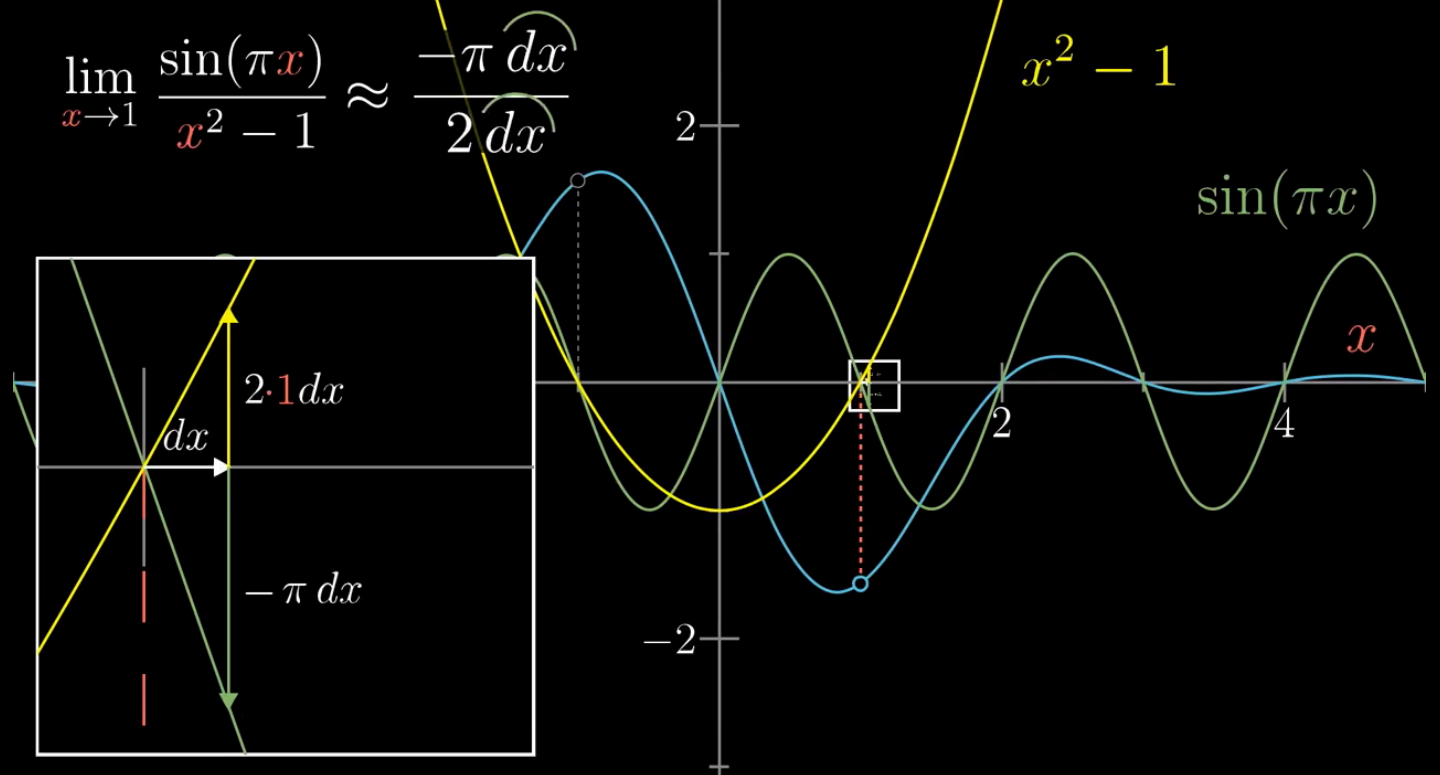
我们分别对分子和分母求导,然后再代入x=1,即可求出(求导后分子和分母中的dx可以约掉)
这就是洛必达法则(主要是针对0/0型的求极限)
在我们导数正式的定义小节,对分子求导就是3*x,对分母求导值为1,代入x=2,即求得结果为12。
积分与微积分
积分是求导的逆运算(求导是不断分割,积分是不断累加)
求积分的一般步骤
- 找到原函数F
- 分别计算上限和下限的值
- 相减即是结果
匀速行驶
先考虑一个比较简单的问题,汽车以恒定的速度10m/s行驶了8秒,问汽车行驶的距离是多少?

很好算,其实它对应的是上图中阴影部分的面积。我们可以将上图中的阴影面积看成8个小矩形,在每一秒内,用速度乘以时间就是距离,然后累加。
那如果是非匀速行驶,我们又该如何计算距离呢?
变速行驶
同样的思想,我们也可以应用到变速行驶上,随着dt取值越来越小,矩形框也会越来越多,计算的距离值也会越来越精确。

最后,问题就转化为了求解曲线与横轴围成的面积。(t从0到8)
深入理解
一方面,距离的微小变化量除以时间的微小变化量就是速度,对应速度函数
另一方面更加通用的解释是
看下图,当dT足够小时,面积的微小变化量ds就等于v(T)*dT,那ds对dT求导即v(T)
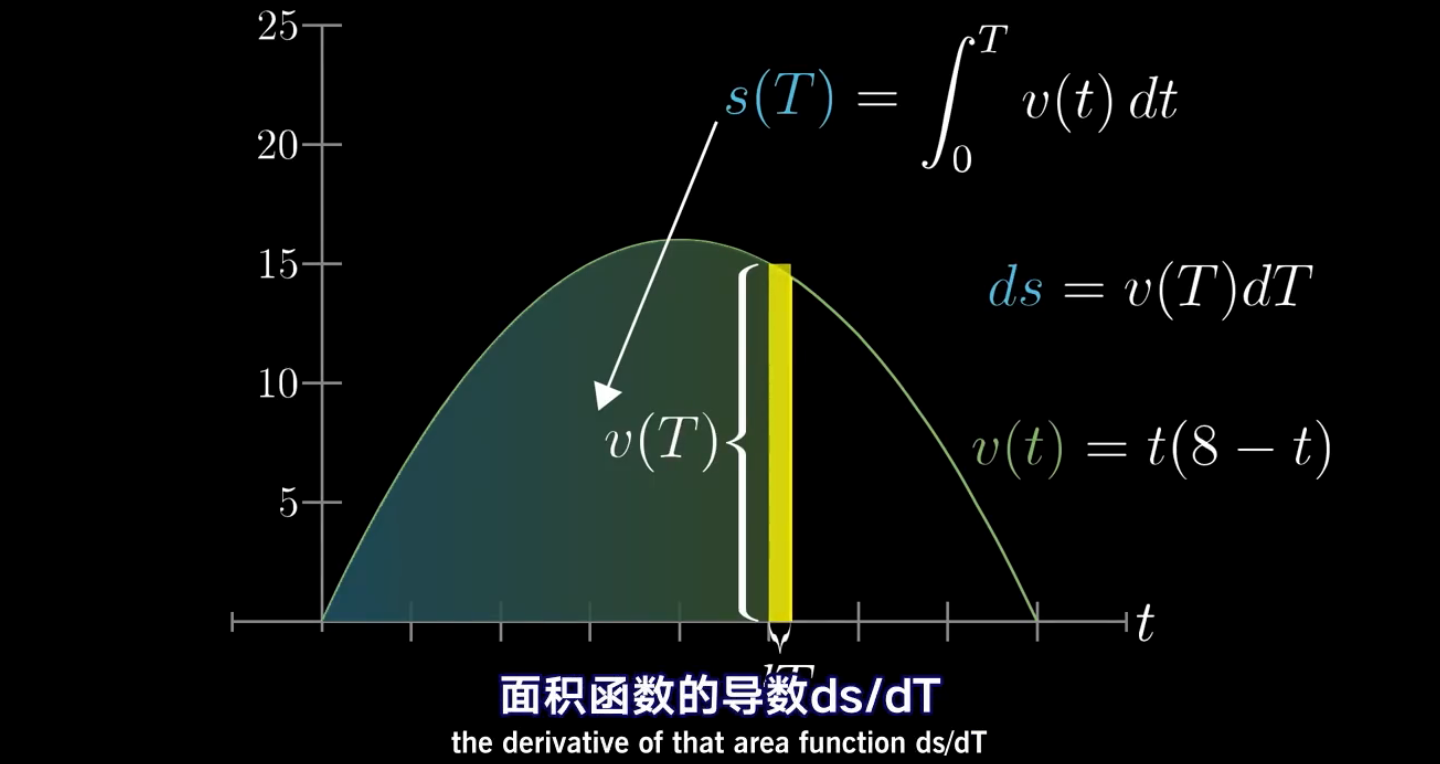
即任一函数图像下方面积的导数等于原先的函数本身
这样一来,我们计算面积就有思路了
哪个函数求导之后是 v(t)=t(8-t) 呢?即求它的原函数。
求解
很明显,我们知道针对上面的v(t),它的原函数为:
4 t + 1 / 3 t + C(常数)
虽然 v(t) 的原函数有许多个,因为常数的导数为0嘛;
但其实我们并不关心这个常数项,因为常数项在积分上限减下限的时候,会约掉。
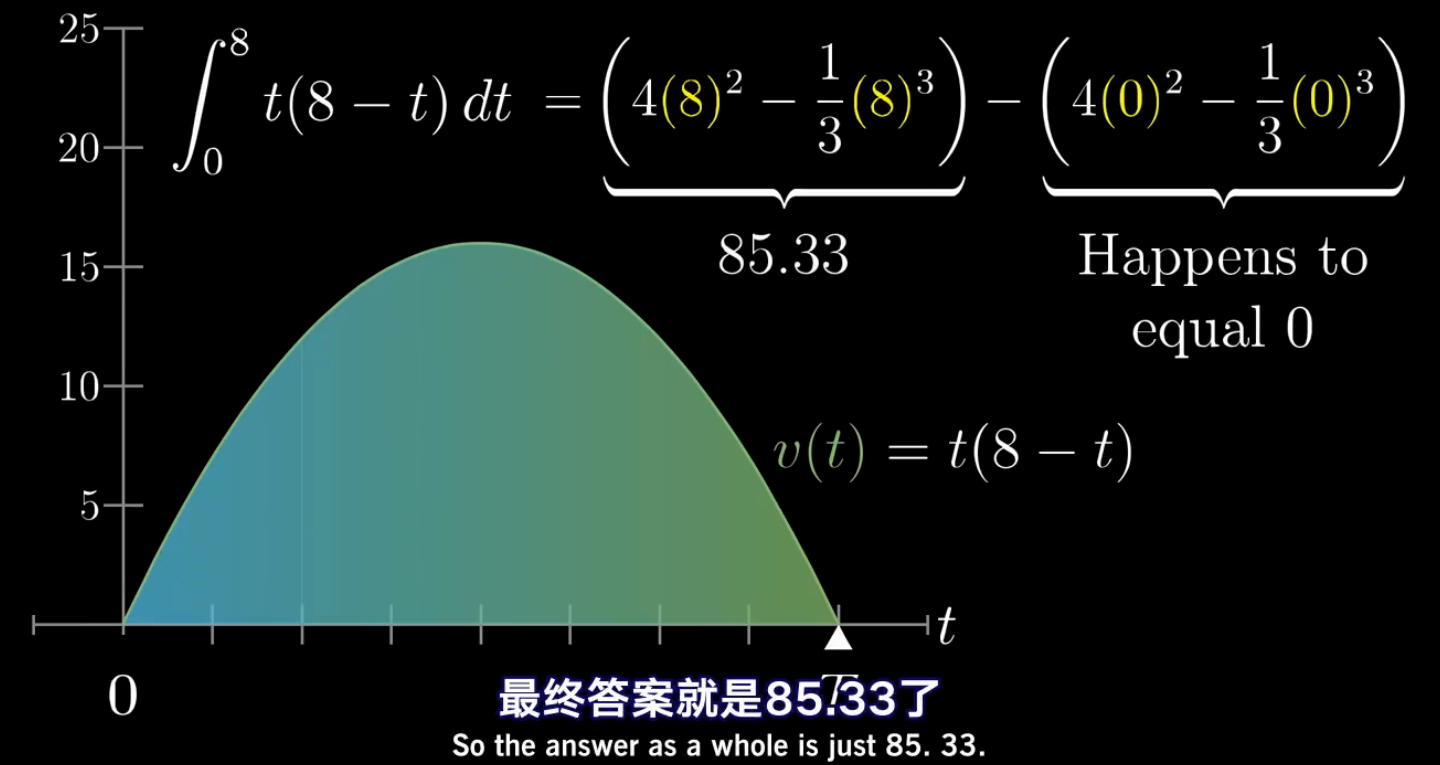
当然了,这个也可以推广到更一般的形式。
面积和斜率
连续变量求均值
这并不是一个没有意义的问题,我们想一想,连续型随机变量求期望,我们通常已知的是概率密度函数,不就是连续变量求平均值吗?
我们仔细看下方的图,暂时先考虑成有限个点,
分母就是有限点的个数,即 π / dx
分子就是图中矩形的高累加,到目前为止,所有的步骤都是清晰明了的
很关键的一步,就是将分母中的dx,移到分子上,有趣的事情发生了
分子是不是就变成了计算图中阴影部分所有矩形的面积,随着dx取值越来越小,分子就对应了曲线与横轴围成的面积(在区间[0, π]),分母就是区间的宽度 π
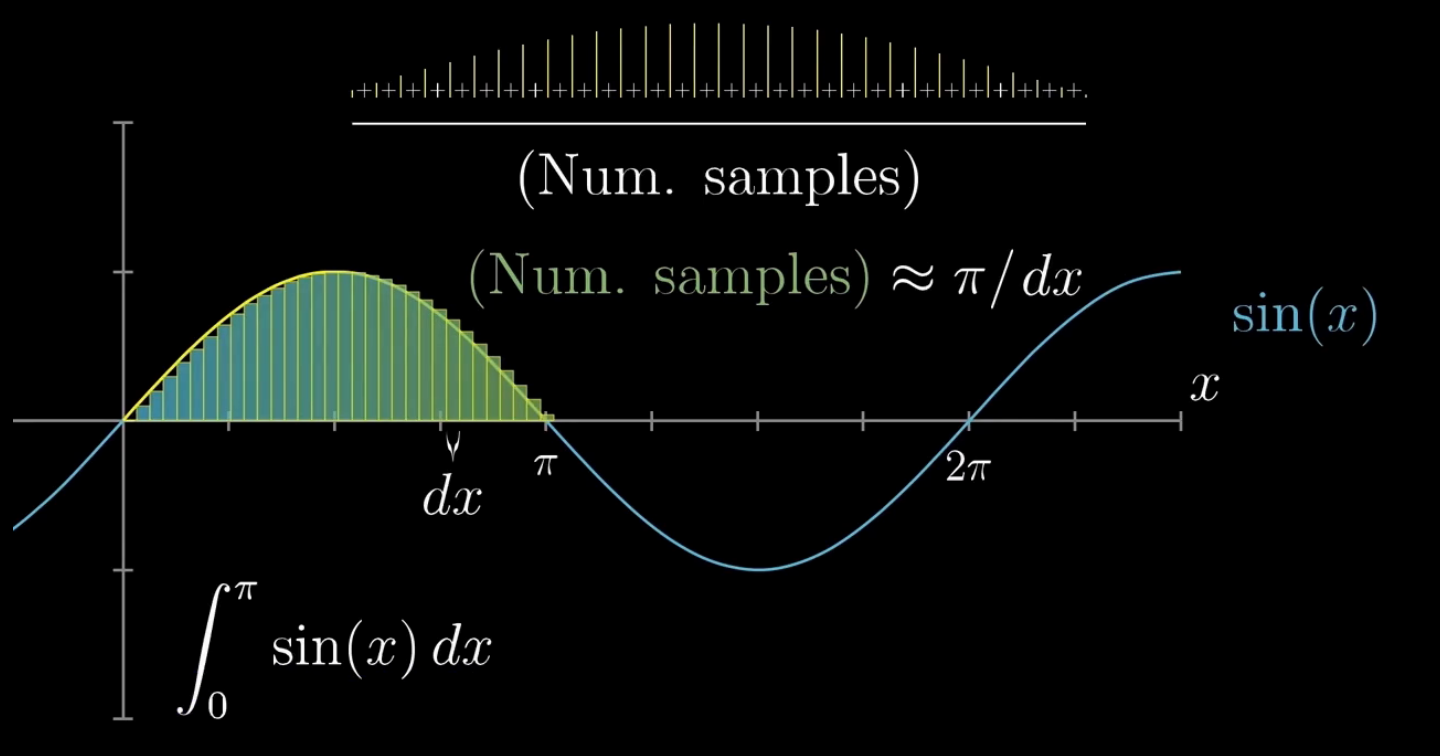
我们得出结论,即连续变量的均值就是 面积 / 区间宽度
针对图中的例子,我们计算得知函数 y = sin(x) 在区间[0, π]上的均值就为 2 / π
另一个视角
下图中绘制了sin(x)的原函数 -cos(x)的曲线,我们可以看到,
该连续变量在0~π上的平均值,刚好等于它对应的原函数在区间起点和区间终点两点连线的斜率。
也就是说原函数 -cos(x) 在区间[0, π] 之间所有切线斜率的平均值就是起点和终点两点连线的斜率。

我们来思考一下为什么?
原函数 -cos(x) 上每一点对应切线的斜率(我们可以考虑一个微小变化量dx),其实对应着 sin(x) 曲线下方一个小矩形的高。
所有的高累加 / 划分的数量 (其实又回到了上一小节连续变量求均值的思路)
高阶导数
二阶导数
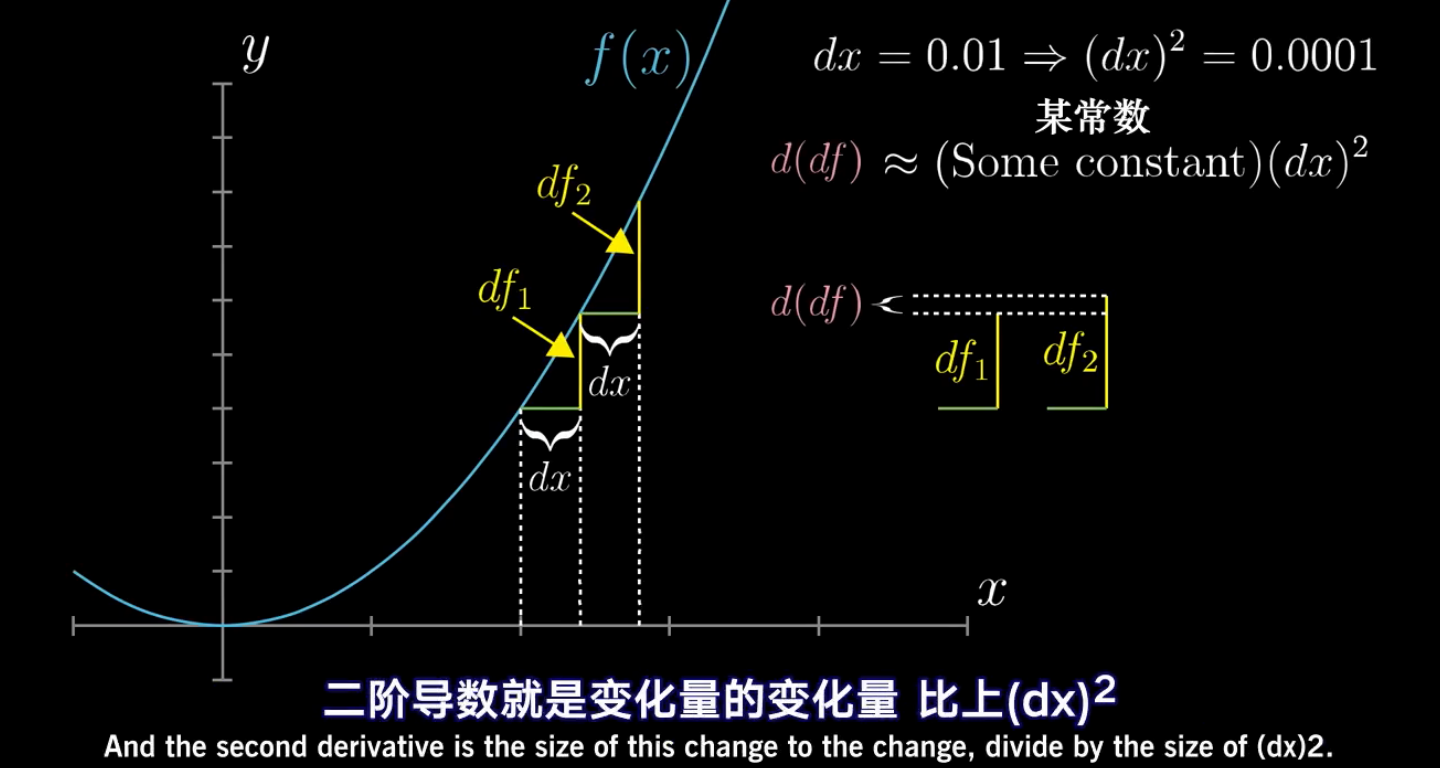
什么是二阶导数,可以理解为是导数的导数,两次求导
第一次求导对应的是曲线上点的斜率
第二次求导对应的是斜率变化的快慢
我们注意到分子上对df进行求导,产生了两个d,虽然d并不是一个可以直接相乘的变量,但我们为了简单起见,通常写成 df
而分母则是 (dx),通常情况下,我们会省略掉这个括号
加速度
加速度可能是我们理解二阶导数的最佳例子。
在下面的例子中,汽车行驶了一段距离,先加速后减速。
前半段二阶导数为正,表示速度在增加,速度曲线的斜率由0变大,再变为0
后半段二阶导数为负,表示速度在减少,速度曲线的斜率由0变小,再变为0
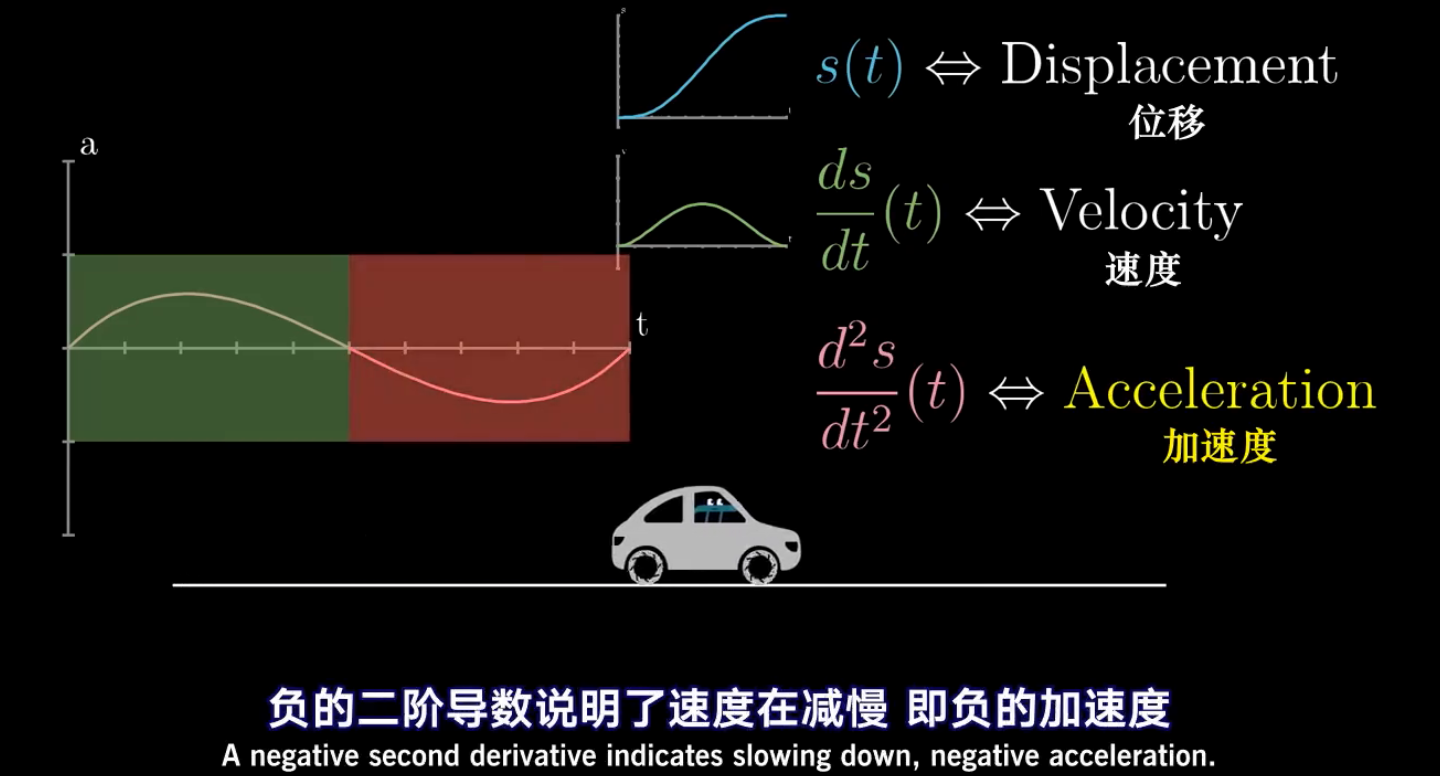
注意图中,二阶导数符号的写法。
泰勒级数
泰勒多项式
抛出一个问题,比方说一个函数 y = cos(x),我想用一个多项式去近似它,至少在 x = 0 附近,多项式的结果应该和cos(x)的结果是相差不大的。
那我们该如何解决这个问题呢?泰勒多项式就是用来干这个的。
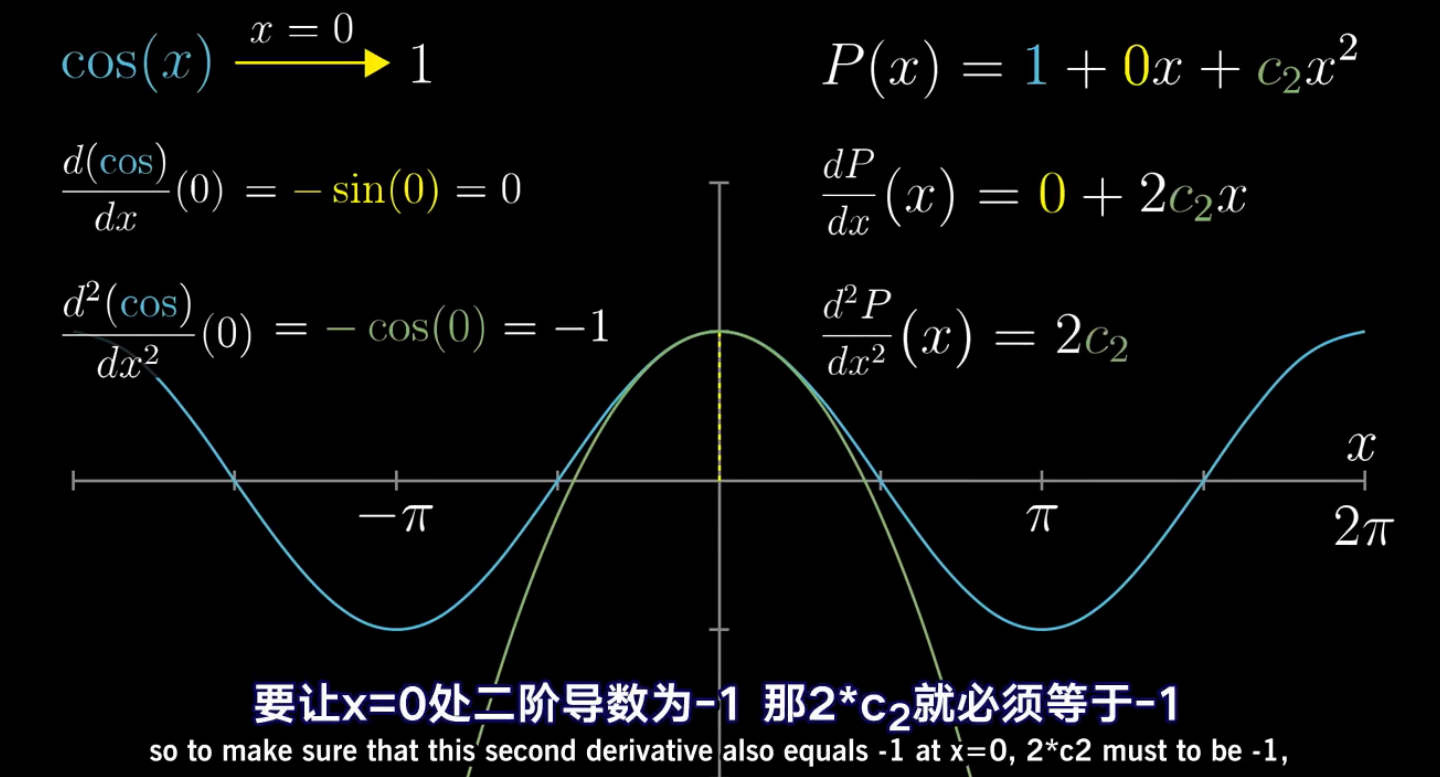
看上图中的三个步骤:
- 当x取值为0时,cos(x)取值为1,对应多项式也该取值为1;即常数项值为1
- 对cos(x)求一阶导数,在x=0处的斜率为0,对应多项式也作一阶导数,代入x=0值应该为0;进而计算出一次项系数应该为0
- 对cos(x)求二阶导数,表示斜率的变化率,在x=0处的值为-1,对应多项式求二阶导数值也应该为-1;进而计算出二次项系数应该为-1/2
我们粗略的估计了一个多项式,即1-1/2*x,当然我们还可以继续计算下去,求cos(x)的三阶导数和四阶导数,分别对应着多项式的三次项系数,和四次项系数。
经过计算,近似多项式的三次项系数为0,四次项系数为1/24。(当然我们还可以继续往下计算)
即我们估计近似cos(x)的多项式就是1- 1/2 x+ 1/24 x (这就是泰勒多项式的计算方式)
注意一点:如果估算的不是x=0这一点,比如x=a这点,把自变量设置成x-a就可以了
几何角度
首先,我们需要明确的一点是:下图中的f(x)表示的是关于曲线下方面积的函数
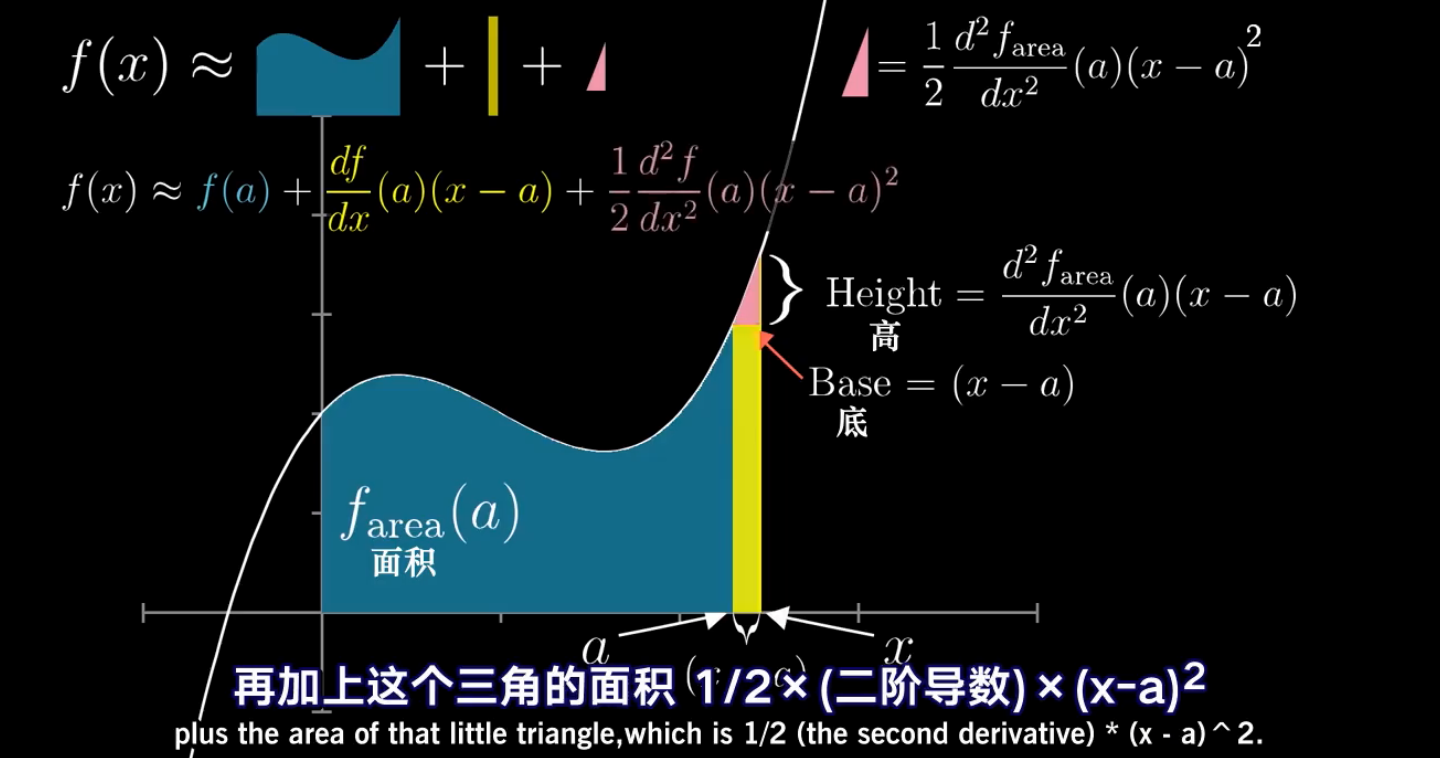
我们先解释一下黄色矩形的面积,宽是 x - a 这没疑问,高就是曲线在x = a处的取值了,而曲线函数是面积函数f(x)的一阶导数,即df对dx求导,然后代入x = a即是黄色小矩形的高
我们再解释一下三角形面积的计算,宽没问题,高是曲线函数在x = a处的斜率乘以dx,即乘以 x - a(斜率 = dy / dx),曲线函数是面积函数的一阶导数,曲线函数的斜率自然是面积函数的二阶导数了。所以三角形高的取值就如图中所示了。
这是不是和二次的泰勒多项式有些像呢?
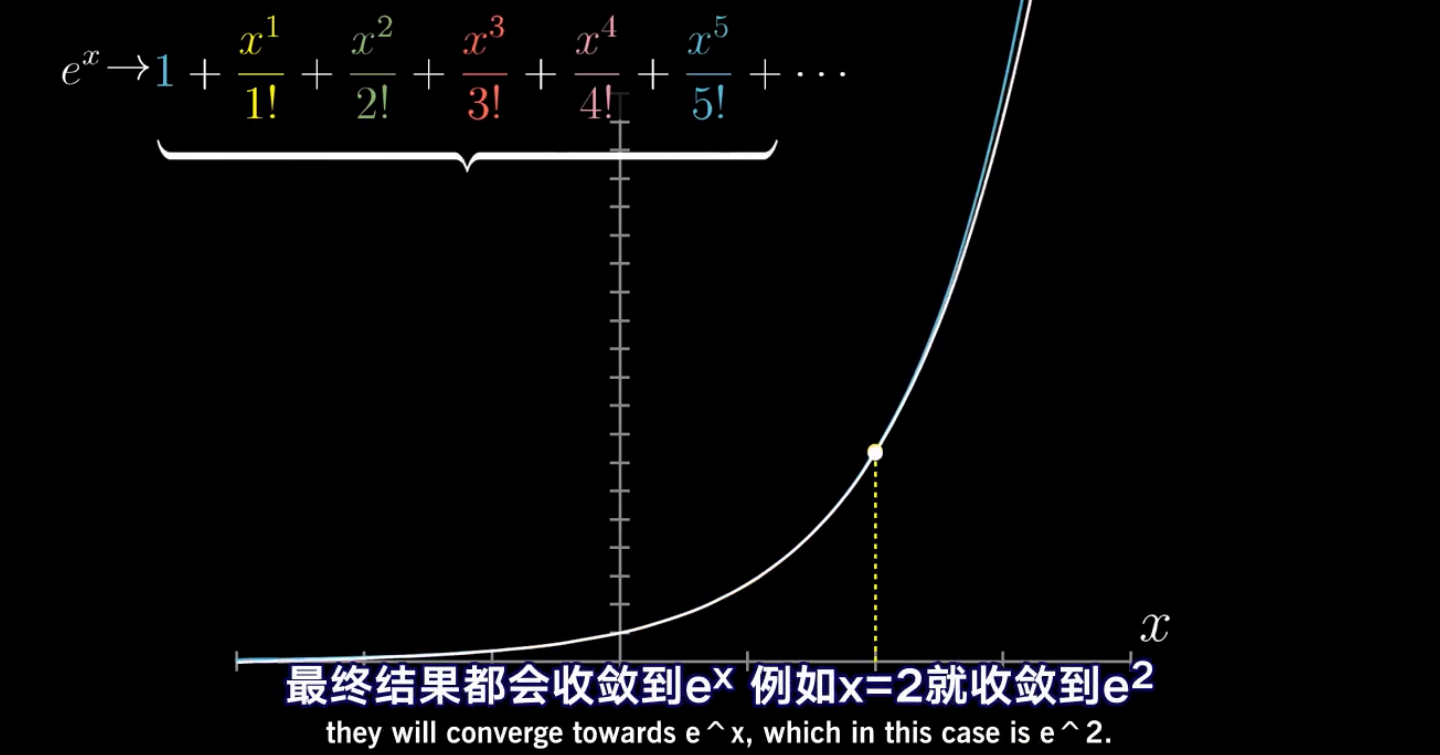
收敛
满足某种规律的多项式(级数),随着多项式越加越多,最终收敛于某个值,我们成它是收敛的
否则,我们称它为发散的
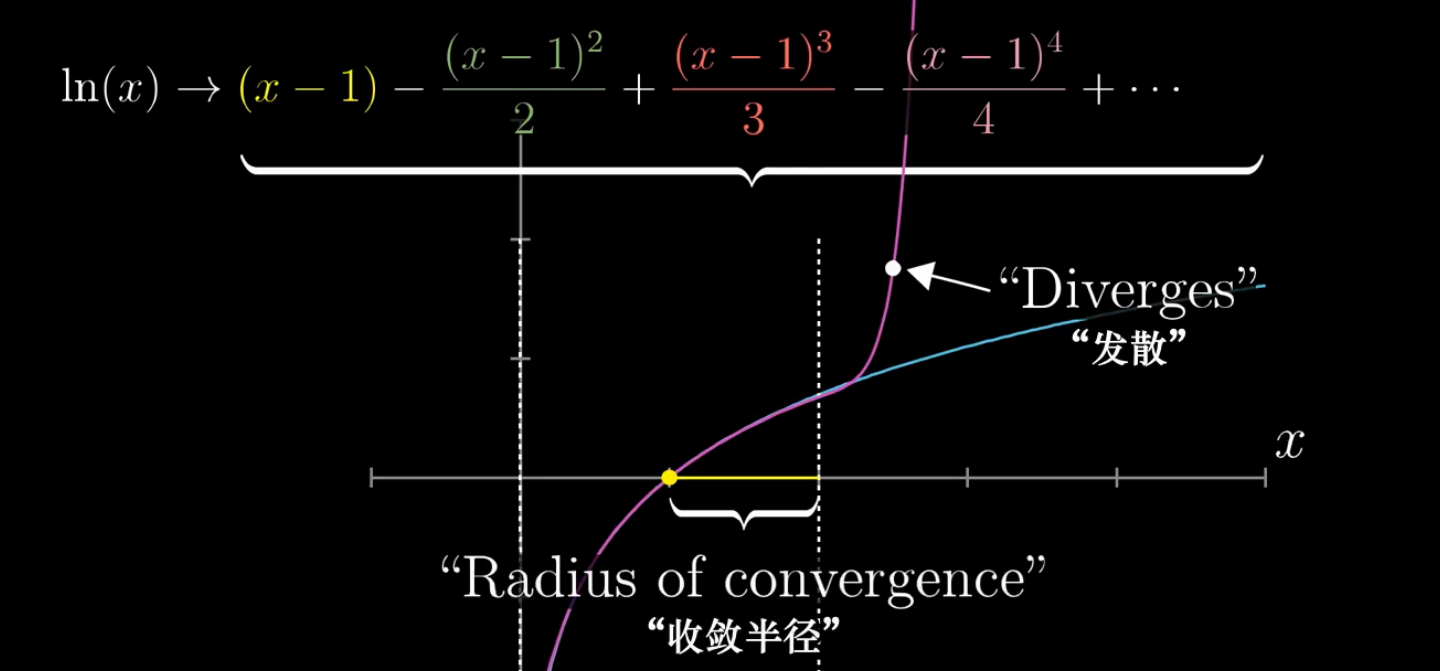
补充
之前,我们是近似cos(x)当x等于0时的多项式,下面我们近似当x等于π时的多项式。是同样的道理。
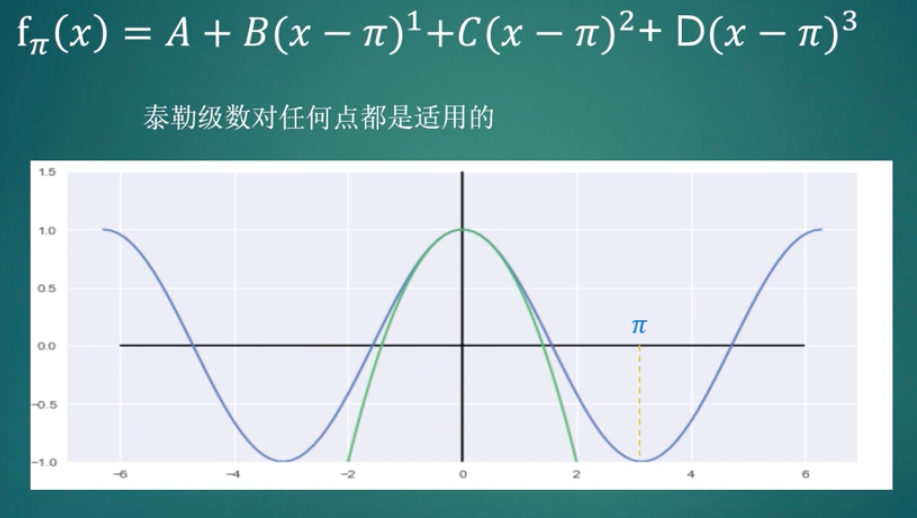
推广到一般情况
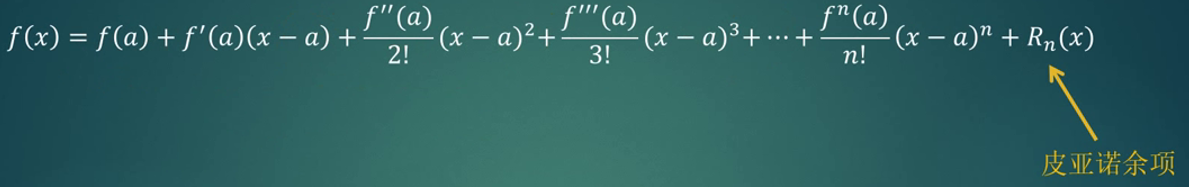
皮亚诺余项被解释为误差项
**
我们可以感受到,当我们在求n阶倒数时,多项式中小于等于n-1的项都会被消掉了
在实际应用中,我们一般只近似到2次项,3次项就可以了。

