简述

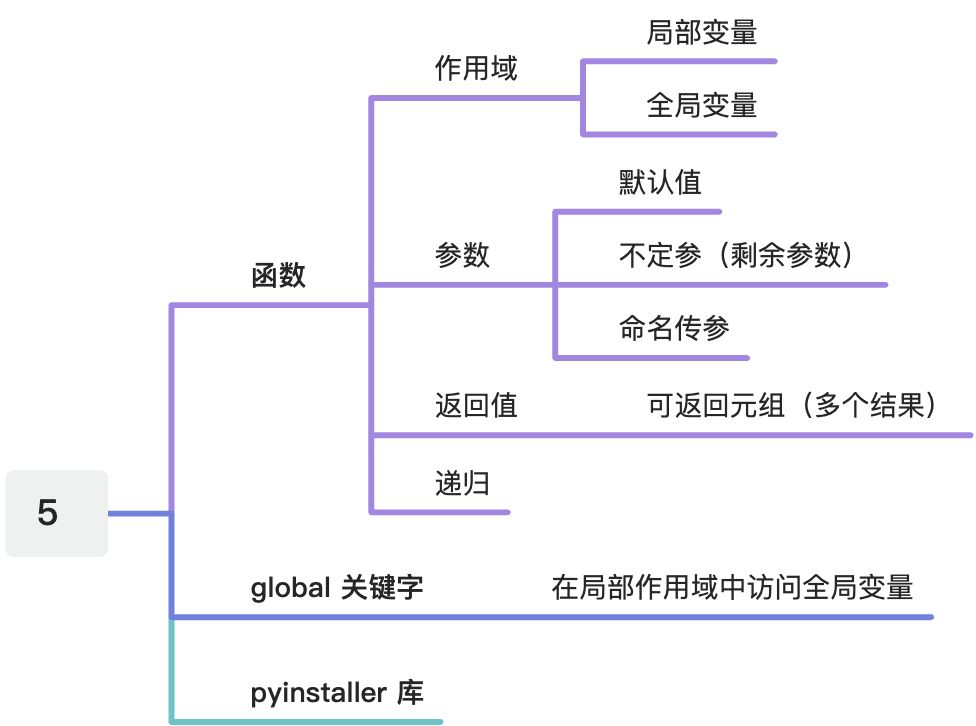
5. 函数和代码复用 - 图1

掌握函数的基本使用方法，理解并掌握递归使用，掌握PyInstaller库，能够编写带有函数的程序，并能够打包可执行文件。

课件

5.pdf

代码汇总

  1. def dayUP(df):
  2.     dayup = 1
  3.     for i in range(365):
  4.         if i % 7 in [6, 0]:
  5.             dayup = dayup * (1 - 0.01)
  6.         else:
  7.             dayup = dayup * (1 + df)
  8.     return dayup
  11. dayfactor = 0.01
  12. while dayUP(dayfactor) < 37.78: # 37.78 是一年每天努力 1% 的结果
  13.     dayfactor += 0.001
  14. print("工作日的努力参数是：{:.3f} ".format(dayfactor))
  15. # 工作日的努力参数是：0.019
  1. def fact(n):
  2.     s = 1
  3.     for i in range(1, n + 1):
  4.         s *= i
  5.     return s
  8. a = fact(10)
  10. print(a) # 3628800
  1. def fact(n, m=1): # 可选参数、参数默认值
  2.     s = 1
  3.     for i in range(1, n + 1):
  4.         s *= i
  5.     return s // m
  8. print(fact(10))  # 3628800
  9. print(fact(10, 5))  # 725760
  1. def fact(n, *b): # 可变参数
  2.     s = 1
  3.     for i in range(1, n + 1):
  4.         s *= i
  5.     for item in b:
  6.         s *= item
  7.     return s
  10. print(fact(10, 3))  # 10886400
  11. print(fact(10, 3, 5, 8))  # 435456000
  1. def fact(n, m=1):
  2.     s = 1
  3.     for i in range(1, n + 1):
  4.         s *= i
  5.     return s // m
  8. # 传参：位置传递
  9. print(fact(10, 5))  # 725760
  10. # 传参：名称传递
  11. print(fact(m=5, n=10))  # 725760
  1. def fact(n, m=1):
  2.     s = 1
  3.     for i in range(1, n + 1):
  4.         s *= i
  5.     return s // m, n, m # 返回多个结果
  8. print(fact(10, 5))  # (725760, 10, 5)
  9. # 返回结果 (725760, 10, 5) 是一个 元组类型
  11. # 定义变量接收返回结果
  12. a, b, c = fact(10, 5)
  13. print(a, b, c) # 725760 10 5
  1. n, s = 10, 100  # n 和 s 是全局变量
  4. def fact(n):  # fact() 函数中的 n 和 s 是局部变量
  5.     s = 1
  6.     for i in range(1, n + 1):
  7.         s *= i
  8.     return s
  11. # 访问到的是全局变量 n 10 s 100
  12. print(fact(n), s) # 3628800 100
  1. n, s = 10, 100
  4. def fact(n):
  5.     # s = 1 # 局部变量
  6.     global s  # 使用全局变量 s
  7.     for i in range(1, n + 1):
  8.         s *= i
  9.     return s
  12. print(fact(n), s)  # 362880000 362880000
  1. ls = ["F", "f"]
  4. def func(a):
  5.     ls.append(a)
  6.     return
  9. func("C")
  10. print(ls)  # ['F', 'f', 'C']
  1. ls = ["F", "f"]
  4. def func(a):
  5.     ls = []
  6.     ls.append(a)
  7.     print(ls) # ['C']
  8.     return
  11. func("C")
  12. print(ls)  # ['F', 'f']
  1. f = lambda x, y: x + y
  2. print(f(10, 15)) # 25
  1. f = lambda: "lambda函数"
  2. print(f()) # lambda函数
  1. import turtle
  4. def drawLine(draw):  # 绘制单段数码管
  5.     turtle.pendown() if draw else turtle.penup()
  6.     turtle.fd(40)
  7.     turtle.right(90)
  10. def drawDigit(digit):  # 根据数字绘制七段数码管
  11.     drawLine(True) if digit in [2, 3, 4, 5, 6, 8, 9] else drawLine(False)
  12.     drawLine(True) if digit in [0, 1, 3, 4, 5, 6, 7, 8, 9] else drawLine(False)
  13.     drawLine(True) if digit in [0, 2, 3, 5, 6, 8, 9] else drawLine(False)
  14.     drawLine(True) if digit in [0, 2, 6, 8] else drawLine(False)
  15.     turtle.left(90)
  16.     drawLine(True) if digit in [0, 4, 5, 6, 8, 9] else drawLine(False)
  17.     drawLine(True) if digit in [0, 2, 3, 5, 6, 7, 8, 9] else drawLine(False)
  18.     drawLine(True) if digit in [0, 1, 2, 3, 4, 7, 8, 9] else drawLine(False)
  19.     turtle.left(180)
  20.     turtle.penup()
  21.     turtle.fd(20)
  24. def drawDate(date):  # 获得要输出的数字
  25.     for i in date:
  26.         drawDigit(eval(i))  # 通过eval()函数将数字变为整数
  29. def main():
  30.     turtle.setup(800, 350, 200, 200)
  31.     turtle.penup()
  32.     turtle.fd(-300)
  33.     turtle.pensize(5)
  34.     drawDate("20181010")
  35.     turtle.hideturtle()
  36.     turtle.done()
  39. main()

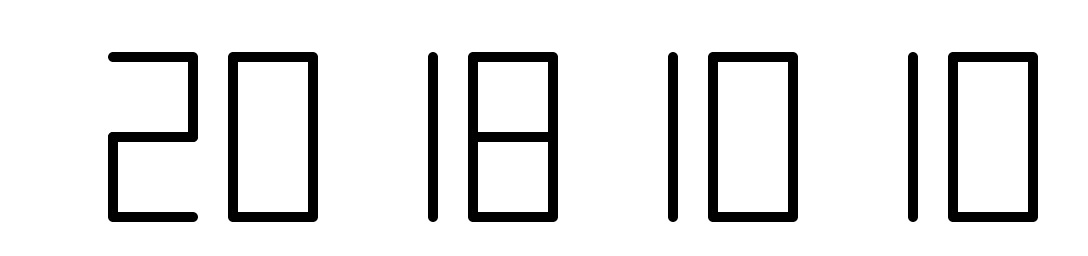
image.png

  1. import turtle, time
  4. def drawGap():  # 绘制数码管间隔
  5.     turtle.penup()
  6.     turtle.fd(5)
  9. def drawLine(draw):  # 绘制单段数码管
  10.     drawGap()
  11.     turtle.pendown() if draw else turtle.penup()
  12.     turtle.fd(40)
  13.     drawGap()
  14.     turtle.right(90)
  17. def drawDigit(d):  # 根据数字绘制七段数码管
  18.     drawLine(True) if d in [2, 3, 4, 5, 6, 8, 9] else drawLine(False)
  19.     drawLine(True) if d in [0, 1, 3, 4, 5, 6, 7, 8, 9] else drawLine(False)
  20.     drawLine(True) if d in [0, 2, 3, 5, 6, 8, 9] else drawLine(False)
  21.     drawLine(True) if d in [0, 2, 6, 8] else drawLine(False)
  22.     turtle.left(90)
  23.     drawLine(True) if d in [0, 4, 5, 6, 8, 9] else drawLine(False)
  24.     drawLine(True) if d in [0, 2, 3, 5, 6, 7, 8, 9] else drawLine(False)
  25.     drawLine(True) if d in [0, 1, 2, 3, 4, 7, 8, 9] else drawLine(False)
  26.     turtle.left(180)
  27.     turtle.penup()
  28.     turtle.fd(20)
  31. def drawDate(date):
  32.     turtle.pencolor("red")
  33.     for i in date:
  34.         if i == "-":
  35.             turtle.write("年", font=("Arial", 18, "normal"))
  36.             turtle.pencolor("green")
  37.             turtle.fd(40)
  38.         elif i == "=":
  39.             turtle.write("月", font=("Arial", 18, "normal"))
  40.             turtle.pencolor("blue")
  41.             turtle.fd(40)
  42.         elif i == "+":
  43.             turtle.write("日", font=("Arial", 18, "normal"))
  44.         else:
  45.             drawDigit(eval(i))
  48. def main():
  49.     turtle.setup(800, 350, 200, 200)
  50.     turtle.penup()
  51.     turtle.fd(-350)
  52.     turtle.pensize(5)
  53.     #    drawDate('2018-10=10+')
  54.     drawDate(time.strftime("%Y-%m=%d+", time.gmtime()))
  55.     turtle.hideturtle()
  56.     turtle.done()
  59. main()

image.png

  1. def fact(n):
  2.     if n == 0:
  3.         return 1
  4.     else:
  5.         return n * fact(n - 1)
  8. print(fact(0))  # 1
  9. print(fact(1))  # 1
  10. print(fact(2))  # 2
  11. print(fact(3))  # 6
  12. print(fact(4))  # 24
  13. print(fact(5))  # 120
  1. def rvs(s):
  2.     if s == "":
  3.         return s
  4.     else:
  5.         return rvs(s[1:]) + s[0]
  6. # s[::-1]
  1. def f(n):
  2.     if n == 1 or n == 2:
  3.         return 1
  4.     else:
  5.         return f(n - 1) + f(n - 2)
  1. count = 0
  4. def hanoi(n, src, dst, mid):
  5.     global count
  6.     if n == 1:
  7.         print("{}:{} -> {}".format(1, src, dst))
  8.         count += 1
  9.     else:
  10.         hanoi(n - 1, src, mid, dst)
  11.         print("{}:{} -> {}".format(n, src, dst))
  12.         count += 1
  13.         hanoi(n - 1, mid, dst, src)
  16. hanoi(3, 'A', 'B', 'C')
  18. ''' 
  19. 1:A -> B
  20. 2:A -> C
  21. 1:B -> C
  22. 3:A -> B
  23. 1:C -> A
  24. 2:C -> B
  25. 1:A -> B
  26. '''
  1. import turtle
  4. def koch(size, n):
  5.     if n == 0:
  6.         turtle.fd(size)
  7.     else:
  8.         for angle in [0, 60, -120, 60]:
  9.             turtle.left(angle)
  10.             koch(size / 3, n - 1)
  13. def main():
  14.     turtle.setup(800, 400)
  15.     turtle.penup()
  16.     turtle.goto(-300, -50)
  17.     turtle.pendown()
  18.     turtle.pensize(2)
  19.     koch(600, 3)  # 0阶科赫曲线长度，阶数
  20.     turtle.hideturtle()
  21.     turtle.done()
  24. main()

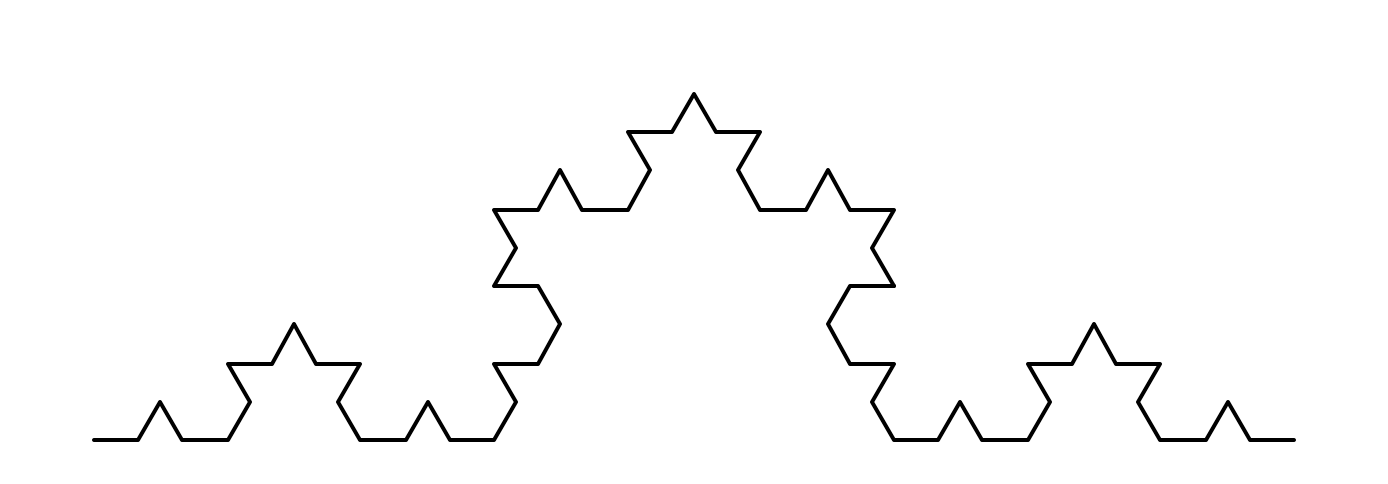
image.png

  1. import turtle
  4. def koch(size, n):
  5.     if n == 0:
  6.         turtle.fd(size)
  7.     else:
  8.         for angle in [0, 60, -120, 60]:
  9.             turtle.left(angle)
  10.             koch(size / 3, n - 1)
  13. def main():
  14.     turtle.setup(600, 600)
  15.     turtle.penup()
  16.     turtle.goto(-200, 100)
  17.     turtle.pendown()
  18.     turtle.pensize(2)
  19.     level = 3  # 3阶科赫雪花，阶数
  20.     koch(400, level)
  21.     turtle.right(120)
  22.     koch(400, level)
  23.     turtle.right(120)
  24.     koch(400, level)
  25.     turtle.hideturtle()
  26.     turtle.done()
  29. main()

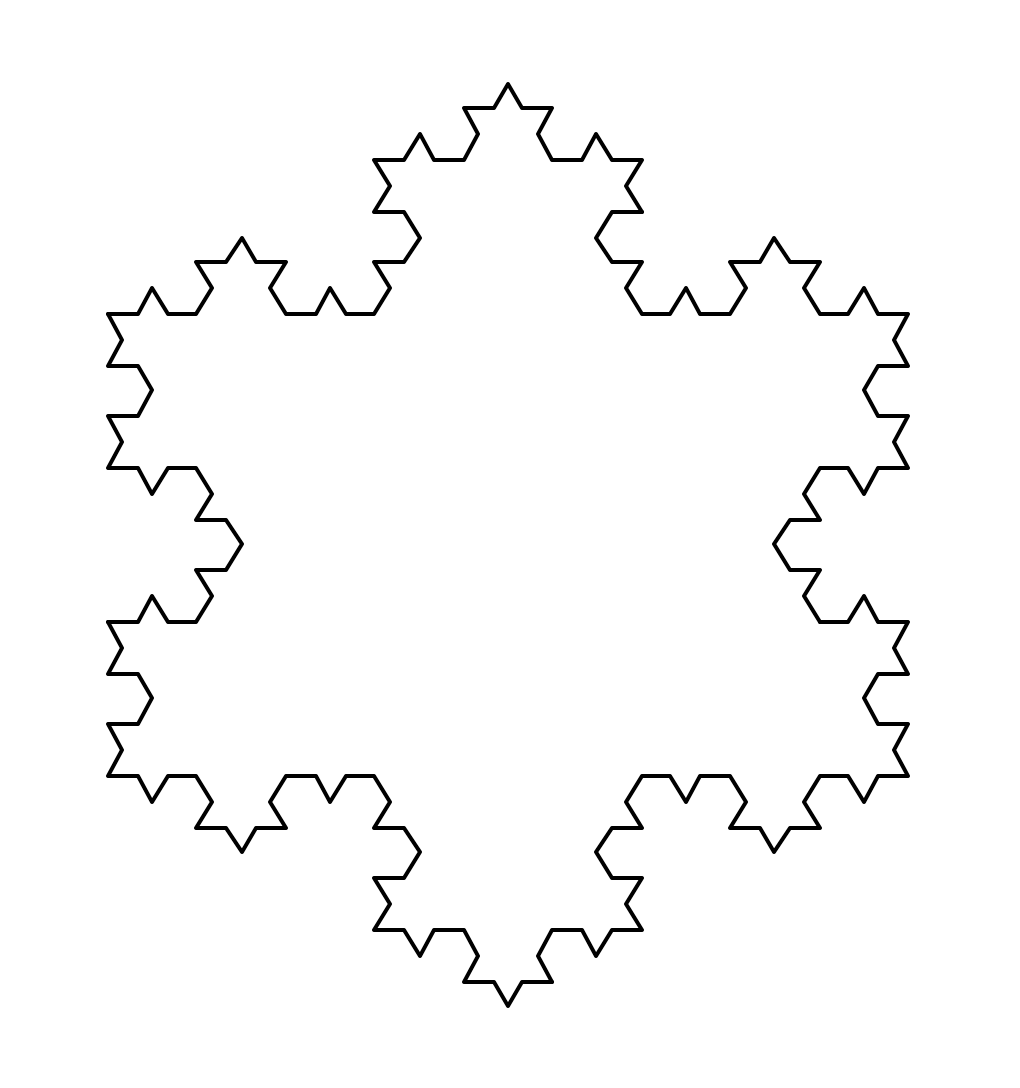
image.png

  1. def f(a, b):
  2.     a = 4
  3.     return a + b
  6. def main():
  7.     a = 5
  8.     b = 6
  9.     print(f(a, b), a + b)
  12. main() # 10 11
  1. def func(a, b):
  2.     c = a ** 2 + b
  3.     b = a
  4.     return c
  7. a = 10
  8. b = 100
  9. c = func(a, b) + a
  11. print(a, b, c) # 10 100 210
  1. def prime(m):
  2.     for i in range(2, m):
  3.         if m % i == 0:
  4.             return False
  5.     return True
  8. n = eval(input())
  9. n_ = int(n)
  10. n_ = n_ + 1 if n_ < n else n_
  11. count = 5
  13. while count > 0:
  14.     if prime(n_):
  15.         if count > 1:
  16.             print(n_, end=",")
  17.         else:
  18.             print(n_, end="")
  19.         count -= 1
  20.     n_ += 1
  22. """
  23. 12
  24. 13,17,19,23,29
  25. """
  1. def cmul(a, *b):
  2.     m = a
  3.     for i in b:
  4.         m *= i
  5.     return m
  8. print(eval("cmul({})".format(input())))
  10. """
  11. 1,2,3,4
  12. 24
  13. """

第 5 周导学

前课复习

[6.1.1]--前课复习(1).mp4 (85.97MB).mp4%22%2C%22size%22%3A90144844%2C%22taskId%22%3A%22u017e4acf-21fd-48c3-8a4f-39db410b2ae%22%2C%22taskType%22%3A%22upload%22%2C%22url%22%3Anull%2C%22cover%22%3Anull%2C%22videoId%22%3A%22inputs%2Fprod%2Fyuque%2F2023%2F2331396%2Fmp4%2F1688480390021-10cc712e-a454-480a-813e-e785d50d9717.mp4%22%2C%22download%22%3Afalse%2C%22__spacing%22%3A%22both%22%2C%22id%22%3A%22G7G1H%22%2C%22margin%22%3A%7B%22top%22%3Atrue%2C%22bottom%22%3Atrue%7D%2C%22card%22%3A%22video%22%7D#G7G1H)

本课概要

[6.1.2]--本课概要(1).mp4 (35.5MB).mp4%22%2C%22size%22%3A37227294%2C%22taskId%22%3A%22u66ff1154-1024-4601-aef3-ba96235c124%22%2C%22taskType%22%3A%22upload%22%2C%22url%22%3Anull%2C%22cover%22%3Anull%2C%22videoId%22%3A%22inputs%2Fprod%2Fyuque%2F2023%2F2331396%2Fmp4%2F1688480397500-6f0912d4-04ab-4109-8d11-c1179f6e7738.mp4%22%2C%22download%22%3Afalse%2C%22__spacing%22%3A%22both%22%2C%22id%22%3A%22nYMk1%22%2C%22margin%22%3A%7B%22top%22%3Atrue%2C%22bottom%22%3Atrue%7D%2C%22card%22%3A%22video%22%7D#nYMk1)

函数的定义与使用

单元开篇

[6.2.1]--单元开篇(1).mp4 (13.45MB).mp4%22%2C%22size%22%3A14106042%2C%22taskId%22%3A%22u0a96ae3e-8cb9-426c-baa4-6e5d98d74cf%22%2C%22taskType%22%3A%22upload%22%2C%22url%22%3Anull%2C%22cover%22%3Anull%2C%22videoId%22%3A%22inputs%2Fprod%2Fyuque%2F2023%2F2331396%2Fmp4%2F1688480367029-059a1b72-e61c-48d5-8bb6-332da6cdb0b0.mp4%22%2C%22download%22%3Afalse%2C%22__spacing%22%3A%22both%22%2C%22id%22%3A%22KbRE7%22%2C%22margin%22%3A%7B%22top%22%3Atrue%2C%22bottom%22%3Atrue%7D%2C%22card%22%3A%22video%22%7D#KbRE7)

函数的理解与定义

[6.2.2]--函数的理解和定义(1).mp4 (51.27MB).mp4%22%2C%22size%22%3A53762333%2C%22taskId%22%3A%22ub01094ba-3ef3-4748-94b1-da875422d05%22%2C%22taskType%22%3A%22upload%22%2C%22url%22%3Anull%2C%22cover%22%3Anull%2C%22videoId%22%3A%22inputs%2Fprod%2Fyuque%2F2023%2F2331396%2Fmp4%2F1688480367030-dc59a76a-8be4-4238-852a-297df5010349.mp4%22%2C%22download%22%3Afalse%2C%22__spacing%22%3A%22both%22%2C%22id%22%3A%22YxIHF%22%2C%22margin%22%3A%7B%22top%22%3Atrue%2C%22bottom%22%3Atrue%7D%2C%22card%22%3A%22video%22%7D#YxIHF)

  • 函数是一段具有特定功能的、可重用的语句组
  • 函数是一种功能的抽象，一般函数表达特定功能
  • 函数的两个主要作用：
    • 降低编程难度
    • 代码复用
  • 函数定义时，所指定的参数是一种占位符
  • 函数定义后，如果不经过调用，不会被执行
  • 函数定义时，参数是输入、函数体是处理、结果是输出（IPO）
  1. def dayUP(df):
  2.     dayup = 1
  3.     for i in range(365):
  4.         if i % 7 in [6, 0]:
  5.             dayup = dayup * (1 - 0.01)
  6.         else:
  7.             dayup = dayup * (1 + df)
  8.     return dayup
  11. dayfactor = 0.01
  12. while dayUP(dayfactor) < 37.78: # 37.78 是一年每天努力 1% 的结果
  13.     dayfactor += 0.001
  14. print("工作日的努力参数是：{:.3f} ".format(dayfactor))
  15. # 工作日的努力参数是：0.019

Python 函数的书写格式：
image.png

image.png

  1. def fact(n):
  2.     s = 1
  3.     for i in range(1, n + 1):
  4.         s *= i
  5.     return s
  • 函数名：fact
  • 函数参数：n
  • 函数返回值：s

函数的使用及调用过程

[6.2.3]--函数的使用及调用过程(1).mp4 (33.79MB).mp4%22%2C%22size%22%3A35434263%2C%22taskId%22%3A%22u86453745-1c95-42af-9a45-e6874bb7c96%22%2C%22taskType%22%3A%22upload%22%2C%22url%22%3Anull%2C%22cover%22%3Anull%2C%22videoId%22%3A%22inputs%2Fprod%2Fyuque%2F2023%2F2331396%2Fmp4%2F1688480367046-dad3b13a-9069-4d4f-9d63-43f36bdca499.mp4%22%2C%22download%22%3Afalse%2C%22__spacing%22%3A%22both%22%2C%22id%22%3A%22Ugdw6%22%2C%22margin%22%3A%7B%22top%22%3Atrue%2C%22bottom%22%3Atrue%7D%2C%22card%22%3A%22video%22%7D#Ugdw6) 调用是运行函数代码的方式

image.png

函数的调用过程：（图中的箭头是动态一步步生成的，若不清楚函数的调用过程，建议回看视频以了解详细步骤）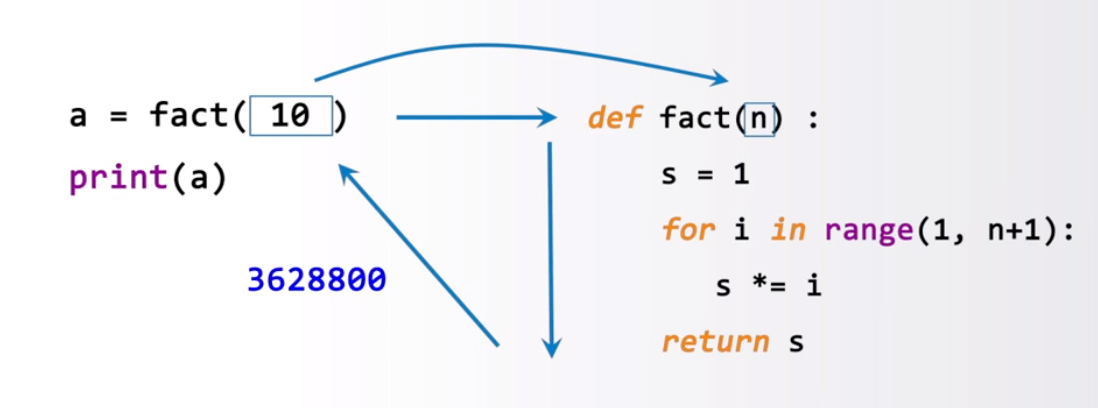
image.png

  1. def fact(n):
  2.     s = 1
  3.     for i in range(1, n + 1):
  4.         s *= i
  5.     return s
  8. a = fact(10)
  10. print(a) # 3628800

函数的参数传递

[6.2.4]--函数的参数传递(1).mp4 (85.59MB).mp4%22%2C%22size%22%3A89750489%2C%22taskId%22%3A%22u249239ed-04e9-49bc-b21e-79ef7026d74%22%2C%22taskType%22%3A%22upload%22%2C%22url%22%3Anull%2C%22cover%22%3Anull%2C%22videoId%22%3A%22inputs%2Fprod%2Fyuque%2F2023%2F2331396%2Fmp4%2F1688480367053-1aef95cd-3a39-4249-af24-daffbc2b0aed.mp4%22%2C%22download%22%3Afalse%2C%22__spacing%22%3A%22both%22%2C%22id%22%3A%22IhIEL%22%2C%22margin%22%3A%7B%22top%22%3Atrue%2C%22bottom%22%3Atrue%7D%2C%22card%22%3A%22video%22%7D#IhIEL) image.png

可选参数：
image.png

image.png

  1. def fact(n, m=1): # 可选参数、参数默认值
  2.     s = 1
  3.     for i in range(1, n + 1):
  4.         s *= i
  5.     return s // m
  8. print(fact(10))  # 3628800
  9. print(fact(10, 5))  # 725760

可变参数：
image.png
image.png

  1. def fact(n, *b): # 可变参数
  2.     s = 1
  3.     for i in range(1, n + 1):
  4.         s *= i
  5.     for item in b:
  6.         s *= item
  7.     return s
  10. print(fact(10, 3))  # 10886400
  11. print(fact(10, 3, 5, 8))  # 435456000

image.png

  1. def fact(n, m=1):
  2.     s = 1
  3.     for i in range(1, n + 1):
  4.         s *= i
  5.     return s // m
  8. # 传参：位置传递
  9. print(fact(10, 5))  # 725760
  10. # 传参：名称传递
  11. print(fact(m=5, n=10))  # 725760

函数的返回值

[6.2.5]--函数的返回值(1).mp4 (31.92MB).mp4%22%2C%22size%22%3A33471487%2C%22taskId%22%3A%22u6b842606-70e2-4a39-9117-452e63b0f9f%22%2C%22taskType%22%3A%22upload%22%2C%22url%22%3Anull%2C%22cover%22%3Anull%2C%22videoId%22%3A%22inputs%2Fprod%2Fyuque%2F2023%2F2331396%2Fmp4%2F1688480367053-9d6589eb-62ea-4185-b23d-2257624f46c1.mp4%22%2C%22download%22%3Afalse%2C%22__spacing%22%3A%22both%22%2C%22id%22%3A%22PynA4%22%2C%22margin%22%3A%7B%22top%22%3Atrue%2C%22bottom%22%3Atrue%7D%2C%22card%22%3A%22video%22%7D#PynA4) image.png
image.png

  1. def fact(n, m=1):
  2.     s = 1
  3.     for i in range(1, n + 1):
  4.         s *= i
  5.     return s // m, n, m # 返回多个结果
  8. print(fact(10, 5))  # (725760, 10, 5)
  9. # 返回结果 (725760, 10, 5) 是一个 元组类型
  11. # 定义变量接收返回结果
  12. a, b, c = fact(10, 5)
  13. print(a, b, c) # 725760 10 5

局部变量和全局变量

[6.2.6]--局部变量和全局变量(1).mp4 (142.13MB).mp4%22%2C%22size%22%3A149031881%2C%22taskId%22%3A%22u0da483f9-1e09-404b-aba9-e8bd6fd8e66%22%2C%22taskType%22%3A%22upload%22%2C%22url%22%3Anull%2C%22cover%22%3Anull%2C%22videoId%22%3A%22inputs%2Fprod%2Fyuque%2F2023%2F2331396%2Fmp4%2F1688480377688-c2a6b4d6-0d4f-46ec-a55a-bcfdd4634920.mp4%22%2C%22download%22%3Afalse%2C%22__spacing%22%3A%22both%22%2C%22id%22%3A%22wAyKl%22%2C%22margin%22%3A%7B%22top%22%3Atrue%2C%22bottom%22%3Atrue%7D%2C%22card%22%3A%22video%22%7D#wAyKl) image.png

image.png

  1. n, s = 10, 100  # n 和 s 是全局变量
  4. def fact(n):  # fact() 函数中的 n 和 s 是局部变量
  5.     s = 1
  6.     for i in range(1, n + 1):
  7.         s *= i
  8.     return s
  11. # 访问到的是全局变量 n 10 s 100
  12. print(fact(n), s) # 3628800 100

规则1：局部变量和全局变量是不同变量

  • 局部变量是函数内部的占位符，与全局变量可能重名但不同
  • 函数运算结束后，局部变量被释放
  • 可以使用 global 保留字在函数内部使用全局变量

image.png

image.png

  1. n, s = 10, 100
  4. def fact(n):
  5.     # s = 1 # 局部变量
  6.     global s  # 使用全局变量 s
  7.     for i in range(1, n + 1):
  8.         s *= i
  9.     return s
  12. print(fact(n), s)  # 362880000 362880000

规则2：局部变量为组合数据类型且未创建，等同于全局变量

image.png

  1. ls = ["F", "f"]
  4. def func(a):
  5.     ls.append(a)
  6.     return
  9. func("C")
  10. print(ls)  # ['F', 'f', 'C']

image.png

  1. ls = ["F", "f"]
  4. def func(a):
  5.     ls = []
  6.     ls.append(a)
  7.     print(ls) # ['C']
  8.     return
  11. func("C")
  12. print(ls)  # ['F', 'f']

小结：

  • 基本数据类型，无论是否重名，局部变量与全局变量不同
  • 可以通过global保留字在函数内部声明全局变量
  • 组合数据类型，如果局部变量未真实创建，则是全局变量

lambda 函数

[6.2.7]--lambda函数(1).mp4 (47.76MB).mp4%22%2C%22size%22%3A50075390%2C%22taskId%22%3A%22u2b100a0e-ad7f-45ad-b612-2cd6ed363cf%22%2C%22taskType%22%3A%22upload%22%2C%22url%22%3Anull%2C%22cover%22%3Anull%2C%22videoId%22%3A%22inputs%2Fprod%2Fyuque%2F2023%2F2331396%2Fmp4%2F1688480383338-a201d019-2a15-445c-8698-c677828fcd3c.mp4%22%2C%22download%22%3Afalse%2C%22__spacing%22%3A%22both%22%2C%22id%22%3A%22DIGIn%22%2C%22margin%22%3A%7B%22top%22%3Atrue%2C%22bottom%22%3Atrue%7D%2C%22card%22%3A%22video%22%7D#DIGIn) lambda 函数返回函数名作为结果

  • lambda 函数是一种匿名函数，即没有名字的函数
  • 使用 lambda 保留字定义，函数名是返回结果
  • lambda 函数用于定义简单的、能够在一行内表示的函数
  1. f = lambda x, y: x + y
  2. print(f(10, 15)) # 25
  1. f = lambda: "lambda函数"
  2. print(f()) # lambda函数

谨慎使用 lambda 函数:

  • lambda 函数主要用作一些特定函数或方法的参数
  • lambda 函数有一些固定使用方式，建议逐步掌握
  • 一般情况，建议使用 def 定义的普通函数

单元小结

[6.2.8]--单元小结(1).mp4 (22.23MB).mp4%22%2C%22size%22%3A23313968%2C%22taskId%22%3A%22ude9681d3-d3e5-4449-aa88-416bc157226%22%2C%22taskType%22%3A%22upload%22%2C%22url%22%3Anull%2C%22cover%22%3Anull%2C%22videoId%22%3A%22inputs%2Fprod%2Fyuque%2F2023%2F2331396%2Fmp4%2F1688480383492-0ee6c95b-4c8f-4a1a-bc6c-36171ed0320d.mp4%22%2C%22download%22%3Afalse%2C%22__spacing%22%3A%22both%22%2C%22id%22%3A%22O4Ebd%22%2C%22margin%22%3A%7B%22top%22%3Atrue%2C%22bottom%22%3Atrue%7D%2C%22card%22%3A%22video%22%7D#O4Ebd)

  • 使用保留字def定义函数，lambda定义匿名函数
  • 可选参数(赋初值)、可变参数(*b)、名称传递
  • 保留字return可以返回任意多个结果
  • 保留字global声明使用全局变量，一些隐式规则

实例 7: 七段数码管绘制

问题分析

[6.3.1]--七段数码管绘制问题分析(1).mp4 (31.05MB).mp4%22%2C%22size%22%3A32556812%2C%22taskId%22%3A%22u82e6411a-f30a-4eee-a359-fc653f7a927%22%2C%22taskType%22%3A%22upload%22%2C%22url%22%3Anull%2C%22cover%22%3Anull%2C%22videoId%22%3A%22inputs%2Fprod%2Fyuque%2F2023%2F2331396%2Fmp4%2F1688480427560-908d1056-4926-476d-af45-2390113e7700.mp4%22%2C%22download%22%3Afalse%2C%22__spacing%22%3A%22both%22%2C%22id%22%3A%22BUg2l%22%2C%22margin%22%3A%7B%22top%22%3Atrue%2C%22bottom%22%3Atrue%7D%2C%22card%22%3A%22video%22%7D#BUg2l)

实例讲解（上）

[6.3.2]--七段数码管绘制实例讲解(上)(1).mp4 (192.94MB)(1).mp4%22%2C%22size%22%3A202312768%2C%22taskId%22%3A%22u62994d3f-a846-4c83-a49d-21ca26dbc20%22%2C%22taskType%22%3A%22upload%22%2C%22url%22%3Anull%2C%22cover%22%3Anull%2C%22videoId%22%3A%22inputs%2Fprod%2Fyuque%2F2023%2F2331396%2Fmp4%2F1688480427569-f95ed643-3ebb-483c-8841-cc0a2d424e99.mp4%22%2C%22download%22%3Afalse%2C%22__spacing%22%3A%22both%22%2C%22id%22%3A%22Xogip%22%2C%22margin%22%3A%7B%22top%22%3Atrue%2C%22bottom%22%3Atrue%7D%2C%22card%22%3A%22video%22%7D#Xogip) 基本思路：

  • 步骤1：绘制单个数字对应的数码管
  • 步骤2：获得一串数字，绘制对应的数码管
  • 步骤3：获得当前系统时间，绘制对应的数码管

image.png

  1. import turtle
  4. def drawLine(draw):  # 绘制单段数码管
  5.     turtle.pendown() if draw else turtle.penup()
  6.     turtle.fd(40)
  7.     turtle.right(90)
  10. def drawDigit(digit):  # 根据数字绘制七段数码管
  11.     drawLine(True) if digit in [2, 3, 4, 5, 6, 8, 9] else drawLine(False)
  12.     drawLine(True) if digit in [0, 1, 3, 4, 5, 6, 7, 8, 9] else drawLine(False)
  13.     drawLine(True) if digit in [0, 2, 3, 5, 6, 8, 9] else drawLine(False)
  14.     drawLine(True) if digit in [0, 2, 6, 8] else drawLine(False)
  15.     turtle.left(90)
  16.     drawLine(True) if digit in [0, 4, 5, 6, 8, 9] else drawLine(False)
  17.     drawLine(True) if digit in [0, 2, 3, 5, 6, 7, 8, 9] else drawLine(False)
  18.     drawLine(True) if digit in [0, 1, 2, 3, 4, 7, 8, 9] else drawLine(False)
  19.     turtle.left(180)
  20.     turtle.penup()
  21.     turtle.fd(20)
  24. def drawDate(date):  # 获得要输出的数字
  25.     for i in date:
  26.         drawDigit(eval(i))  # 通过eval()函数将数字变为整数
  29. def main():
  30.     turtle.setup(800, 350, 200, 200)
  31.     turtle.penup()
  32.     turtle.fd(-300)
  33.     turtle.pensize(5)
  34.     drawDate("20181010")
  35.     turtle.hideturtle()
  36.     turtle.done()
  39. main()

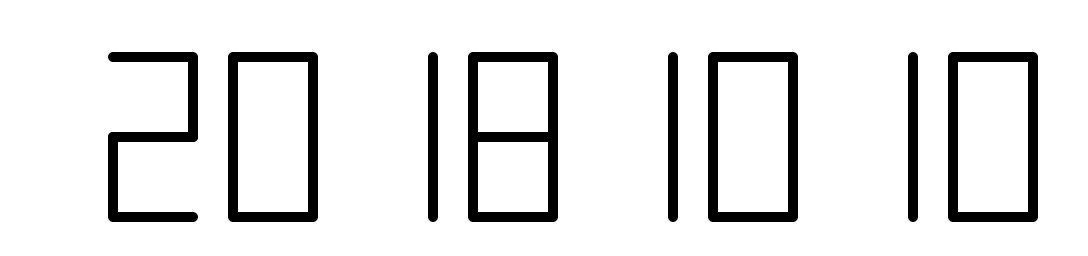
image.png

实例讲解（下）

[6.3.3]--七段数码管绘制实例讲解(下)(1).mp4 (148.16MB)(1).mp4%22%2C%22size%22%3A155357059%2C%22taskId%22%3A%22uc9bbee43-4c98-4e17-8a76-9a7dcfd77e5%22%2C%22taskType%22%3A%22upload%22%2C%22url%22%3Anull%2C%22cover%22%3Anull%2C%22videoId%22%3A%22inputs%2Fprod%2Fyuque%2F2023%2F2331396%2Fmp4%2F1688480427591-ff965b43-d5c0-4172-b0cf-2d9ea0f72ad3.mp4%22%2C%22download%22%3Afalse%2C%22__spacing%22%3A%22both%22%2C%22id%22%3A%22MiRuK%22%2C%22margin%22%3A%7B%22top%22%3Atrue%2C%22bottom%22%3Atrue%7D%2C%22card%22%3A%22video%22%7D#MiRuK)

  1. import turtle, time
  4. def drawGap():  # 绘制数码管间隔
  5.     turtle.penup()
  6.     turtle.fd(5)
  9. def drawLine(draw):  # 绘制单段数码管
  10.     drawGap()
  11.     turtle.pendown() if draw else turtle.penup()
  12.     turtle.fd(40)
  13.     drawGap()
  14.     turtle.right(90)
  17. def drawDigit(d):  # 根据数字绘制七段数码管
  18.     drawLine(True) if d in [2, 3, 4, 5, 6, 8, 9] else drawLine(False)
  19.     drawLine(True) if d in [0, 1, 3, 4, 5, 6, 7, 8, 9] else drawLine(False)
  20.     drawLine(True) if d in [0, 2, 3, 5, 6, 8, 9] else drawLine(False)
  21.     drawLine(True) if d in [0, 2, 6, 8] else drawLine(False)
  22.     turtle.left(90)
  23.     drawLine(True) if d in [0, 4, 5, 6, 8, 9] else drawLine(False)
  24.     drawLine(True) if d in [0, 2, 3, 5, 6, 7, 8, 9] else drawLine(False)
  25.     drawLine(True) if d in [0, 1, 2, 3, 4, 7, 8, 9] else drawLine(False)
  26.     turtle.left(180)
  27.     turtle.penup()
  28.     turtle.fd(20)
  31. def drawDate(date):
  32.     turtle.pencolor("red")
  33.     for i in date:
  34.         if i == "-":
  35.             turtle.write("年", font=("Arial", 18, "normal"))
  36.             turtle.pencolor("green")
  37.             turtle.fd(40)
  38.         elif i == "=":
  39.             turtle.write("月", font=("Arial", 18, "normal"))
  40.             turtle.pencolor("blue")
  41.             turtle.fd(40)
  42.         elif i == "+":
  43.             turtle.write("日", font=("Arial", 18, "normal"))
  44.         else:
  45.             drawDigit(eval(i))
  48. def main():
  49.     turtle.setup(800, 350, 200, 200)
  50.     turtle.penup()
  51.     turtle.fd(-350)
  52.     turtle.pensize(5)
  53.     #    drawDate('2018-10=10+')
  54.     drawDate(time.strftime("%Y-%m=%d+", time.gmtime()))
  55.     turtle.hideturtle()
  56.     turtle.done()
  59. main()

image.png

举一反三

[6.3.4]--七段数码管绘制举一反三(1).mp4 (54.51MB).mp4%22%2C%22size%22%3A57162767%2C%22taskId%22%3A%22uc8e13a9f-5aa6-4974-b4f6-5883585fed6%22%2C%22taskType%22%3A%22upload%22%2C%22url%22%3Anull%2C%22cover%22%3Anull%2C%22videoId%22%3A%22inputs%2Fprod%2Fyuque%2F2023%2F2331396%2Fmp4%2F1688480427587-d2ef7272-47c5-4121-8fef-93f58c1e0839.mp4%22%2C%22download%22%3Afalse%2C%22__spacing%22%3A%22both%22%2C%22id%22%3A%22nOLRg%22%2C%22margin%22%3A%7B%22top%22%3Atrue%2C%22bottom%22%3Atrue%7D%2C%22card%22%3A%22video%22%7D#nOLRg) 理解方法思维

  • 模块化思维：确定模块接口，封装功能
  • 规则化思维：抽象过程为规则，计算机自动执行
  • 化繁为简：将大功能变为小功能组合，分而治之

image.png

代码复用与函数递归

单元开篇

[6.4.1]--单元开篇(1).mp4 (10.18MB).mp4%22%2C%22size%22%3A10672531%2C%22taskId%22%3A%22u430c691c-72bb-4d8d-abf7-2ae059238e1%22%2C%22taskType%22%3A%22upload%22%2C%22url%22%3Anull%2C%22cover%22%3Anull%2C%22videoId%22%3A%22inputs%2Fprod%2Fyuque%2F2023%2F2331396%2Fmp4%2F1688480440724-5f80e90d-994d-41e1-98ff-81f33f9ef97c.mp4%22%2C%22download%22%3Afalse%2C%22__spacing%22%3A%22both%22%2C%22id%22%3A%22EbmGa%22%2C%22margin%22%3A%7B%22top%22%3Atrue%2C%22bottom%22%3Atrue%7D%2C%22card%22%3A%22video%22%7D#EbmGa)

代码复用与模块化设计

[6.4.2]--代码复用与模块化设计(1).mp4 (100.83MB).mp4%22%2C%22size%22%3A105728177%2C%22taskId%22%3A%22uad27252e-7b85-4b33-9582-16fb9ebca51%22%2C%22taskType%22%3A%22upload%22%2C%22url%22%3Anull%2C%22cover%22%3Anull%2C%22videoId%22%3A%22inputs%2Fprod%2Fyuque%2F2023%2F2331396%2Fmp4%2F1688480441437-1ba4a3cb-34b3-43e0-a3e8-35c6dc11c148.mp4%22%2C%22download%22%3Afalse%2C%22__spacing%22%3A%22both%22%2C%22id%22%3A%22uZe0l%22%2C%22margin%22%3A%7B%22top%22%3Atrue%2C%22bottom%22%3Atrue%7D%2C%22card%22%3A%22video%22%7D#uZe0l) 代码复用：把代码当成资源进行抽象

  • 代码资源化：程序代码是一种用来表达计算的”资源”
  • 代码抽象化：使用函数等方法对代码赋予更高级别的定义
  • 代码复用：同一份代码在需要时可以被重复使用

函数 和 对象 是代码复用的两种主要形式

image.png

模块化设计：分而治之

  • 通过函数或对象封装将程序划分为模块及模块间的表达
  • 具体包括：主程序、子程序和子程序间关系
  • 分而治之：一种分而治之、分层抽象、体系化的设计思想

模块化设计：紧耦合、松耦合

  • 紧耦合：两个部分之间交流很多，无法独立存在
  • 松耦合：两个部分之间交流较少，可以独立存在
  • 模块内部紧耦合、模块之间松耦合

函数递归的理解

[6.4.3]--函数递归的理解(1).mp4 (44.67MB).mp4%22%2C%22size%22%3A46838195%2C%22taskId%22%3A%22u7150fe42-bdbb-4a3f-805b-0f9595d9fc7%22%2C%22taskType%22%3A%22upload%22%2C%22url%22%3Anull%2C%22cover%22%3Anull%2C%22videoId%22%3A%22inputs%2Fprod%2Fyuque%2F2023%2F2331396%2Fmp4%2F1688480449504-8efd248b-8bb6-4447-82fd-e20401b61100.mp4%22%2C%22download%22%3Afalse%2C%22__spacing%22%3A%22both%22%2C%22id%22%3A%22hlwF3%22%2C%22margin%22%3A%7B%22top%22%3Atrue%2C%22bottom%22%3Atrue%7D%2C%22card%22%3A%22video%22%7D#hlwF3) 递归：函数定义中调用函数自身的方式

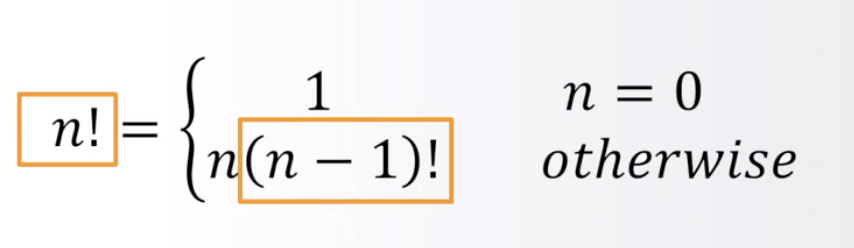
image.png

递归的两个关键特征：

  • 链条：计算过程存在递归链条
  • 基例：存在一个或多个不需要再低递归的基例

    注意读音： image.png

递归类似数学归纳法：

  • 证明当n取第一个值n0时命题成立
  • 假设当nk时命题成立，证明当n=nk+1时命题也成立

递归是数学归纳法思维的编程体现。

函数递归的调用过程

[6.4.4]--函数递归的调用过程(1).mp4 (115.88MB).mp4%22%2C%22size%22%3A121504202%2C%22taskId%22%3A%22u4d3317c4-1b17-4d42-801c-bd8507b0d26%22%2C%22taskType%22%3A%22upload%22%2C%22url%22%3Anull%2C%22cover%22%3Anull%2C%22videoId%22%3A%22inputs%2Fprod%2Fyuque%2F2023%2F2331396%2Fmp4%2F1688480450148-63af4042-2e2f-45d3-a723-b2caf3da550f.mp4%22%2C%22download%22%3Afalse%2C%22__spacing%22%3A%22both%22%2C%22id%22%3A%22XsFGx%22%2C%22margin%22%3A%7B%22top%22%3Atrue%2C%22bottom%22%3Atrue%7D%2C%22card%22%3A%22video%22%7D#XsFGx) image.png

  1. def fact(n):
  2.     if n == 0:
  3.         return 1
  4.     else:
  5.         return n * fact(n - 1)
  8. print(fact(0))  # 1
  9. print(fact(1))  # 1
  10. print(fact(2))  # 2
  11. print(fact(3))  # 6
  12. print(fact(4))  # 24
  13. print(fact(5))  # 120

递归的实现：函数 + 分支语句

  • 递归本身是一个函数，需要函数定义方式描述
  • 函数内部，采用分支语句对输入参数进行判断
  • 基例和链条，分别编写对应代码

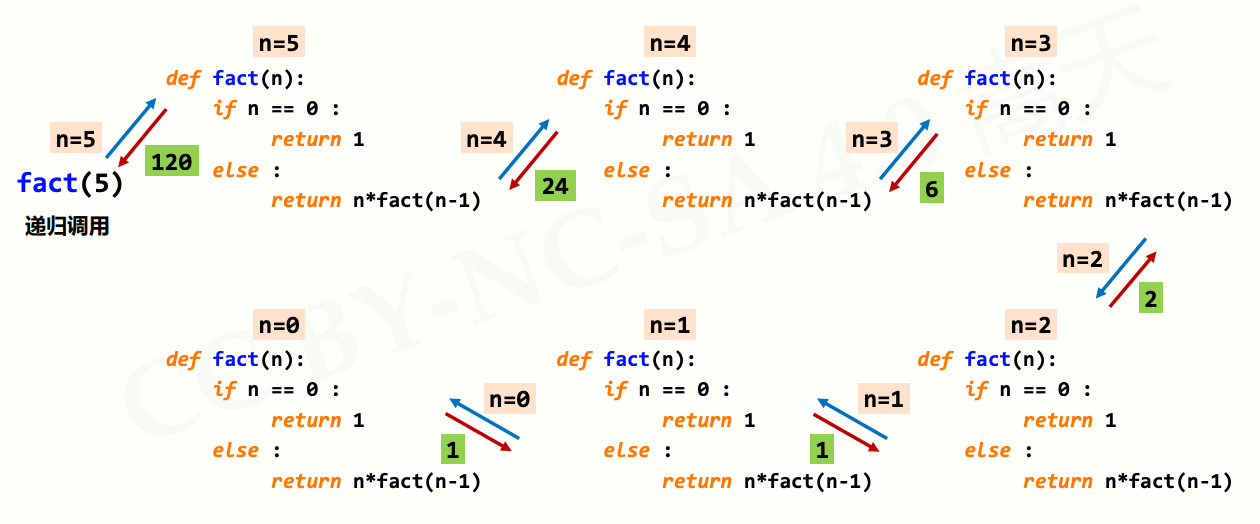
image.png

函数递归实例解析

[6.4.5]--函数递归实例解析(1).mp4 (222.61MB).mp4%22%2C%22size%22%3A233427107%2C%22taskId%22%3A%22ud096b704-cf83-464b-91e7-d0d3b504878%22%2C%22taskType%22%3A%22upload%22%2C%22url%22%3Anull%2C%22cover%22%3Anull%2C%22videoId%22%3A%22inputs%2Fprod%2Fyuque%2F2023%2F2331396%2Fmp4%2F1688480474820-96f261ae-db5b-4747-9048-5a22fdaba457.mp4%22%2C%22download%22%3Afalse%2C%22__spacing%22%3A%22both%22%2C%22id%22%3A%22X2hJn%22%2C%22margin%22%3A%7B%22top%22%3Atrue%2C%22bottom%22%3Atrue%7D%2C%22card%22%3A%22video%22%7D#X2hJn) image.png

  1. def rvs(s):
  2.     if s == "":
  3.         return s
  4.     else:
  5.         return rvs(s[1:]) + s[0]

image.png

5. 函数和代码复用 - 图54

  1. def f(n):
  2.     if n == 1 or n == 2:
  3.         return 1
  4.     else:
  5.         return f(n - 1) + f(n - 2)

image.png

  1. count = 0
  4. def hanoi(n, src, dst, mid):
  5.     global count
  6.     if n == 1:
  7.         print("{}:{} -> {}".format(1, src, dst))
  8.         count += 1
  9.     else:
  10.         hanoi(n - 1, src, mid, dst)
  11.         print("{}:{} -> {}".format(n, src, dst))
  12.         count += 1
  13.         hanoi(n - 1, mid, dst, src)
  16. hanoi(3, 'A', 'B', 'C')
  18. ''' 
  19. 1:A -> B
  20. 2:A -> C
  21. 1:B -> C
  22. 3:A -> B
  23. 1:C -> A
  24. 2:C -> B
  25. 1:A -> B
  26. '''

单元小结

[6.4.6]--单元小结(1).mp4 (20.92MB).mp4%22%2C%22size%22%3A21931894%2C%22taskId%22%3A%22u25fa0f8c-2174-4765-a674-46c950db424%22%2C%22taskType%22%3A%22upload%22%2C%22url%22%3Anull%2C%22cover%22%3Anull%2C%22videoId%22%3A%22inputs%2Fprod%2Fyuque%2F2023%2F2331396%2Fmp4%2F1688480487665-e4e731e6-c188-4697-a28a-6970bc86eca0.mp4%22%2C%22download%22%3Afalse%2C%22__spacing%22%3A%22both%22%2C%22id%22%3A%22mDtRC%22%2C%22margin%22%3A%7B%22top%22%3Atrue%2C%22bottom%22%3Atrue%7D%2C%22card%22%3A%22video%22%7D#mDtRC)

  • 模块化设计：松耦合、紧耦合
  • 函数递归的2个特征：基例和链条
  • 函数递归的实现：函数 + 分支结构

模块 4: PyInstaller 库的使用

PyInstaller 库基本介绍

[6.5.1]--PyInstaller库基本介绍(1).mp4 (44.29MB).mp4%22%2C%22size%22%3A46437275%2C%22taskId%22%3A%22u79240b87-870a-4f48-9184-5f0ac22b740%22%2C%22taskType%22%3A%22upload%22%2C%22url%22%3Anull%2C%22cover%22%3Anull%2C%22videoId%22%3A%22inputs%2Fprod%2Fyuque%2F2023%2F2331396%2Fmp4%2F1688480488813-2f6ca3a6-0cdf-4a5e-a8ef-a4ce1cf622d1.mp4%22%2C%22download%22%3Afalse%2C%22__spacing%22%3A%22both%22%2C%22id%22%3A%22ieDpI%22%2C%22margin%22%3A%7B%22top%22%3Atrue%2C%22bottom%22%3Atrue%7D%2C%22card%22%3A%22video%22%7D#ieDpI)

  • PyInstaller 库的作用：将 **.py** 源代码转换成无需源代码的可执行文件
    image.png
  • PyInstaller 库是第三方库
  • 官方网站：http://www.pyinstaller.org
  • 第三方库：使用前需要额外安装
  • 安装第三方库需要使用 pip 工具
  • PyInstaller 库的安装：pip install pyinstaller、pip3 install pyinstaller
  1. huyouda@HuyoudeMacBook-Pro ~ % pip3 install pyinstaller
  2. Collecting pyinstaller
  3.   Downloading pyinstaller-5.13.0-py3-none-macosx_10_13_universal2.whl (928 kB)
  4.      ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 928.8/928.8 kB 703.5 kB/s eta 0:00:00
  5. Requirement already satisfied: setuptools>=42.0.0 in /Library/Frameworks/Python.framework/Versions/3.11/lib/python3.11/site-packages (from pyinstaller) (65.5.0)
  6. Collecting altgraph (from pyinstaller)
  7.   Downloading altgraph-0.17.3-py2.py3-none-any.whl (21 kB)
  8. Collecting pyinstaller-hooks-contrib>=2021.4 (from pyinstaller)
  9.   Downloading pyinstaller_hooks_contrib-2023.5-py2.py3-none-any.whl (273 kB)
  10.      ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 273.1/273.1 kB 1.8 MB/s eta 0:00:00
  11. Collecting macholib>=1.8 (from pyinstaller)
  12.   Downloading macholib-1.16.2-py2.py3-none-any.whl (38 kB)
  13. Installing collected packages: altgraph, pyinstaller-hooks-contrib, macholib, pyinstaller
  14. Successfully installed altgraph-0.17.3 macholib-1.16.2 pyinstaller-5.13.0 pyinstaller-hooks-contrib-2023.5

PyInstaller 库使用说明

[6.5.2]--PyInstaller库使用说明(1).mp4 (95.16MB).mp4%22%2C%22size%22%3A99779970%2C%22taskId%22%3A%22ua2446aad-4daf-4be0-a25f-bf7bc25f7cf%22%2C%22taskType%22%3A%22upload%22%2C%22url%22%3Anull%2C%22cover%22%3Anull%2C%22videoId%22%3A%22inputs%2Fprod%2Fyuque%2F2023%2F2331396%2Fmp4%2F1688480501343-a1a128ed-de40-4561-b0c8-46f1aca56937.mp4%22%2C%22download%22%3Afalse%2C%22__spacing%22%3A%22both%22%2C%22id%22%3A%22Iu72r%22%2C%22margin%22%3A%7B%22top%22%3Atrue%2C%22bottom%22%3Atrue%7D%2C%22card%22%3A%22video%22%7D#Iu72r) 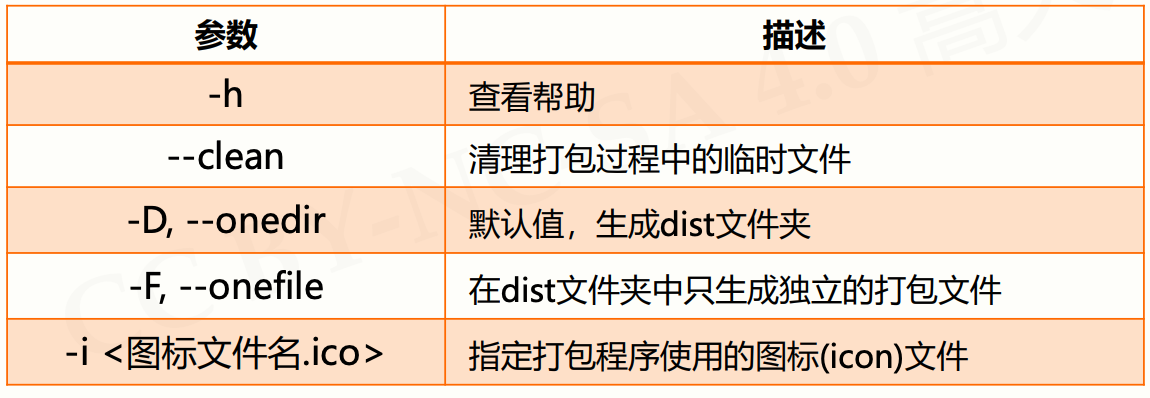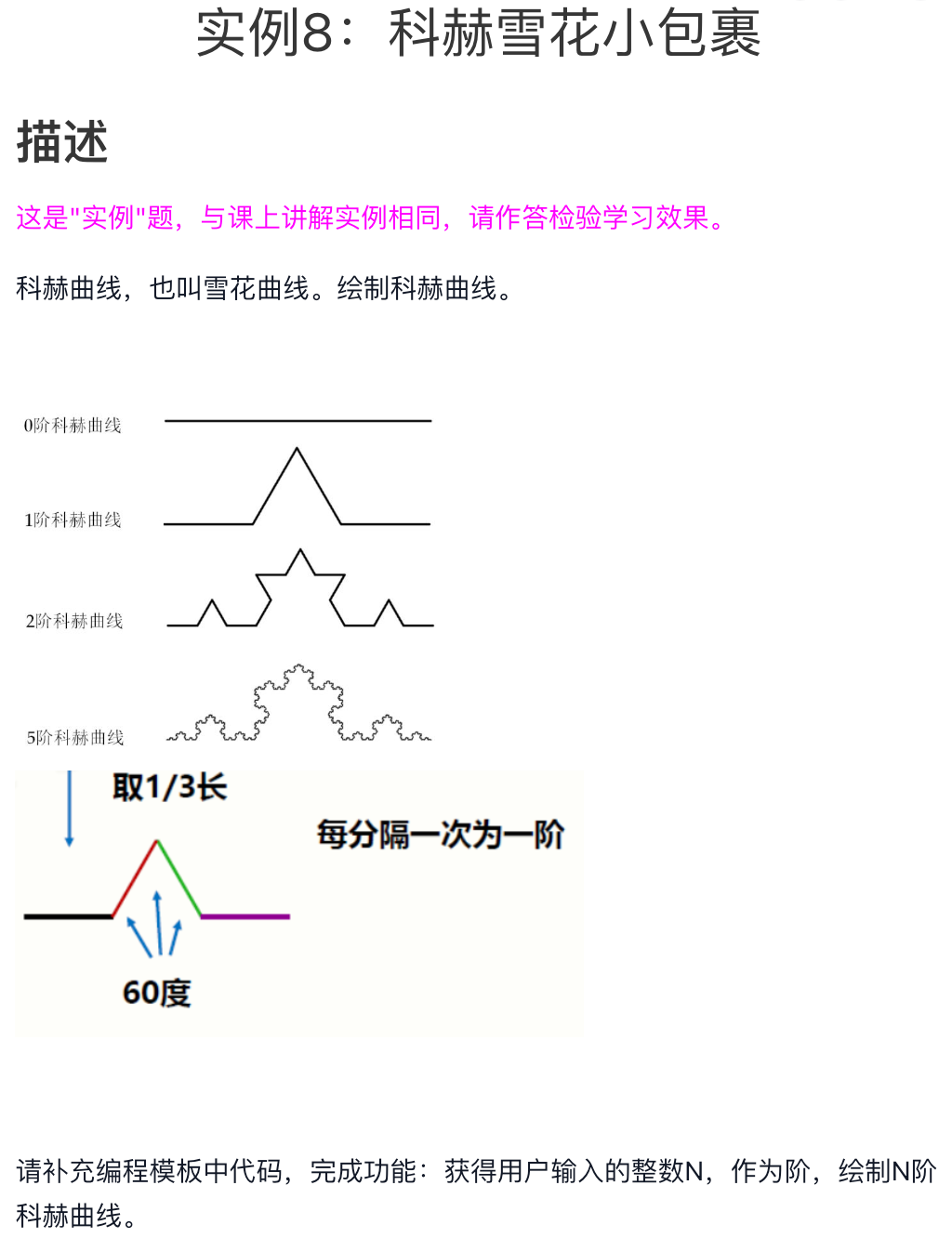image.png

实例 8: 科赫雪花小包裹

问题分析

[6.6.1]--科赫雪花小包裹问题分析(1).mp4 (57.74MB).mp4%22%2C%22size%22%3A60543272%2C%22taskId%22%3A%22ue29c7f29-7211-41cd-84d9-04ad05194bd%22%2C%22taskType%22%3A%22upload%22%2C%22url%22%3Anull%2C%22cover%22%3Anull%2C%22videoId%22%3A%22inputs%2Fprod%2Fyuque%2F2023%2F2331396%2Fmp4%2F1688480502601-b3645403-80c6-43fa-87cc-d92e15e050f2.mp4%22%2C%22download%22%3Afalse%2C%22__spacing%22%3A%22both%22%2C%22id%22%3A%22rO4Z7%22%2C%22margin%22%3A%7B%22top%22%3Atrue%2C%22bottom%22%3Atrue%7D%2C%22card%22%3A%22video%22%7D#rO4Z7)

实例讲解（上）

[6.6.2]--科赫雪花小包裹实例讲解(上)(1).mp4 (107.52MB)(1).mp4%22%2C%22size%22%3A112743253%2C%22taskId%22%3A%22uc7d8148e-a693-4388-b6d2-5214ff6baaa%22%2C%22taskType%22%3A%22upload%22%2C%22url%22%3Anull%2C%22cover%22%3Anull%2C%22videoId%22%3A%22inputs%2Fprod%2Fyuque%2F2023%2F2331396%2Fmp4%2F1688480504481-4a351cd3-5c2b-4058-9e86-de92155d8a38.mp4%22%2C%22download%22%3Afalse%2C%22__spacing%22%3A%22both%22%2C%22id%22%3A%22JMUdt%22%2C%22margin%22%3A%7B%22top%22%3Atrue%2C%22bottom%22%3Atrue%7D%2C%22card%22%3A%22video%22%7D#JMUdt)

  1. import turtle
  4. def koch(size, n):
  5.     if n == 0:
  6.         turtle.fd(size)
  7.     else:
  8.         for angle in [0, 60, -120, 60]:
  9.             turtle.left(angle)
  10.             koch(size / 3, n - 1)
  13. def main():
  14.     turtle.setup(800, 400)
  15.     turtle.penup()
  16.     turtle.goto(-300, -50)
  17.     turtle.pendown()
  18.     turtle.pensize(2)
  19.     koch(600, 3)  # 0阶科赫曲线长度，阶数
  20.     turtle.hideturtle()
  21.     turtle.done()
  24. main()

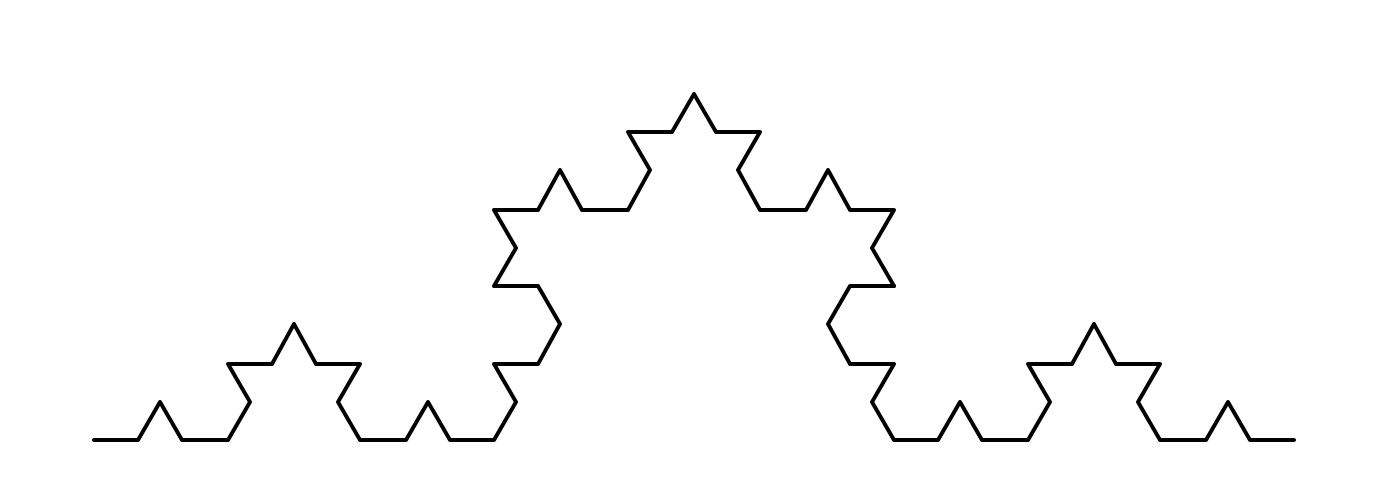
image.png

实例讲解（下）

[6.6.3]--科赫雪花小包裹实例讲解(下)(1).mp4 (36.92MB)(1).mp4%22%2C%22size%22%3A38716633%2C%22taskId%22%3A%22u2bbfdbd6-fb95-4570-a925-765567000ea%22%2C%22taskType%22%3A%22upload%22%2C%22url%22%3Anull%2C%22cover%22%3Anull%2C%22videoId%22%3A%22inputs%2Fprod%2Fyuque%2F2023%2F2331396%2Fmp4%2F1688480510940-cc83ccc9-309b-4f8c-8903-1857f20e77c8.mp4%22%2C%22download%22%3Afalse%2C%22__spacing%22%3A%22both%22%2C%22id%22%3A%22vEdOW%22%2C%22margin%22%3A%7B%22top%22%3Atrue%2C%22bottom%22%3Atrue%7D%2C%22card%22%3A%22video%22%7D#vEdOW)

  1. import turtle
  4. def koch(size, n):
  5.     if n == 0:
  6.         turtle.fd(size)
  7.     else:
  8.         for angle in [0, 60, -120, 60]:
  9.             turtle.left(angle)
  10.             koch(size / 3, n - 1)
  13. def main():
  14.     turtle.setup(600, 600)
  15.     turtle.penup()
  16.     turtle.goto(-200, 100)
  17.     turtle.pendown()
  18.     turtle.pensize(2)
  19.     level = 3  # 3阶科赫雪花，阶数
  20.     koch(400, level)
  21.     turtle.right(120)
  22.     koch(400, level)
  23.     turtle.right(120)
  24.     koch(400, level)
  25.     turtle.hideturtle()
  26.     turtle.done()
  29. main()

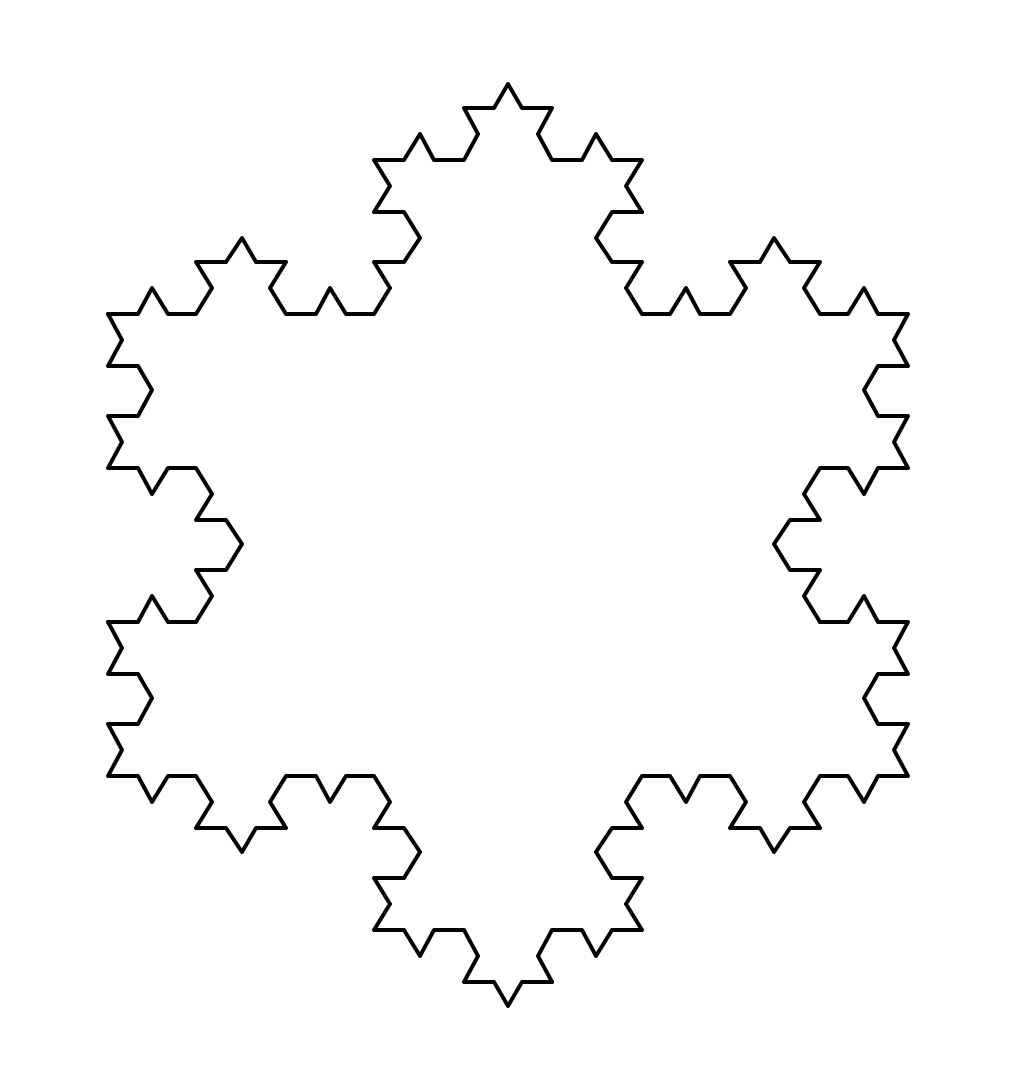
image.png

举一反三

[6.6.4]--科赫雪花小包裹举一反三(1).mp4 (29.13MB).mp4%22%2C%22size%22%3A30542763%2C%22taskId%22%3A%22u92ea7110-1aa3-46e4-9e6a-ea3df913696%22%2C%22taskType%22%3A%22upload%22%2C%22url%22%3Anull%2C%22cover%22%3Anull%2C%22videoId%22%3A%22inputs%2Fprod%2Fyuque%2F2023%2F2331396%2Fmp4%2F1688480531293-4ad1cc9f-8f03-4e0a-9075-6bf5ce638d4a.mp4%22%2C%22download%22%3Afalse%2C%22__spacing%22%3A%22both%22%2C%22id%22%3A%22WkBnW%22%2C%22margin%22%3A%7B%22top%22%3Atrue%2C%22bottom%22%3Atrue%7D%2C%22card%22%3A%22video%22%7D#WkBnW)

练习

[6.7.1]--练习与作业(1).mp4 (8.42MB).mp4%22%2C%22size%22%3A8825295%2C%22taskId%22%3A%22u2db7a52c-8ad2-43f4-988c-aaa0dfdf98f%22%2C%22taskType%22%3A%22upload%22%2C%22url%22%3Anull%2C%22cover%22%3Anull%2C%22videoId%22%3A%22inputs%2Fprod%2Fyuque%2F2023%2F2331396%2Fmp4%2F1688480532470-b974840f-bea7-45e7-90b5-4e54f69779cb.mp4%22%2C%22download%22%3Afalse%2C%22__spacing%22%3A%22both%22%2C%22id%22%3A%22DN7bI%22%2C%22margin%22%3A%7B%22top%22%3Atrue%2C%22bottom%22%3Atrue%7D%2C%22card%22%3A%22video%22%7D#DN7bI)

单选题

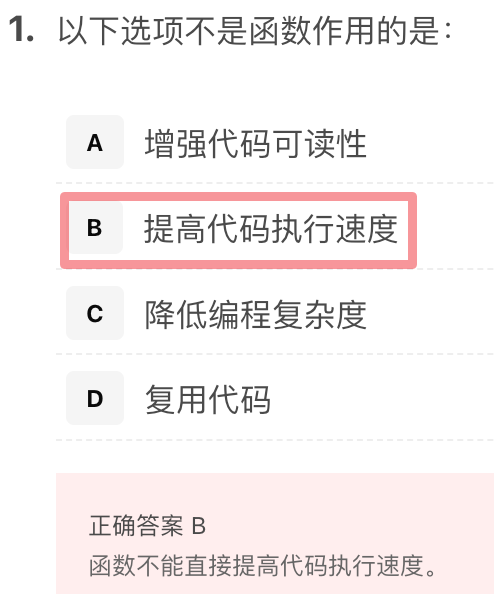
image.png

image.png

  1. def f(a, b):
  2.     a = 4
  3.     return a + b
  6. def main():
  7.     a = 5
  8.     b = 6
  9.     print(f(a, b), a + b)
  12. main() # 10 11

image.png

  1. def func(a, b):
  2.     c = a ** 2 + b
  3.     b = a
  4.     return c
  7. a = 10
  8. b = 100
  9. c = func(a, b) + a
  11. print(a, b, c) # 10 100 210

image.png

image.png

image.png

image.png

image.png

image.png

image.png

连续质数计算

image.png

  1. def prime(m):
  2.     for i in range(2, m):
  3.         if m % i == 0:
  4.             return False
  5.     return True
  8. n = eval(input())
  9. n_ = int(n)
  10. n_ = n_ + 1 if n_ < n else n_
  11. count = 5
  13. while count > 0:
  14.     if prime(n_):
  15.         if count > 1:
  16.             print(n_, end=",")
  17.         else:
  18.             print(n_, end="")
  19.         count -= 1
  20.     n_ += 1
  22. """
  23. 12
  24. 13,17,19,23,29
  25. """

这个代码注意：

(1) 需要对输入小数情况进行判断，获取超过该输入的最小整数（这里没用floor()函数）
(2) 对输出格式进行判断，最后一个输出后不增加逗号（这里没用.join()方法）

实例7：七段数码管绘制

image.png

  1. import turtle as t
  2. import time
  5. def drawGap():  # 绘制数码管间隔
  6.     t.penup()
  7.     t.fd(5)
  10. def drawLine(draw):  # 绘制单段数码管
  11.     drawGap()
  12.     t.pendown() if draw else t.penup()
  13.     t.fd(40)
  14.     drawGap()
  15.     t.right(90)
  18. def drawDigit(d):  # 根据数字绘制七段数码管
  19.     drawLine(True) if d in [2, 3, 4, 5, 6, 8, 9] else drawLine(False)
  20.     drawLine(True) if d in [0, 1, 3, 4, 5, 6, 7, 8, 9] else drawLine(False)
  21.     drawLine(True) if d in [0, 2, 3, 5, 6, 8, 9] else drawLine(False)
  22.     drawLine(True) if d in [0, 2, 6, 8] else drawLine(False)
  23.     t.left(90)
  24.     drawLine(True) if d in [0, 4, 5, 6, 8, 9] else drawLine(False)
  25.     drawLine(True) if d in [0, 2, 3, 5, 6, 7, 8, 9] else drawLine(False)
  26.     drawLine(True) if d in [0, 1, 2, 3, 4, 7, 8, 9] else drawLine(False)
  27.     t.left(180)
  28.     t.penup()
  29.     t.fd(20)
  32. def drawDate(date):
  33.     t.pencolor("red")
  34.     for i in date:
  35.         drawDigit(eval(i))
  38. def main():
  39.     t.setup(800, 350, 200, 200)
  40.     t.penup()
  41.     t.fd(-300)
  42.     t.pensize(5)
  43.     drawDate(time.strftime("%Y%m%d", time.gmtime()))
  44.     t.done()
  47. main()

image.png

这是本课程的实例7：

基本思路：

步骤 1：绘制单个数字对应的码管
步骤 2：获得当前系统时间，变成字符串，绘制对应的码管

思维方法：

  • 模块化思维：确定接口，封装功能
  • 规则化思维：抽象过程为规则，计算机自动执行
  • 化繁为简：将大功能变小组合，分而治之

实例8：科赫雪花小包裹

image.png

  1. import turtle
  4. def koch(size, n):
  5.     if n == 0:
  6.         turtle.fd(size)
  7.     else:
  8.         for angle in [0, 60, -120, 60]:
  9.             turtle.left(angle)
  10.             koch(size / 3, n - 1)
  13. def main(level):
  14.     turtle.setup(600, 600)
  15.     turtle.penup()
  16.     turtle.goto(-200, 100)
  17.     turtle.pendown()
  18.     turtle.pensize(2)
  19.     koch(400, level)
  20.     turtle.right(120)
  21.     koch(400, level)
  22.     turtle.right(120)
  23.     koch(400, level)
  24.     turtle.hideturtle()
  27. try:
  28.     level = eval(input("请输入科赫曲线的阶: "))
  29.     main(level)
  30. except:
  31.     print("输入错误")
  1. import turtle
  4. def koch(size, n):
  5.     if n == 0:
  6.         turtle.fd(size)
  7.     else:
  8.         for angle in [0, 60, -120, 60]:
  9.             turtle.left(angle)
  10.             koch(size / 3, n - 1)
  13. def main(level):
  14.     turtle.setup(600, 600)
  15.     turtle.penup()
  16.     turtle.goto(-200, 100)
  17.     turtle.pendown()
  18.     turtle.pensize(2)
  19.     turtle.speed("fastest")  # 设置绘图速度为最快
  20.     turtle.tracer(100)  # 每100次绘图操作更新一次屏幕
  21.     koch(400, level)
  22.     turtle.right(120)
  23.     koch(400, level)
  24.     turtle.right(120)
  25.     koch(400, level)
  26.     turtle.hideturtle()
  27.     turtle.update()  # 在绘图结束后更新屏幕
  28.     turtle.done() # 绘图完毕后不要自动关闭窗口
  31. try:
  32.     level = eval(input("请输入科赫曲线的阶: "))
  33.     main(level)
  34. except:
  35.     print("输入错误")

请输入科赫曲线的阶: 3
请输入科赫曲线的阶: 4
请输入科赫曲线的阶: 5
请输入科赫曲线的阶: 6

这是本课程的实例8：

(1) 基本思路:

  • 递归思想：函数 +分支
  • 递归链条：线段的组合
  • 递归基例：初始线段

(2) 分形几何是一种迭代的图，广泛存在于自然界中，请尝试选择一个新曲线绘制:

  • 康托尔集、谢宾斯基三角形门格海绵 …
  • 龙形曲线 、空间填充科赫…
  • 函数递归的深入应用 …

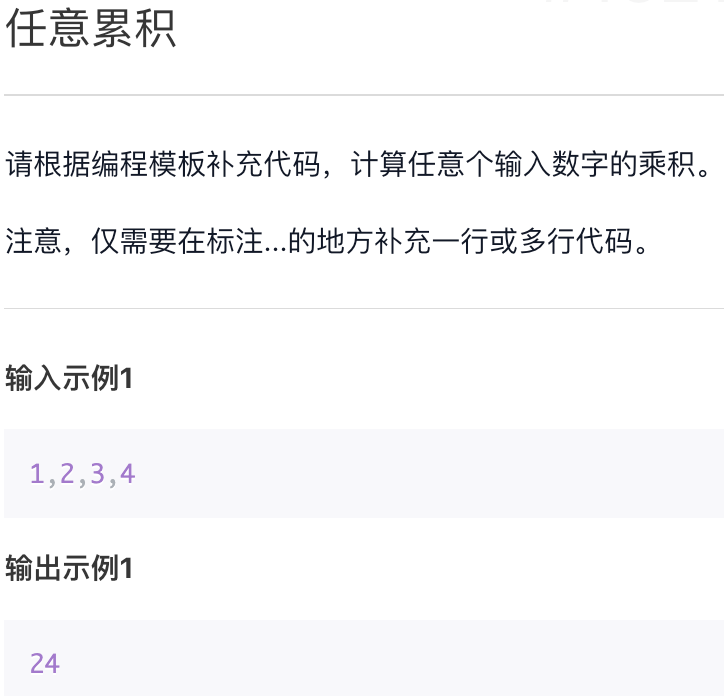
image.png
image.png
image.png
image.png

任意累积

image.png

  1. def cmul(a, *b):
  2.     m = a
  3.     for i in b:
  4.         m *= i
  5.     return m
  8. print(eval("cmul({})".format(input())))
  10. """
  11. 1,2,3,4
  12. 24
  13. """

该程序需要注意两个内容：

  1. 无限制参数数量函数定义的方法，其中 b 在函数 cmul 中表达除了 a 之外的所有输入参数
  2. 以字符串形式调用函数的方法，”cmul()” 与 eval() 的组合，提供了很多灵活性

斐波那契数列计算

image.png

  1. def fbi(n):
  2.     if n == 1 or n == 2:
  3.         return 1
  4.     else:
  5.         return fbi(n - 1) + fbi(n - 2)
  8. n = eval(input())
  9. print(fbi(n))
  11. """
  12. 4
  13. 3
  14. """

基本的递归使用，不解释。

汉诺塔实践

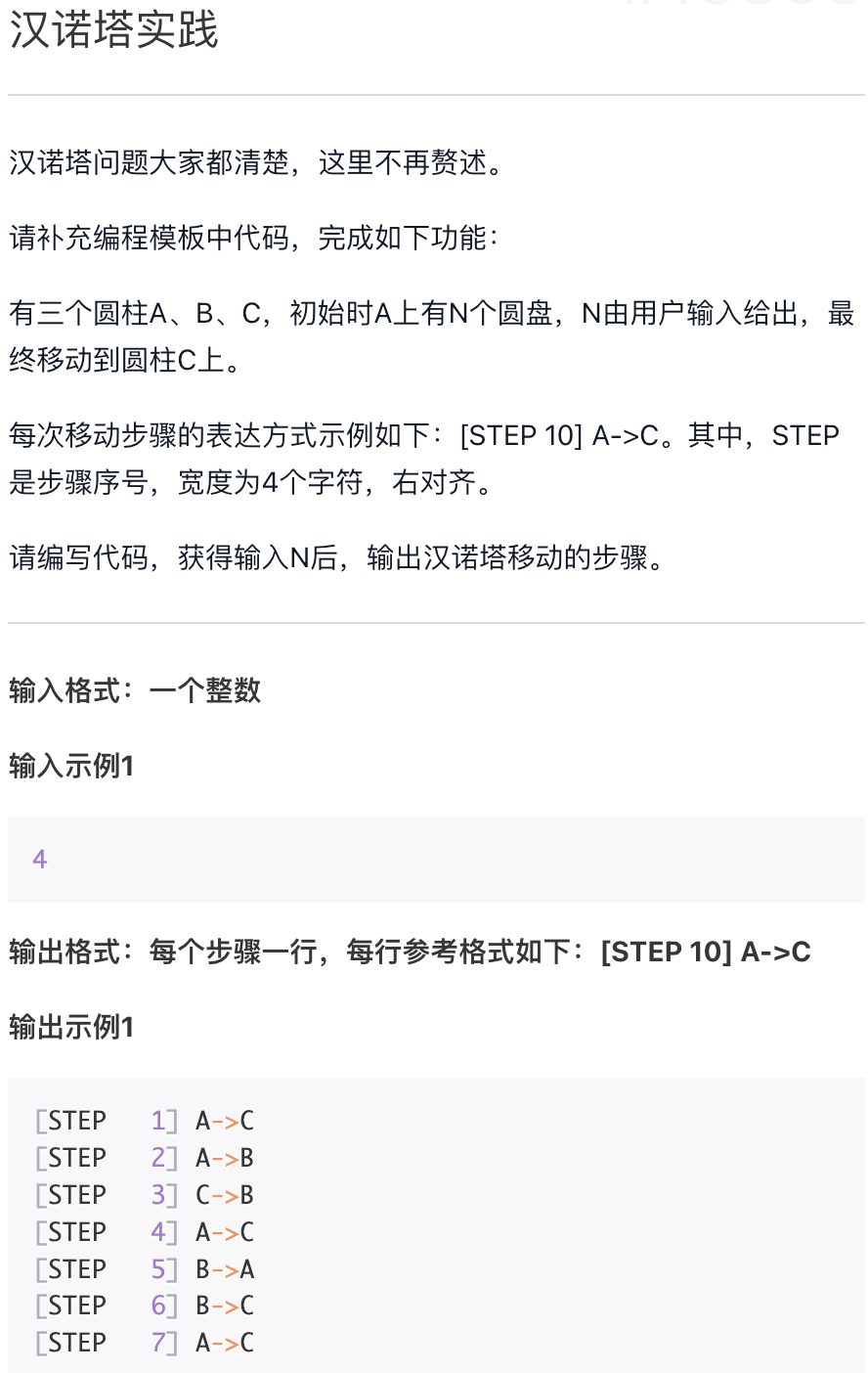
image.png

  1. steps = 0
  4. def hanoi(src, des, mid, n):
  5.     global steps
  6.     if n == 1:
  7.         steps += 1
  8.         print("[STEP{:>4}] {}->{}".format(steps, src, des))
  9.     else:
  10.         hanoi(src, mid, des, n - 1)
  11.         steps += 1
  12.         print("[STEP{:>4}] {}->{}".format(steps, src, des))
  13.         hanoi(mid, des, src, n - 1)
  16. N = eval(input())
  17. hanoi("A", "C", "B", N)
  19. """
  20. 4
  21. [STEP   1] A->B
  22. [STEP   2] A->C
  23. [STEP   3] B->C
  24. [STEP   4] A->B
  25. [STEP   5] C->A
  26. [STEP   6] C->B
  27. [STEP   7] A->B
  28. [STEP   8] A->C
  29. [STEP   9] B->C
  30. [STEP  10] B->A
  31. [STEP  11] C->A
  32. [STEP  12] B->C
  33. [STEP  13] A->B
  34. [STEP  14] A->C
  35. [STEP  15] B->C
  36. """

汉诺塔实例十分经典，学习每门语言都要写一遍。

这个例子要注意：全局变量的使用以及递归的用法。递归用法注意：函数定义+分支表示。

补充

函数式编程

image.png

感觉Python很有趣，如何深入学习呢？

image.png