1. 统计学
统计学可以分为:描述统计学与推断统计学
描述统计学:使用特定的数字或图表来体现数据的集中程度和离散程度。
例:每次考试算的平均分,最高分,各个分段的人数分布等,也是属于描述统计学的范围。
推断统计学:根据样本数据推断总体数据特征。
例:产品质量检查,一般采用抽检,根据所抽样本的质量合格率作为总体的质量合格率的一个估计。
2.均值、中位数、众数、极差、方差、标准差
对于一组数组,如果只容许使用一个数字去代表这组数据,那么这个数字应该如何选择??——选择数据的中心,即反映数据集中趋势的统计量。
- 均值——算术平均数,描述平均水平。
- 中位数——将数据按大小排列后位于正中间的数描述,描述中等水平。
- 众数——数据中出现最多的数,描述一般水平。
- 极差——最大值-最小值,简单地描述数据的范围大小。
- 方差——在统计学上,更常用的是使用方差来描述数据的离散程度——数据离中心越远越离散。其中,X¡表示数据集中第i个数据的值,µ表示数据集的均值。
- 标准差——如果原数据的单位是m的话,那么方差的单位就是mˆ2,方差与原数据的单位是不一样的,两者没有可比性。为了保持单位的一致性,我们引入一个新的统计量——标准差。
2.1 均值
在统计工作中,平均数(均值)和标准差是描述数据资料集中趋势和离散程度的两个最重要的测度值。平均值有算术平均值,几何平均值,平方平均值(均方根平均值,rms),调和平均值,加权平均值等,其中以算术平均值最为常见。

其中以算术平均值最为常见,计算方法为: ;
;
几何平均值的计算方法为: ;
;
值得注意的是,几何平均值是相对于正数而言的,也就是说上面的X1,X2,..Xn必须是正数。
均方根平均值计算方法为: ;
;
调和平均值计算方法为:N/(1/x1+1/x2+…+1/xn)。
加权平均值算法为: ;
;
平均值怎么算?
计算平均值,一般常用的有两种方法:一种是简单平均法,一种是加权平均法。
例如,某企业生产A产品10台,单价100元;生产B产品5台,单价50元;生产C产品3台,单价30元,计算平均价格。
简单平均法:平均价格=∑各类产品单价/产品种类。
平均价格=(100+50+30)/3 =60(元)。
加权平均法:平均价格=∑(产品单价×产品数量)/∑(产品数量)。
平均价格=(100×10+50×5+30×3)/(10+5+3)=74.44(元)。
可以看出,简单平均与加权平均计算出来的平均值差距较大,而后者更贴近事实,属于精确计算。
2.2 中位数
顾名思义,中位数就是将数据按大小顺序(从大到小或是从小到大都可以)排列后处于中间位置的数。若处于中间位置的数据有两个(也就是数据的总个数为偶数时),中位数为中间两个数的算术平均数。
当总数个数是奇数时,按从小到大的顺序,取中间的那个数;
例:2、3、4、5、6中位数。去中间数为:4。
当总数个数是偶数时,按从小到大的顺序,取中间那两个数的平均数。
例:2、3、4、5、6、7中位数。取中间两位数为:(4+5)/2=4.5。
中位数特点
1)中位数是以它在所有标志值中所处的位置确定的全体单位标志值的代表值,不受分布数列的极大或极小值影响,从而在一定程度上提高了中位数对分布数列的代表性。
2)有些离散型变量的单项式数列,当次数分布偏态时,中位数的代表性会受到影响。
3)趋于一组有序数据的中间位置。
2.3 众数
众数——数据中出现次数最多的数(所占比例最大的数)。一组数据中,可能会存在多个众数,也可能不存在众数。众数不仅适用于数值型数据,对于非数值型数据也同样适用。
注:
1、当单项数列求众数,不需要任何计算,可以直接从分配数列中找出出现次数或频率最大的一组标志值,就是所求的众数。
2、当对组距数列求众数。那么对众数的计算有两种公式:
上限公式:
下限公式:
其中:
f 表示众数所在组次数;
f-1 表示众数所在组前一组的次数;
f+1 表示众数所在组后一组的次数;
L 表示众数所在组组距的下限;
U 表示众数所在组组距的上限;
i 表示组距。
2.4 均值、中位数、众数的优劣势
| 名称 | 优点 | 缺点 |
|---|---|---|
| 均值 | 充分利用所有数据,适用性强 | 容易受到极端值影响 |
| 中位数 | 不受极端值影响 | 缺乏敏感性 |
| 众数 | 当数据具有明显的集中趋势时,代表性好;不受极端值影响 | 缺乏唯一性:可能有一个,可能有两个,可能一个都没有 |
2.5 极差
x=xmax-xmin(xmax为最大值,xmin为最小值),极差公式是用来计算极差的最直接也是最简单的方法。有移动极差、离均差的平方和等。
极差计算公式:
x=xmax-xmin
(xmax为最大值,xmin为最小值)
方差计算公式:
s^2=(1/n)*[(x1-x0)^2+(x2-x0)^2+…+(xn-x0)^2]
(x0即为x的平均值)
2.6 方差
方差:各数据与平均数的差的平方的平均数就是方差,该公式主要用来衡量这组数据的波动大小,并把它叫做这组数据的方差,如果一组数据的方差越小,那么就证明该组数据的稳定性较高。
设一组数据x1,x2,x3……xn中,各组数据与它们的平均数x的差的平方分别是(x1-x)2,(x2-x)2……(xn-x)2,那么就可以用他们的平均数对其进行衡量,公式为:
方差公式: ;
;
方差公式经过变形后可以简化为: 。
。
方差分总体方差与样本方差。
总体方差:
样本方差:
2.7 标准差
与方差一样,标准差的值越大,表示数据越分散。有效地避免了因单位平方而引起的度量问题。
标准差:
什么是标准差:
由于方差是数据的平方,与检测值本身相差太大,人们难以直观的衡量,所以常用方差开根号换算回来这就是我们要说的标准差(SD)。
在统计学中样本的均差多是除以自由度(n-1),它的意思是样本能自由选择的程度。当选到只剩一个时,它不可能再有自由了,所以自由度是(n-1)。
标准差公式:
总体标准差=σ=sqrt(((x1-x)²+(x2-x)²+……(xn-x)²)/n)。
样本标准差=方差的算术平方根=s=sqrt(((x1-x)²+(x2-x)²+……(xn-x)²)/(n-1))。
标准差详解及示例
标准差是一组数值自平均值分散开来的程度的一种测量观念。一个较大的标准差,代表大部分的数值和其平均值之间差异较大;一个较小的标准差,代表这些数值较接近平均值。
例如,两组数的集合{0,5,9,14}和{5,6,8,9}其平均值都是7,但第二个集合具有较小的标准差。
标准差公式意义:
所有数减去其平均值的平方和,所得结果除以该组数之个数(或个数减一,即变异数),再把所得值开根号,所得之数就是这组数据的标准差。
3. 统计学直观图表
原数据太杂乱无章,难以看出规律性;只依赖数字来描述集中趋势与离散程度,让人难以对数据产生直观的印象,这时就需要用到图表。
3.1 直方图

频数分布表
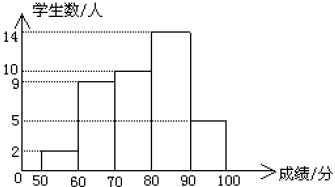 <br />**频数直方图**

频率直方图
3.2 箱线图

上边缘:除异常点以外的数据中的最大值;
上四分位数:将所有数据按照从小到大的顺序排序排在第75%位置的数字;
下四分位数:将所有数据按照从小到大的顺序排序排在第25%位置的数字;
下边缘:除异常点以外的数据中的最小值。
3.3 茎叶图
将数据分为茎和叶两部分,这里的茎是指十位上的数字,叶是指个位上的数字。将茎部分(十位)从小到大,从上到下写出来。相对于各自的茎,将同一茎(十位)的叶子(个位)从小到大,从左往右写出来。
3.4 线图

3.5 柱形图
柱形图:显示一段时间内的数据变化或显示各项之间的比较情况。
3.6 饼状图
饼状图,根据各项所占百分比决定在饼图中的扇形面积。简单易懂,通俗明了,可以更加形象地看出各个项目所占的比例大小。
4. 概率论
4.1 条件概率
已知某个事件A发生的条件下,另一个事件B发生的概率称为条件概率,记为P(B|A)。
看一下P(B|A)与P(A)、P(B)的关系:P(B|A) = P(AB) / P(A)。
条件概率也是概率的一种,所以也符合概率定义的三个条件:
- 非负性:P(B|A) ≥ 0;
- 规范性:对于必然事件S,有P(S|A) = 1;
- 可列可加性:对于两两互不相容的事件B1,B2,B3…..,即Bi · Bj = Ø,i ≠ j,i,j = 1,2,……,有P(B1 υ B2 υ …… | A) = P(B1|A) + P(B2|A) + ……
乘法定理:
由条件概率的定义,很容易得到P(AB) = P(B|A)P(A),其中P(A) > 0;
这条公式很容易推广到P(ABC) = P(C|AB)P(B|A)P(A) = P(A|BC)P(B|C)P(C).
4.2 全概率公式
设试验E的样本空间为S,A为E的一个事件,B1、B2……Bn是S的一个划分,且P(Bi) > 0 (i=1,2……n),则
在某些时候,事件A的概率不好求,但是通过全概率公式却可以很容易求得。
4.3 贝叶斯公式
设试验E的样本空间为S。A为E的一个事件,B1、B2……Bn是S的一个划分,且P(A) > 0, P(Bi) > 0 (i=1,2,…..,n),则
当对样本空间的划分由一对对立事件B与¯B组成时,全概率公式和贝叶斯公式可以简化为

贝叶斯公式的应用——诉讼、疾病诊断、垃圾邮件判别
下面来看一则案例:
病树的主人外出,委托邻居浇水,设已知如果不浇水,树死去的概率为0.8,若浇水则树死去的概率为0.15,有0.9的把握确定邻居会记得浇水。

4.4 公式比较
乘法公式、全概率公式与贝叶斯公式
- 乘法公式是求“几个事件同时发生”的概率;
- 全概率公式是求“最后结果”的概率;
- 贝叶斯公式是已知“最后结果”,求“某个事件”的概率。
先验概率与后验概率
- P(Bj|A)是在事件A发生的条件下,某个事件Bj发生的概率,称为“后验概率”;
- Bayes公式又称为“后验概率公式” 或 “逆概公式”;
- 称P(Bj)为“先验概率”。
4.5 独立性与事件
设A、B是两个事件,如果满足:P(AB) = P(A)P(B),则称事件A、B相互独立。简称A、B独立。
由事件独立的定义可以推出:
A、B独立,且P(A) > 0 ↔ P(B|A) = P(B)。
P(B|A) = P(AB)/P(A) = P(A)P(B) /P(A) = P(B)
若A、B独立,则A与¯B、¯A与¯B也相互独立。
P(A) = P(A|B)P(B) + P(A|¯B)P(¯B) = P(A)P(B) + P(A¯B)<br /> 故P(A¯B) = P(A) - P(A)P(B) = P(A)(1-P(B))=P(A)P(¯B)<br />设A、B、C是三个事件,若满足<br />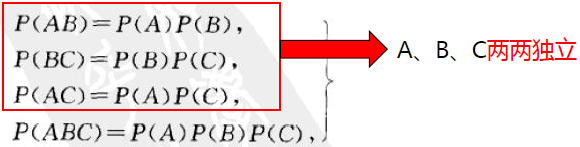<br />则称A、B、C相互独立。
4.6 相互独立事件与互斥事件、对立事件
相互独立事件:两个事件没有一点关系。
互斥事件:要么只有其中一个事件发生,要么两个事件都不发生。
对立事件:两个之中,只有一个发生。跟互斥事件相比,对立事件必然会有一个事件发生。
互斥事件与对立事件都不是相互独立事件!

