• 分享主题：Transfer Learning、Time Series
  • 论文标题：AdaRNN Adaptive Learning and Forecasting for Time Series
  • 论文链接：https://arxiv.org/pdf/2108.04443.pdf

    1.Summary

    This paper mainly studies the application of transfer learning in time series prediction. There is a covariate shift problem in machine learning. Suppose our goal is to fit y=θx. The problem now is that the distribution of x in the training set is different from that in the test set, resulting in the poor effect of θ which fits well in the training set. Corresponding this problem to the time series prediction, this paper proposes the temporal covariate shift problem. That is, if a section of time series data is divided into k sections, the distribution of x of any two sections of time series data is likely to be different. Therefore, the effect of a well trained model in one section may be very poor in the other section. The problem to be solved in this paper is to use the method based on transfer learning to solve the temporary covariate shift problem.
    In order to solve the problem of temporal covariate shift, this paper proposes an AdaRNN (adaptive RNNs) method for modeling time series, which is mainly divided into the following two steps: (1) Temporal Distribution Characterization (TDC): divide a time series into K segments, and make the distribution of x in these K segments as different as possible; (2) Temporal Distribution Matching (TDM): build a migration learning model for the above K period time series to learn a model with temporally-invariant.
    In order to deepen my understanding of this paper, I should learn more about RNN and some distribution problems (such as covariate shift).

    2.你对于论文的思考

    这篇文章中提出的AdaRNN有点类似于是用Network-based deep transfer learning（把在源域上训练好的部分网络迁移给目标域）这个方法，AdaRNN是把K个源域共同训练的一个RNN模型直接完全迁移给了目标域（因为目标域缺少标签，没办法进行训练），这个方法的创新点就在于AdaRNN里的TDM能解决temporal covariate shift问题，即解决在同一个时间序列上，不同位置的子序列段的x分布不一致的问题，这个问题解决后，那么即使训练集的分布与测试集的不同，那么也可以把这个训练完的RNN拿给测试集用，并且可以获得更好的效果。

    3. 其他

    时序预测困难的原因

    在时间序列中，时间序列数据会随着时间动态变化，特别地，时间序列的一些统计信息，如期望、方差等会随着时间动态变化，这类时间序列被称为非平稳时间序列（Non-stationary Time Series），这使得时序预测难度变大。

    解决时序预测问题的几种方法

    （1）传统方法通常基于马尔可夫假设来进行建模，即假设时间序列上的每个观测仅依赖于它的前一时刻的观测，有自回归移动平均、动态贝叶斯网络、隐马尔可夫模型等；
    （2）各种transformer类的模型；
    （3）RNN，如LSTM、GRU等模型。

    temporal covariate shift

    在机器学习中有一个covariate shift问题，假设我们的目标是要拟合y=θx，那么现在的问题是训练集的x的分布和测试集的x的分布不一样，导致在训练集上拟合的比较好的θ在测试集上效果就很差。把这个问题对应到时序预测上，本文提出了temporal covariate shift问题，即：把一段时序数据切分为K段，任意两段时序数据的x的分布很可能都是不同的，因此在某一段上训练好的模型，到了另一段上效果可能就很差了。本文就是要用基于迁移学习的方法来解决temporal covariate shift这个问题。

    AdaRNN (Adaptive RNNs)

    为了解决temporal covariate shift这个问题，本文提出了针对时间序列进行建模的AdaRNN (Adaptive RNNs)方法，主要分为如下两个步骤：
    （1）时序相似性量化(Temporal Distribution Characterization, TDC)。把一个时间序列分为K段，并且使得这K段的x的分布都互相尽量不相似，即满足以下式子：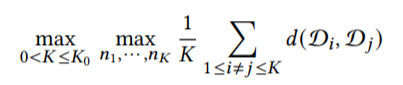
    AdaRNN Adaptive Learning and Forecasting for Time Series - 图1
    目的就是为了得到最坏的情况，如果AdaRNN能比较好的解决这么坏的情况，那么这个模型的泛化能力就会很强。
    至于切分方法，文章里使用了贪心的方法（为了提高效率而牺牲一部分切分的准确率），先把整个时间序列平均的切分为N=10段，作为后续切分为K段的最小单位。切分为K段时，先切一刀，使得当前的收益最大，然后再切下一刀，一步步局部贪心，得到最终的结果。
    （2）时序分布匹配(Temporal Distribution Matching, TDM)。模型采用了如下的RNN结构，使用了V层隐藏层。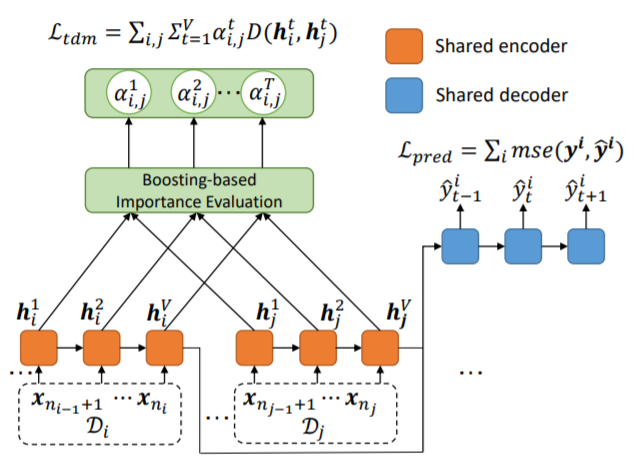
    AdaRNN Adaptive Learning and Forecasting for Time Series - 图2
    该模型的目标函数定义如下：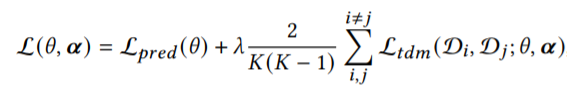
    AdaRNN Adaptive Learning and Forecasting for Time Series - 图3
    其中：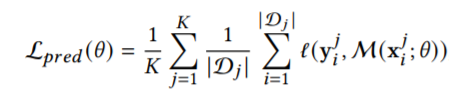
    AdaRNN Adaptive Learning and Forecasting for Time Series - 图4
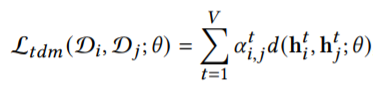
    AdaRNN Adaptive Learning and Forecasting for Time Series - 图5
    Lpred为损失函数，Ltdm是度量第i个时间序列段和第j个时间序列段的x的分布差异的函数，其中α代表了权重，初始值为1/V，由以下式子进行更新：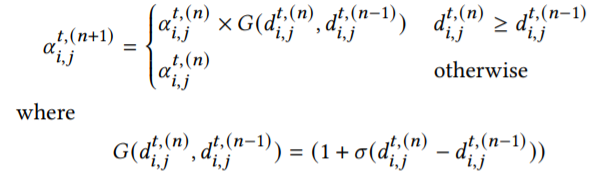
    AdaRNN Adaptive Learning and Forecasting for Time Series - 图6
    该式子表示，在第t个时间步，如果第n个轮回的d（即两个时间序列段的差异）比第n-1个轮回的d大，说明在当前这一轮（即第n+1轮），模型更应该关注这个d，加大α使得他的权重变大，否则就直接继承上一轮的α。上面式子中的σ表示sigmoid函数，意味着如果要更新α的值，那么就要将α乘上一个大于1的数（实际上是1到2之间的一个数）。
    之所以要在目标函数中加上Ltdm函数，是为了更加充分地把任意两个时间序列段的分布差异的度量加入到目标函数中（捕获RNN中每个隐藏状态的时间依赖性），使得AdaRNN能够在每一个隐藏层以及输出层的编码或解码过后，让不同时间序列段的对应的分布（隐藏层的输出、y）尽量相似，以此来解决temporal covariate shift这个问题。最终目标是，在经过AdaRNN后，不同时间序列段输出的y的分布是尽可能相似的。

    实验

    使用了四个真实数据集，包括1个分类任务(行为识别)和3个回归任务(空气质量预测、用电量预测和股价预测)。
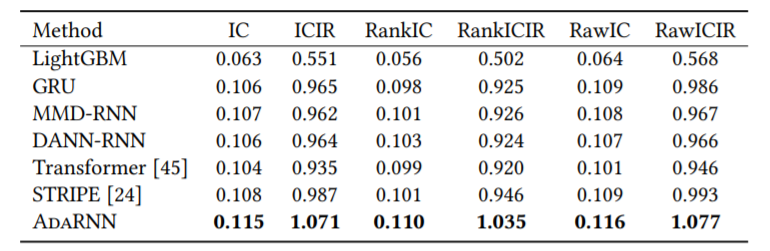
    行为识别：如下图所示，AdaRNN表现最优。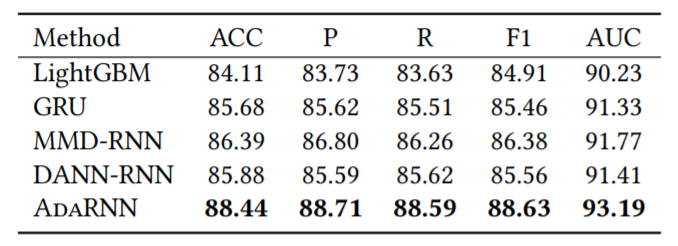
    20211214012645.png
    空气质量预测和用电量预测：如下图所示，AdaRNN表现最优。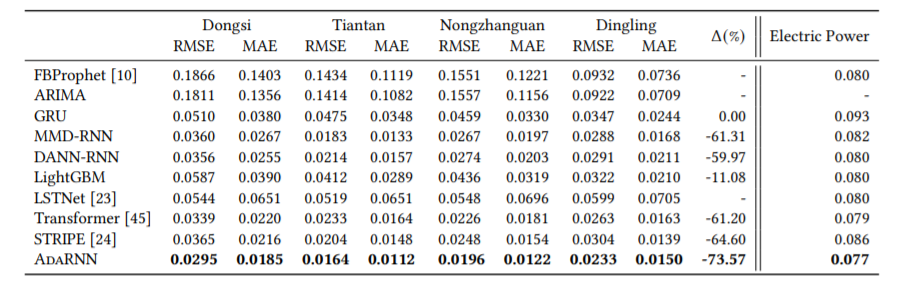
    20211214012909.png
    股价预测：如下图所示，AdaRNN表现最优。
    20211214013055.png