- 分享主题:Federated Learning
- 论文标题:Communication-Efficient Learning of Deep Networks from Decentralized Data
- 论文链接:https://arxiv.org/pdf/1602.05629.pdf
1.Summary
This is a paper about Federated learning. The paper mainly solves the problem that the data is distributed on some clients and cannot be concentrated on the data center for training. This paper proposes FederatedAveraging (FedAvg) algorithm, which can solve the problems of non-IID and unbalanced data, and protect the data from being leaked. In addition, this method also solves the problem of high model communication cost. By increasing the computation of clients in each round of training, the convergence of the model is accelerated, and the number of communication rounds between clients and server is reduced. Experiments show that the accuracy and efficiency of this method are higher than FedSGD.2.你对于论文的思考
为了让分布在许多客户端上的数据能够帮助训练模型,并且能够保护这些数据不被泄露,本文提出了FedAvg算法,它能够帮助解决联邦数据存在的诸多问题,并且能够在保持一定正确率的前提下减少通讯成本。本文的实验非常充分,主要使用了两个数据集,一个图像的,一个文本的,并用不同的方法分别划分为IID和non-IID,模型使用了2NN、CNN、LSTM这三个深度学习模型,并且在实验中尽量选择了最优的学习率,对于FedAvg的各个参数也是精心设计实验,为了验证结果,还选用了别的数据进行实验,最终得出了许多有用的结论。3. 其他
背景
移动通信设备中有许多有用的数据,利用这些数据训练模型后可以提高用户体验,但是,这些数据通常是敏感的或者很庞大的,不能直接上传到数据中心利用传统的方法训练模型。
这些来自移动通信设备中的数据具体以下特点:(1)对于模型的训练来说,这些真实数据比数据中心提供的数据更有价值;(2)这些数据是比较敏感的或较大规模的,没有必要仅因为训练模型就将其记录在数据中心;(3)对于监督任务,可以从用户交互中自然地推断出数据的标签。
例如用户手机里的照片、写手输入或者语音输入,这些数据都可以用于训练模型。
为了让这些数据能帮助模型进行训练,同时这些数据不必传到其它地方(避免泄露),本文提出了一种联邦学习的方法:FederatedAveraging(FedAvg)。联邦优化(Federated Optimization)
non-IID
集中式训练的非凸神经网络的目标函数如下(其中fi(w)是损失函数):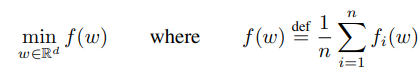
转换到联邦学习,假设数据分布在K个客户端,Dk代表客户端k数据点的集合,nk为Dk的大小,则目标函数可以表示为: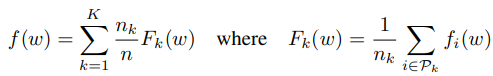
如果划分Dk是所有用户数据的随机取样,则f(w)就等价于损失函数关于Dk的期望: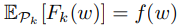
以上式子是基于用户数据独立同分布的情况,但是如果以上等式不成立,那么用户数据就是非独立同分布的(non-IID)。关键问题
联邦优化的一些关键问题:(1)用户数据是非独立同分布的(non-IID);(2)各个用户拥有的数据量是不平衡的,有的用户拥有的数据量大,有的用户拥有的数据量小;(3)用户的规模大,参与的用户多,而每个用户平均拥有的数据量小;(4)用户端设备通信限制,移动设备经常掉线,速度缓慢,费用昂贵。
除了以上问题,在实际应用中还有许多问题,如客户端数据集中的数据可能随时会添加或删除,这些实际问题都太过复杂,因此本文的实验不会考虑这些问题,但模型仍会解决non-IID、不平衡、用户端设备通信限制的问题。通信成本与计算成本
在集中式训练中,通信成本相对较小,主要是计算成本高。
在联邦优化中则相反,通信成本比较高,计算成本相对较小。
因此,我们的目标是使用额外的计算,以减少训练模型所需的通信次数,可以提高并行性,增加每个客户端的计算量(本文主要目标)。FederatedAveraging(FedAvg)
本文提出的FedAvg训练步骤如下:(1)每一轮从所有客户端中选取C-fraction个,其中C是一个比例(0<=C<=1),之后在每一个客户端上训练E次,每一次训练选取B个数据,并在客户端上更新模型参数;(2)把本轮所有参与训练的客户端的参数上传到服务器上,并根据各自的数据量加权求和,获得模型总的参数。
当B=∞时,代表选取了用户本地所有的数据。当B=∞,E=1时,就相当于FedSGD(唯一区别是FEdSGD是把梯度传到服务器上),并作为本文实验的baseline。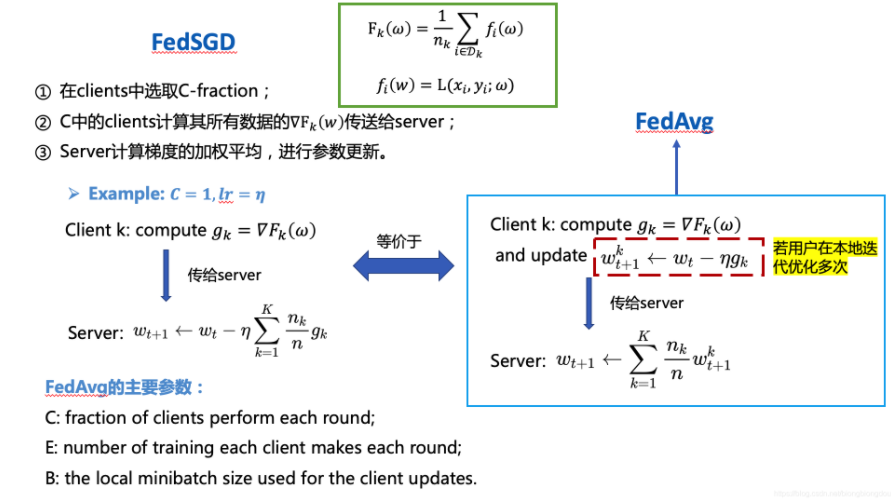
FedAvg使用的是所有客户端上的模型参数取平均值的思路,现在假设只有两个客户端,它们的模型参数分别为w1和w2,权重θ在-0.2和1.2之间,数据集使用的是MNIST数字识别,最终模型的参数取值为θw1+(1-θ)w2,下面左边是两个模型的随机初始化参数不同的情况,右边是两个模型的随机初始化参数相同的情况,可以看出,左边的平均模型明显就很差,只有在θ为0和1附近的区域效果好,说明单个模型的效果好过两个模型加权求和;右边的话在θ为0.5左右的时候效果最好,说明这是平均模型的效果是比较好的。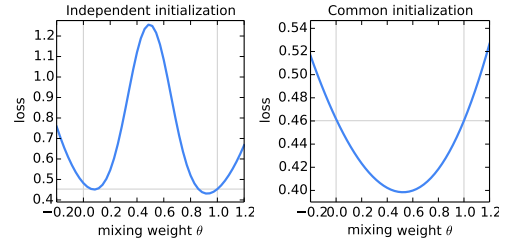
实验
数据集
(1)MINIST数字识别:手写数字0-9,一共有60000张图,数字标签是均匀的,该数据集的任务是识别数字;
(2)威廉·莎士比亚全集:用至少两行为每个剧中的每个角色构造一个数据集,一共有1146个角色,该数据基本是不平衡的,许多角色只有几行,而有些角色有很多行,该数据集的任务是读取一行中的每个字符后,预测下一个字符。模型
2NN
1.所使用的数据集:MINIST数字识别;
2.模型配置:有两个隐藏层,每个隐藏层有200个神经元,并且使用ReLu激活函数;
3.数据集划分:
(1)IID:将数据打乱,一共100个客户端,平均每个clients有600条数据;
(2)non-IID:按照数字标签(0-9)对数据进行排序,然后划分为200个大小为300的片段,然后给100个客户端都分配2个片段,也就是每个客户端有600条数据,且最多有两个数字标签的数据。CNN
1.所使用的数据集:MINIST数字识别;
2.模型配置:有两个卷积层,第一个卷积层有32个通道,第二个卷积层有64个通道,每一个通道的大小都是55,并且都使用了22的最大池化层,两个卷积层后面跟着一个有512个神经元的全连接层和ReLu激活函数,最后是一个softmax输出层;
3.数据集划分:和2NN的一样。LSTM
1.所使用的数据集:威廉·莎士比亚全集;
2.模型配置:该模型将一系列字符作为输入,并将每个字符嵌入到一个8维空间中,然后经过2个LSTM层处理,每层有256个节点,最后会经过softmax输出层。
3.数据集划分:一共有1146个角色,每一个角色分配给一个客户端,并构造了IID和non-IID两种划分方法。实验
对参数C进行实验
下表为实验结果,表中的值表示达到目标准确率(2NN的目标准确率为97%,CNN的目标准确率为99%)需要的通信轮数,在2NN中,E=1,在CNN中,E=5,表中当C=0时,表示只选取1个客户端,表中还有5个地方没有值,表示相应的模型没有在规定的时间内得到目标正确率。
可以看到,当C=0.1时,模型的收敛速度总体来看是比较好的,所有后续的实验都把C的值固定为0.1。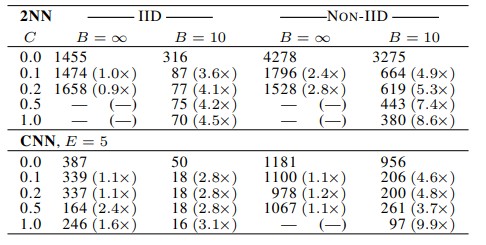
增加客户端的计算量
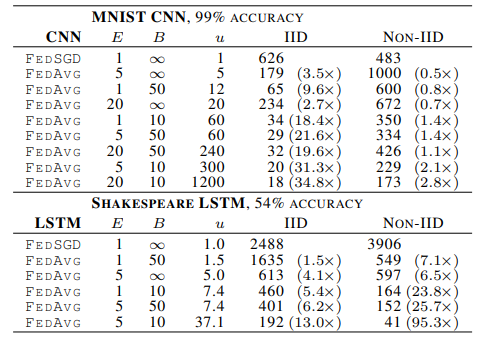
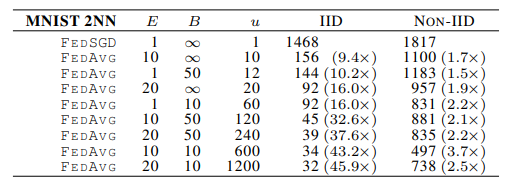
这个实验选择了2NN(只有表的数据)、CNN和LSTM(目标准确率为54%),u表示每个客户端的参数在每一轮中的期望更新次数,即u越大,客户端在每一轮中的计算量越大。
可以看到,随着u变大,通信轮数减小。
对于MNIST数字识别数据集的non-IID实验,每一个客户端分配到的数据里只有两种数字,但是实验结果显示仍然可以用FedAvg得到目标准确率,并且比baseline所需的通信轮数要少;在威廉·莎士比亚全集的non-IID实验中,客户端拥有的数据集规模是十分不平衡的,但是FedAvg不但得到了目标准确率,而且比baseline的通信轮数少非常多,这些都说明了FedAvg的鲁棒性很强。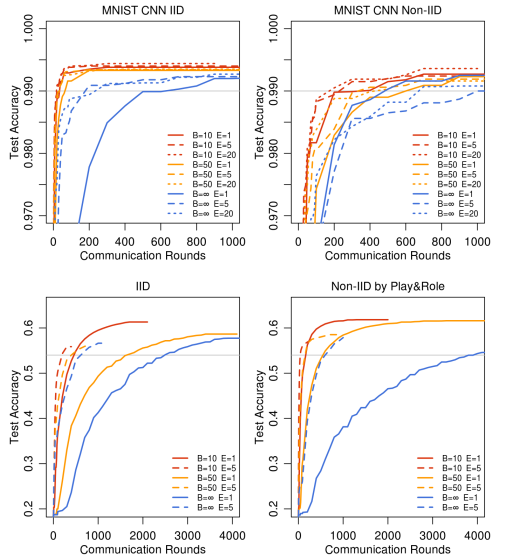
对于模型准确率的分析
对于CNN模型,FedAvg方法可以最高达到99.44%的准确率,超过baseline方法的99.22%,可能FedAvg平均过程有一定正则化的作用。对参数E进行实验
这个实验使用CNN和LSTM就进行试验,固定B=10,C=0.1,学习率也不改变,实验的目的是测试能否通过不断增加客户端在每一轮训练中的计算量,使得模型能够不断增加准确率。
对于非凸问题,模型参数的初始值就决定了这个模型最终是否会收敛到局部极小,加大E并不能使模型的准确率不断增加。

使用CIFAR-10数据集进一步进行试验
在这个实验中,FedAvg再次完胜FedSGD。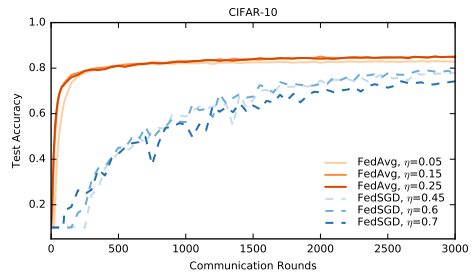

模型稳定性
如下图所示,使用了C=0的模型的准确率波动很大(绿色的线,C=0.0,E=5),而其它参数不变(除了学习率),把C调整为0.1后准确率就会稳定很多(橙色的线,C=0.0,E=5)。

