前言:求解排队问题的目的,是研究排队系统运行的效率,估计服务质量,确定系统参数的最优值,以决定系统结构是否合理、研究设计改进措施等。
一、排队系统的组成和特征
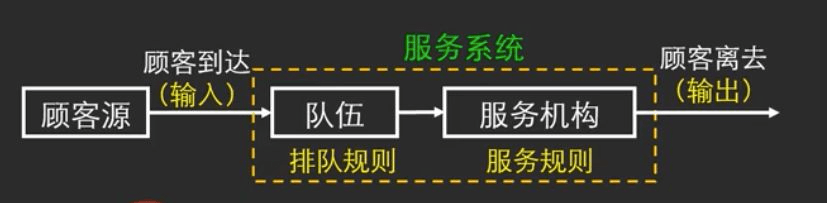
一般的排队过程都由输入过程、排队规则、服务过程三部分组成
- 输入过程
输入过程是指顾客到来时间的规律性,可能有下列不同情况:
(i)顾客的组成可能是有限的,也可能是无限的。
(ii)顾客到达的方式可能是一个一个的,也可能是成批的。
(iii)顾客到达可以是相互独立的,即以前的到达情况对以后的到达没有影响; 否则是相关的。
(iv)输入过程可以是平稳的,即相继到达的间隔时间分布及其数学期望、方差等数字特征都与时间无关,否则是非平稳的。
- 排队规则
排队规则指到达排队系统的顾客按怎样的规则排队等待,可分为损失制,等待制和 混合制三种.
(i)损失制(消失制)。当顾客到达时,所有的服务台均被占用,顾客随即离去。
(ii)等待制。当顾客到达时,所有的服务台均被占用,顾客就排队等待,直到接受完服务才离去。例如出故障的机器排队等待维修就是这种情况。
排队方式还分为单列、多列和循环队列。
- 服务过程
(i)服务机构。主要有以下几种类型:单服务台;多服务台并联(每个服务台同 时为不同顾客服务);多服务台串联(多服务台依次为同一顾客服务);混合型。
(ii)服务规则。按为顾客服务的次序采用以下几种规则:
①先到先服务,这是通常的情形。
②后到先服务,如情报系统中,后到的情报信息往往有价值,因而常被优先处理。
③随机服务,服务台从等待的顾客中随机地取其一进行服务,而不管到达的先后。
④优先服务,如医疗系统对病情严重的病人给予优先治疗。
二、符号概念与记法
X/Y/Z/A/B/C
- X:表示相继到达间隔时间的分布;
- Y:表示服务时间的分布;
- Z:并列的服务台的数目;
- A:系统容量(队长);
- B:系统状态(顾客源数);
- C:服务规则

- 常用指标:
- 队长(系统内顾客数)
和排队长(排队等候顾客数)
,系统内顾客数=排队等候顾客数+正在接受服务的顾客数
- 逗留时间(系统内总时间)
和等待时间(排队时间)
- 忙期、损失率、服务强度等
基本概念:
(1)泊松分布(最简单流):t时段内有k个顾客来到服务系统的概率 服从泊松分布,其中
表示单位时间内随机事件平均发生次数,即平均到达率。
其满足三个条件:①无后效性;②平稳性;③普通性
(2)负指数分布:用 表示依次服务完毕离去的顾客的间隔时间
的概率密度函数,
用 表示
的概率分布函数。
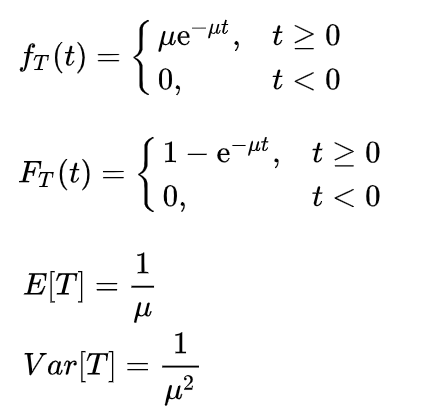
重要性质——无记忆性或马尔科夫性,假设每个顾客的服务时间服从负指数分布,则 表示单位时间能被服务完成的顾客数,称为平均服务率。

(3)k阶爱尔朗分布:K个相互独立具有相同参数的负指数分布的和的分布,称为k阶爱尔朗分布。
- 如:k个串列的服务台,k道工序。k个随机变量,服从参数
的负指数分布,
即 其概率密度、期望、方差:
服务强度 ,平均到达率和平均服务率之比。
三、实际问题对应模型
,标准单服务台排队模型,例:医生手术
,系统容量有限的情况,例:理发店
,顾客源有限的情况,例:车间机器维修
,标准多服务台排队模型,例:多窗口售票
,顾客源有限,多服务台排队系统,例:多工人的车间机器维修
,系统容量有限,多服务台排队系统。例:民宿房间数
*指标计算公式(应用时对应查找)
以定长服务时间模型和爱尔朗服务时间模型为例:**
下面主要考虑静态问题的优化
- M/M/1模型的最优服务率,
的优化。
例:目标函数 表示服务成本和等待成本之和的期望,
,其中
表示单位时间服务的人均成本,
表示顾客单位时间停留成本。
- M/M/c模型的最优服务台数,
的优化。
例:目标函数 是总费用的期望,
,其中
表示每服务台单位时间成本,
同上

